2280

2280. Minimum Lines to Represent a Line Chart (Medium)

You are given a 2D integer array stockPrices where stockPrices[i] = [dayi, pricei] indicates the price of the stock on day dayi is pricei. A line chart is created from the array by plotting the points on an XY plane with the X-axis representing the day and the Y-axis representing the price and connecting adjacent points. One such example is shown below:

Return the minimum number of lines needed to represent the line chart.

 

Example 1:

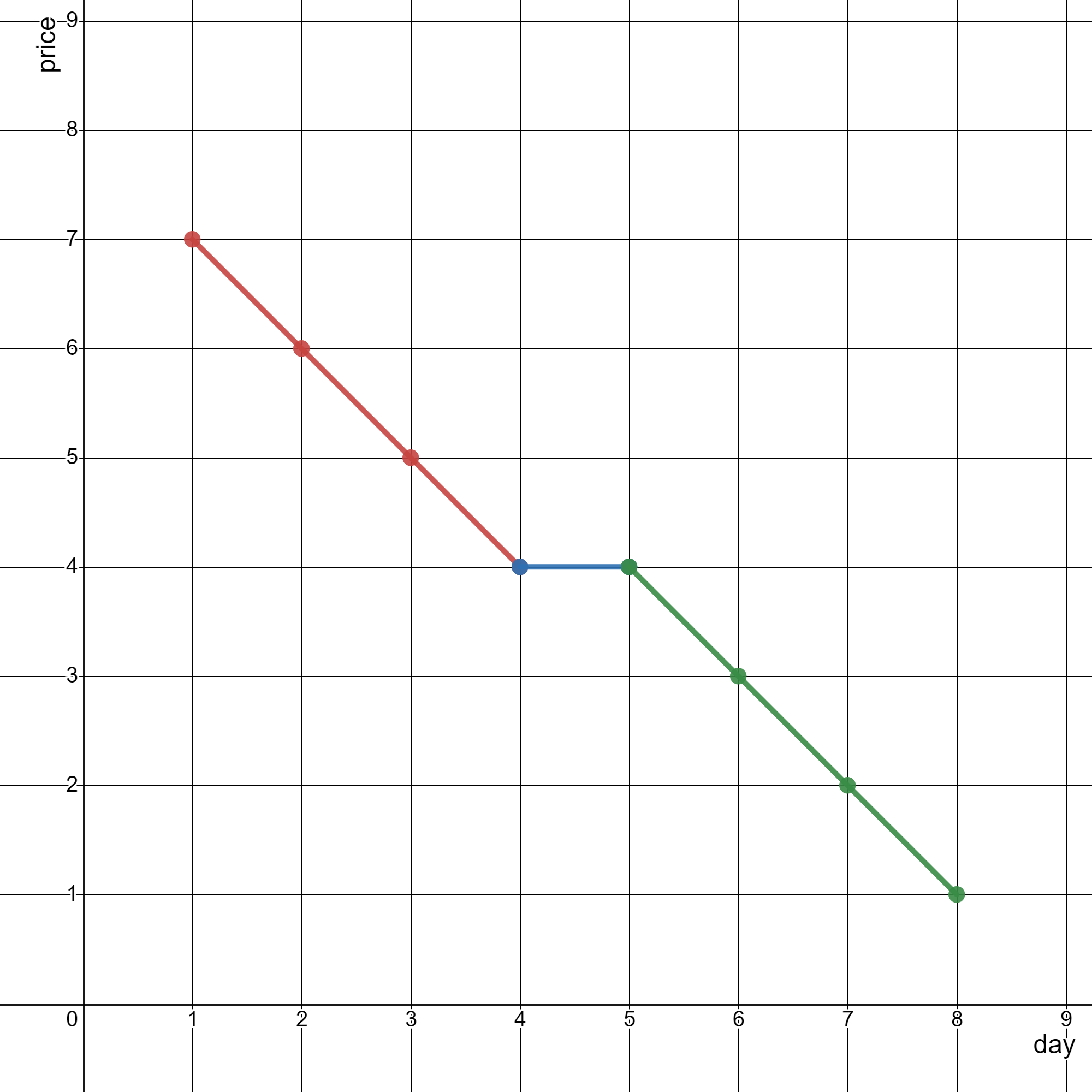
Input: stockPrices = [[1,7],[2,6],[3,5],[4,4],[5,4],[6,3],[7,2],[8,1]]
Output: 3
Explanation:
The diagram above represents the input, with the X-axis representing the day and Y-axis representing the price.
The following 3 lines can be drawn to represent the line chart:
- Line 1 (in red) from (1,7) to (4,4) passing through (1,7), (2,6), (3,5), and (4,4).
- Line 2 (in blue) from (4,4) to (5,4).
- Line 3 (in green) from (5,4) to (8,1) passing through (5,4), (6,3), (7,2), and (8,1).
It can be shown that it is not possible to represent the line chart using less than 3 lines.

Example 2:

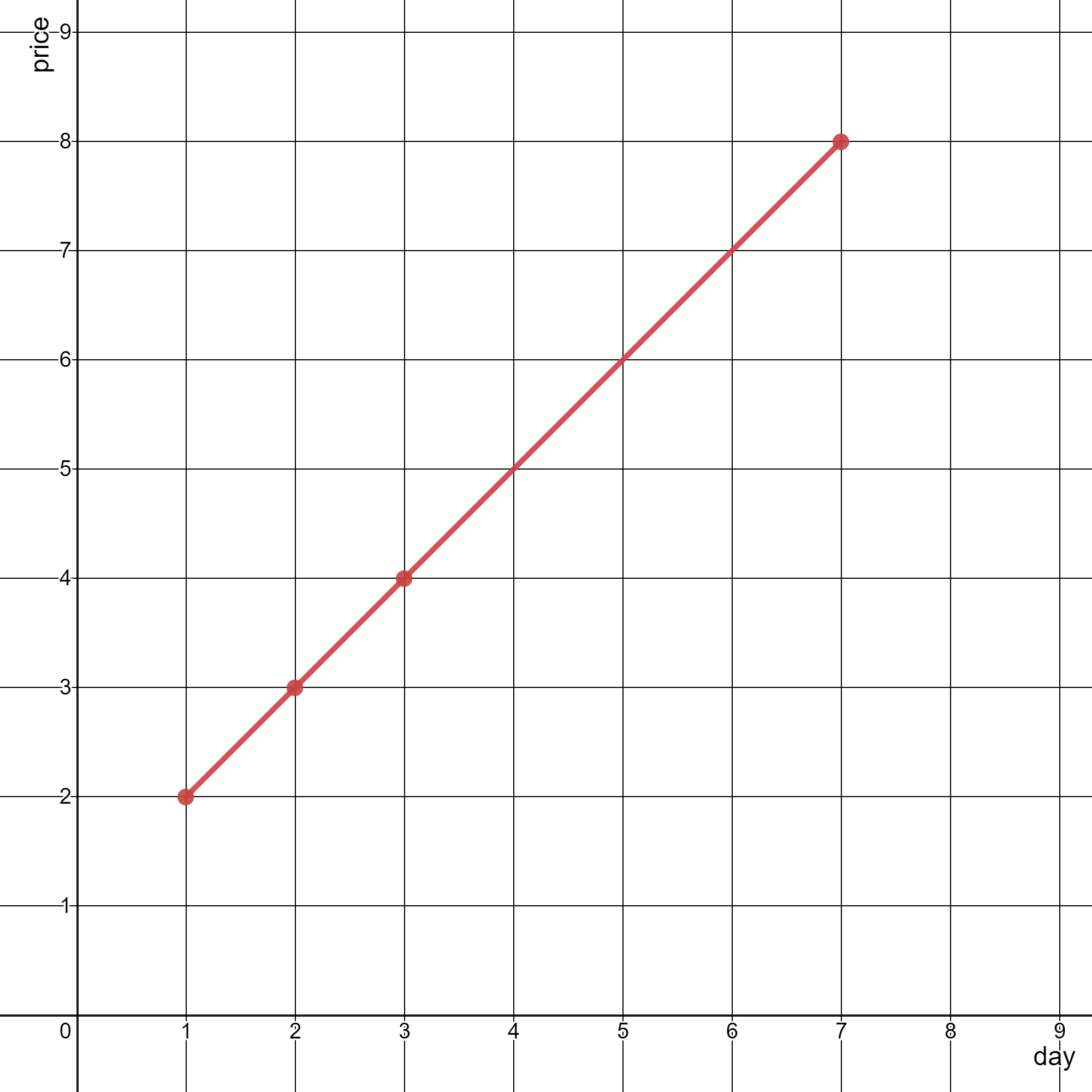
Input: stockPrices = [[3,4],[1,2],[7,8],[2,3]]
Output: 1
Explanation:
As shown in the diagram above, the line chart can be represented with a single line.

 

Constraints:

• 1 <= stockPrices.length <= 105
• stockPrices[i].length == 2
• 1 <= dayi, pricei <= 109
• All dayi are distinct.

Companies: Google

Related Topics:
Array, Math, Geometry, Sorting, Number Theory

Similar Questions:

• Max Points on a Line (Hard)
• Minimum Number of Lines to Cover Points (Medium)

Hints:

• When will three adjacent points lie on the same line? How can we generalize this for all points?
• Will calculating the slope of lines connecting adjacent points help us find the answer?

Solution 1.

// OJ: https://leetcode.com/problems/minimum-lines-to-represent-a-line-chart
// Author: github.com/lzl124631x
// Time: O(NlogN)
// Space: O(1)
class Solution {
public:
    int minimumLines(vector<vector<int>>& A) {
        int N = A.size(), ans = N - 1;
        sort(begin(A), end(A));
        auto sameLine = [&](int i, int j, int k) {
            return (long)(A[j][1] - A[i][1]) * (A[k][0] - A[j][0]) == (long)(A[k][1] - A[j][1]) * (A[j][0] - A[i][0]);
        };
        for (int i = 2; i < N; ++i) {
            if (sameLine(i - 2, i - 1, i)) --ans;
        }
        return ans;
    }
};