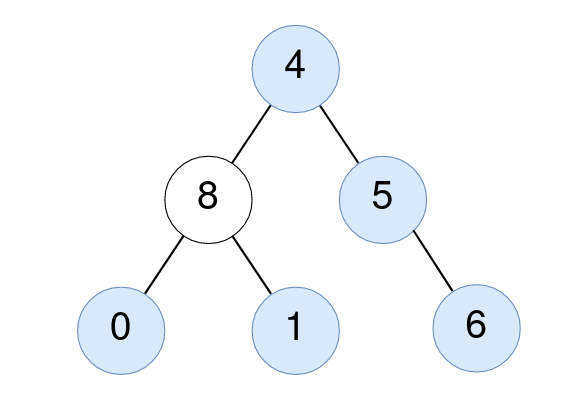
Given the root of a binary tree, return the number of nodes where the value of the node is equal to the average of the values in its subtree.
Note:
- The average of
nelements is the sum of thenelements divided bynand rounded down to the nearest integer. - A subtree of
rootis a tree consisting ofrootand all of its descendants.
Example 1:
Input: root = [4,8,5,0,1,null,6] Output: 5 Explanation: For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4. For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5. For the node with value 0: The average of its subtree is 0 / 1 = 0. For the node with value 1: The average of its subtree is 1 / 1 = 1. For the node with value 6: The average of its subtree is 6 / 1 = 6.
Example 2:
Input: root = [1] Output: 1 Explanation: For the node with value 1: The average of its subtree is 1 / 1 = 1.
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. 0 <= Node.val <= 1000
Companies: Google, Facebook, Amazon
Related Topics:
Tree, Depth-First Search, Binary Tree
Similar Questions:
- Maximum Average Subtree (Medium)
- Insufficient Nodes in Root to Leaf Paths (Medium)
- Count Nodes Equal to Sum of Descendants (Medium)
Hints:
- What information do we need to calculate the average? We need the sum of the values and the number of values.
- Create a recursive function that returns the size of a node’s subtree, and the sum of the values of its subtree.
// OJ: https://leetcode.com/problems/count-nodes-equal-to-average-of-subtree
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(H)
class Solution {
int ans = 0;
pair<int, int> dfs(TreeNode *root) {
if (!root) return {0,0};
auto [lc, ls] = dfs(root->left);
auto [rc, rs] = dfs(root->right);
ans += root->val == (root->val + ls + rs) / (1 + lc + rc);
return {lc + rc + 1, ls + rs + root->val};
}
public:
int averageOfSubtree(TreeNode* root) {
dfs(root);
return ans;
}
};