2128

2128. Remove All Ones With Row and Column Flips (Medium)

You are given an m x n binary matrix grid.

In one operation, you can choose any row or column and flip each value in that row or column (i.e., changing all 0's to 1's, and all 1's to 0's).

Return true if it is possible to remove all 1's from grid using any number of operations or false otherwise.

 

Example 1:

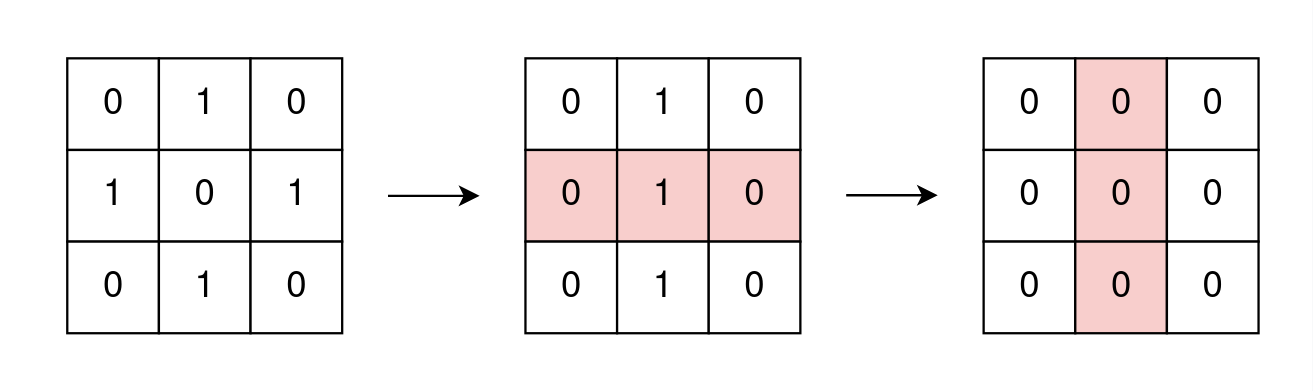
Input: grid = [[0,1,0],[1,0,1],[0,1,0]]
Output: true
Explanation: One possible way to remove all 1's from grid is to:
- Flip the middle row
- Flip the middle column

Example 2:

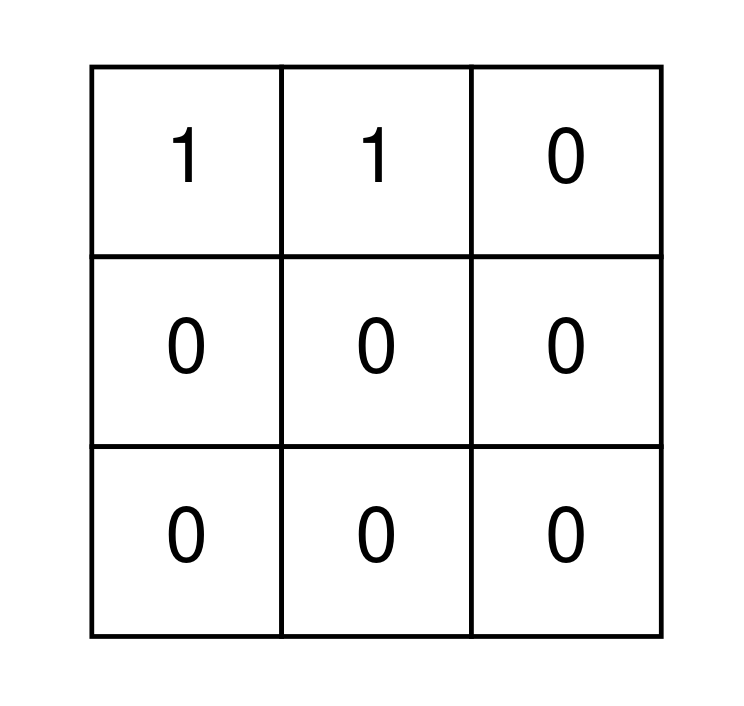
Input: grid = [[1,1,0],[0,0,0],[0,0,0]]
Output: false
Explanation: It is impossible to remove all 1's from grid.

Example 3:

Input: grid = [[0]]
Output: true
Explanation: There are no 1's in grid.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• grid[i][j] is either 0 or 1.

Companies:
Google

Related Topics:
Array, Math, Bit Manipulation, Matrix

Similar Questions:

• Score After Flipping Matrix (Medium)
• Minimum Number of Flips to Convert Binary Matrix to Zero Matrix (Hard)
• Minimum Operations to Remove Adjacent Ones in Matrix (Hard)

Solution 1.

// OJ: https://leetcode.com/problems/remove-all-ones-with-row-and-column-flips/
// Author: github.com/lzl124631x
// Time: O(MN)
// Space: O(1)
class Solution {
public:
    bool removeOnes(vector<vector<int>>& A) {
        int M = A.size(), N = A[0].size();
        for (int i = 0; i < M; ++i) {
            if (A[i][0] == 0) continue;
            for (int j = 0; j < N; ++j) A[i][j] = 1 - A[i][j];
        }
        for (int j = 0; j < N; ++j) {
            if (A[0][j] == 0) continue;
            for (int i = 0; i < M; ++i) {
                A[i][j] = 1 - A[i][j];
            }
        }
        for (int i = 0; i < M; ++i) {
            for (int j = 0; j < N; ++j) {
                if (A[i][j]) return false;
            }
        }
        return true;
    }
};

Solution 2.

// OJ: https://leetcode.com/problems/remove-all-ones-with-row-and-column-flips/
// Author: github.com/lzl124631x
// Time: O(MN)
// Space: O(1)
class Solution {
public:
    bool removeOnes(vector<vector<int>>& A) {
        int M = A.size(), N = A[0].size();
        for (int i = 0; i < M; ++i) {
            if (A[i][0]) {
                for (int j = 0; j < N; ++j) A[i][j] = 1 - A[i][j];
            }
            if (i > 0) {
                for (int j = 0; j < N; ++j) {
                    if (A[i][j] != A[0][j]) return false;
                }
            }
        }
        return true;
    }
};