2090

2090. K Radius Subarray Averages (Medium)

You are given a 0-indexed array nums of n integers, and an integer k.

The k-radius average for a subarray of nums centered at some index i with the radius k is the average of all elements in nums between the indices i - k and i + k (inclusive). If there are less than k elements before or after the index i, then the k-radius average is -1.

Build and return an array avgs of length n where avgs[i] is the k-radius average for the subarray centered at index i.

The average of x elements is the sum of the x elements divided by x, using integer division. The integer division truncates toward zero, which means losing its fractional part.

• For example, the average of four elements 2, 3, 1, and 5 is (2 + 3 + 1 + 5) / 4 = 11 / 4 = 3.75, which truncates to 3.

 

Example 1:

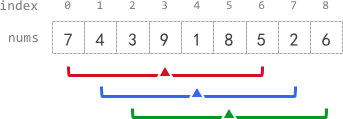
Input: nums = [7,4,3,9,1,8,5,2,6], k = 3
Output: [-1,-1,-1,5,4,4,-1,-1,-1]
Explanation:
- avg[0], avg[1], and avg[2] are -1 because there are less than k elements before each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
  Using integer division, avg[3] = 37 / 7 = 5.
- For the subarray centered at index 4, avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg[6], avg[7], and avg[8] are -1 because there are less than k elements after each index.

Example 2:

Input: nums = [100000], k = 0
Output: [100000]
Explanation:
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
  avg[0] = 100000 / 1 = 100000.

Example 3:

Input: nums = [8], k = 100000
Output: [-1]
Explanation: 
- avg[0] is -1 because there are less than k elements before and after index 0.

 

Constraints:

• n == nums.length
• 1 <= n <= 105
• 0 <= nums[i], k <= 105

Similar Questions:

• Minimum Size Subarray Sum (Medium)
• Moving Average from Data Stream (Easy)
• Subarray Sum Equals K (Medium)
• Maximum Average Subarray I (Easy)
• Number of Sub-arrays of Size K and Average Greater than or Equal to Threshold (Medium)

Solution 1. Sliding Window

Intuition: Keep a fixed-length sliding window of length 2k + 1. Slide it from left to right, and update the sum of the window on the fly.

Algorithm:

Let len = 2*k + 1.

If N < len, return all -1s directly because this array is too short to cover any window

Otherwise, loop i from 0 to N-1:

• Push A[i] into the window. sum += A[i]
• Pop A[i-len] out of the window. sum -= A[i - len]
• Assign the average value. ans[i - k] = sum / len.

// OJ: https://leetcode.com/problems/k-radius-subarray-averages/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(1) extra space
class Solution {
public:
    vector<int> getAverages(vector<int>& A, int k) {
        long N = A.size(), len = 2 * k + 1, sum = 0; // `len` is the length of the window
        vector<int> ans(N, -1);
        if (N < len) return ans; // If the array is too short to cover a window, return all -1s
        for (int i = 0; i < N; ++i) {
            sum += A[i]; // push A[i] into the window
            if (i - len >= 0) sum -= A[i - len]; // pop A[i-len], if any, out of window
            if (i >= len - 1) ans[i - k] = sum / len; // the center of this window is at `i-k`
        }
        return ans;
    }
};

Solution 2. Prefix Sum

// OJ: https://leetcode.com/problems/k-radius-subarray-averages/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
class Solution {
public:
    vector<int> getAverages(vector<int>& A, int k) {
        int N = A.size(), len = 2 * k + 1;
        vector<int> ans(N, -1);
        if (N < len) return ans; // If the array is too short to cover a window, return all -1s
        vector<long> sum(N + 1);
        for (int i = 0; i < N; ++i) sum[i + 1] = sum[i] + A[i];
        for (int i = k; i + k < N; ++i) ans[i] = (sum[i + k + 1] - sum[i - k]) / len;
        return ans;
    }
};

Discuss

https://leetcode.com/problems/k-radius-subarray-averages/discuss/1599803/C%2B%2B-O(N)-time-Sliding-Window