1975

1975. Maximum Matrix Sum (Medium)

You are given an n x n integer matrix. You can do the following operation any number of times:

• Choose any two adjacent elements of matrix and multiply each of them by -1.

Two elements are considered adjacent if and only if they share a border.

Your goal is to maximize the summation of the matrix's elements. Return the maximum sum of the matrix's elements using the operation mentioned above.

 

Example 1:

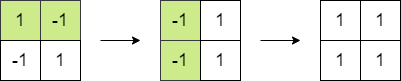
Input: matrix = [[1,-1],[-1,1]]
Output: 4
Explanation: We can follow the following steps to reach sum equals 4:
- Multiply the 2 elements in the first row by -1.
- Multiply the 2 elements in the first column by -1.

Example 2:

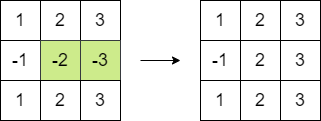
Input: matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]
Output: 16
Explanation: We can follow the following step to reach sum equals 16:
- Multiply the 2 last elements in the second row by -1.

 

Constraints:

• n == matrix.length == matrix[i].length
• 2 <= n <= 250
• -105 <= matrix[i][j] <= 105

Solution 1. Brain Teaser + Greedy

If there are even number of negative numbers, we can make all of them positive.

If there are odd number of negative numbers, we can leave one number negative. We can greedily pick the number with the smallest absolute value.

// OJ: https://leetcode.com/problems/maximum-matrix-sum/
// Author: github.com/lzl124631x
// Time: O(N^2)
// Space: O(1)
class Solution {
public:
    long long maxMatrixSum(vector<vector<int>>& A) {
        long long cnt = 0, sum = 0, N = A.size(), mn = INT_MAX;
        for (int i = 0; i < N; ++i) {
            for (int j = 0; j < N; ++j) {
                cnt += A[i][j] < 0;
                sum += abs(A[i][j]);
                mn = min(mn, (long long)abs(A[i][j]));
            }
        }
        return cnt % 2 ? sum - 2 * mn : sum;
    }
};