Skip to content

Latest commit

 

History

History

1786

Folders and files

NameName
Last commit message
Last commit date

parent directory

..
README.md
README.md
 
 

README.md

1786. Number of Restricted Paths From First to Last Node (Medium)

There is an undirected weighted connected graph. You are given a positive integer n which denotes that the graph has n nodes labeled from 1 to n, and an array edges where each edges[i] = [ui, vi, weighti] denotes that there is an edge between nodes ui and vi with weight equal to weighti.

A path from node start to node end is a sequence of nodes [z0, z1, z2, ..., zk] such that z0 = start and zk = end and there is an edge between zi and zi+1 where 0 <= i <= k-1.

The distance of a path is the sum of the weights on the edges of the path. Let distanceToLastNode(x) denote the shortest distance of a path between node n and node x. A restricted path is a path that also satisfies that distanceToLastNode(zi) > distanceToLastNode(zi+1) where 0 <= i <= k-1.

Return the number of restricted paths from node 1 to node n. Since that number may be too large, return it modulo 109 + 7.

 

Example 1:

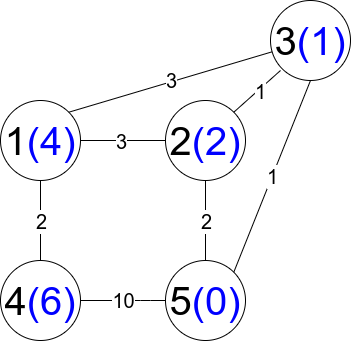
Input: n = 5, edges = [[1,2,3],[1,3,3],[2,3,1],[1,4,2],[5,2,2],[3,5,1],[5,4,10]]
Output: 3
Explanation: Each circle contains the node number in black and its distanceToLastNode value in blue. The three restricted paths are:
1) 1 --> 2 --> 5
2) 1 --> 2 --> 3 --> 5
3) 1 --> 3 --> 5

Example 2:

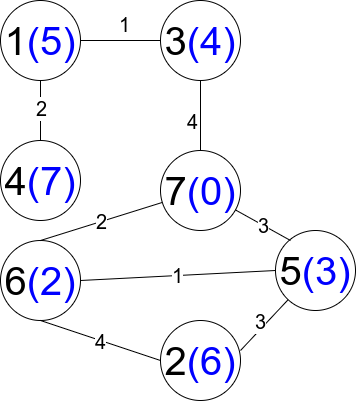
Input: n = 7, edges = [[1,3,1],[4,1,2],[7,3,4],[2,5,3],[5,6,1],[6,7,2],[7,5,3],[2,6,4]]
Output: 1
Explanation: Each circle contains the node number in black and its distanceToLastNode value in blue. The only restricted path is 1 --> 3 --> 7.

 

Constraints:

  • 1 <= n <= 2 * 104
  • n - 1 <= edges.length <= 4 * 104
  • edges[i].length == 3
  • 1 <= ui, vi <= n
  • ui != vi
  • 1 <= weighti <= 105
  • There is at most one edge between any two nodes.
  • There is at least one path between any two nodes.

Companies:
Google

Related Topics:
Dynamic Programming, Graph, Topological Sort, Heap (Priority Queue), Shortest Path

Similar Questions:

Solution 1. Dijkstra + DP

We run Dijkstra algorithm starting from the nth node.

Let dist[u] be the distance from the u node to nth node.

Let cnt[u] be the number of restricted path from u node to nth node.

Each time we visit a new node u, we can update its cnt[u] to be the sum of cnt[v] where v is a neighbor of u and dist[v] is smaller than dist[u].

The answer is cnt[0].

// OJ: https://leetcode.com/problems/number-of-restricted-paths-from-first-to-last-node/
// Author: github.com/lzl124631x
// Time: O(ElogE)
// Space: O(E)
class Solution {
    typedef pair<int, int> PII;
public:
    int countRestrictedPaths(int n, vector<vector<int>>& E) {
        long mod = 1e9 + 7;
        vector<vector<PII>> G(n);
        for (auto &e : E) {
            int u = e[0] - 1, v = e[1] - 1, w = e[2];
            G[u].emplace_back(v, w);
            G[v].emplace_back(u, w);
        }
        priority_queue<PII, vector<PII>, greater<PII>> pq;
        vector<long> dist(n, INT_MAX), cnt(n, 0);
        dist[n - 1] = 0;
        cnt[n - 1] = 1;
        pq.emplace(0, n - 1);
        while (pq.size()) {
            auto [cost, u] = pq.top();
            pq.pop();
            if (cost > dist[u]) continue;
            for (auto &[v, w] : G[u]) {
                if (dist[v] > cost + w) {
                    dist[v] = cost + w;
                    pq.emplace(dist[v], v);
                }
                if (cost > dist[v]) cnt[u] = (cnt[u] + cnt[v]) % mod;
            }
        }
        return cnt[0];
    }
};