1739

1739. Building Boxes (Hard)

You have a cubic storeroom where the width, length, and height of the room are all equal to n units. You are asked to place n boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:

• You can place the boxes anywhere on the floor.
• If box x is placed on top of the box y, then each side of the four vertical sides of the box y must either be adjacent to another box or to a wall.

Given an integer n, return the minimum possible number of boxes touching the floor.

 

Example 1:

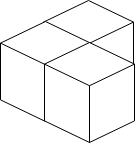
Input: n = 3
Output: 3
Explanation: The figure above is for the placement of the three boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.

Example 2:

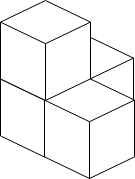
Input: n = 4
Output: 3
Explanation: The figure above is for the placement of the four boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.

Example 3:

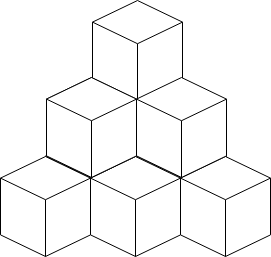
Input: n = 10
Output: 6
Explanation: The figure above is for the placement of the ten boxes.
These boxes are placed in the corner of the room, where the corner is on the back side.

 

Constraints:

• 1 <= n <= 109

Related Topics:
Math, Binary Search

Solution 1.

We need to build the pyramid at the corner of the walls.

Let "complete pyramid" be the pyramid with the smallest n to reach height h.

For example, n = 1, 4, 10, ... forms complete pyramid.

The bottom layer of complete pyramid:

height    bottom
1         1
2         1 + 2 = 3
3         1 + 2 + 3 = 6
4         1 + 2 + 3 + 4 = 10
5         1 + 2 + 3 + 4 + 5 = 15
...

bottom(h) = (1 + h) * h / 2
bottom(1) = 1

The number of cubes in complete pyramids:

height    total
1         1
2         1 + 3 = 4
3         4 + 6 = 10
4         10 + 10 = 20
5         20 + 15 = 35
...

total(h) = total(h - 1) + bottom(h)
total(1) = 1

The first step is to find the greatest h that total(h) <= n. We can get this using iteration.

Assume it's H, then we have n - total(H) remaining cubes to place. We need to put them from the floor then build upwards.

For height H, we can place at most H + 1 remaining cubes on the floor, the rest will be placed at other layers.

Take H = 4 for example, we can at most place 5 cubes on the floor.

We place the remaining cubes in this order

        (15)
      (10) (14)
    (6) (9) (13)
  (3) (5) (8) (12)
(1) (2) (4) (7) (11)

The breakpoints are 1, 3, 6, 10, 15 which are 1, 1+2, 1+2+3, 1+2+3+4, 1+2+3+4+5.

So if we have k cubes on floor, we at most can hold f(k) = (1 + k) * k / 2 remaing cubes.

We know the number of remaining cubes r, and we need to get the smallest k that f(k) >= r (0 <= k <= H + 1).

We can get this using binary search.

// OJ: https://leetcode.com/problems/building-boxes/
// Author: github.com/lzl124631x
class Solution {
public:
    int minimumBoxes(int n) {
        int bottom = 1, total = 1, h = 1;
        while (total + bottom + h + 1 <= n) {
            bottom += ++h;
            total += bottom;
        }
        int r = n - total, L = 0, R = h + 1;
        while (L <= R) {
            int M = (L + R) / 2;
            if ((1 + M) * M / 2 >= r) R = M - 1;
            else L = M + 1;
        }
        return bottom + L;
    }
};

Solution 2.

bottom(h) = (1 + h) * h / 2 = (h + h^2) / 2
total(h) = bottom(1) + bottom(2) + ... + bottom(h)
         = (1 + 2 + ... + h) / 2 + (1^2 + 2^2 + ... + h^2) / 2
         = (1 + h) * h / 4 + h * (h + 1) * (2h + 1) / 12 
         = h / 12 * (3 * (1 + h) + (h + 1) * (2h + 1))
         = h / 12 * (1 + h) * (2h + 4)
         = h * (h + 1) * (h + 2) / 6

So we can use this equation to find the greatest h that total(h) <= n.

// OJ: https://leetcode.com/problems/building-boxes/
// Author: github.com/lzl124631x
class Solution {
public:
    int minimumBoxes(int n) {
        auto cube = [](int h) { return (long)h * (h + 1) * (h + 2) / 6; };
        auto getHeight = [&](int n) {
            long L = 1, R = 1e5;
            while (L <= R) {
                long M = (L + R) / 2;
                if (cube(M) <= n) L = M + 1;
                else R = M - 1;
            }
            return R;
        };
        int h = getHeight(n), total = cube(h), bottom = (1 + h) * h / 2;
        int r = n - total, L = 0, R = h + 1;
        while (L <= R) {
            int M = (L + R) / 2;
            if ((1 + M) * M / 2 >= r) R = M - 1;
            else L = M + 1;
        }
        return bottom + L;
    }
};