1601

1601. Maximum Number of Achievable Transfer Requests (Hard)

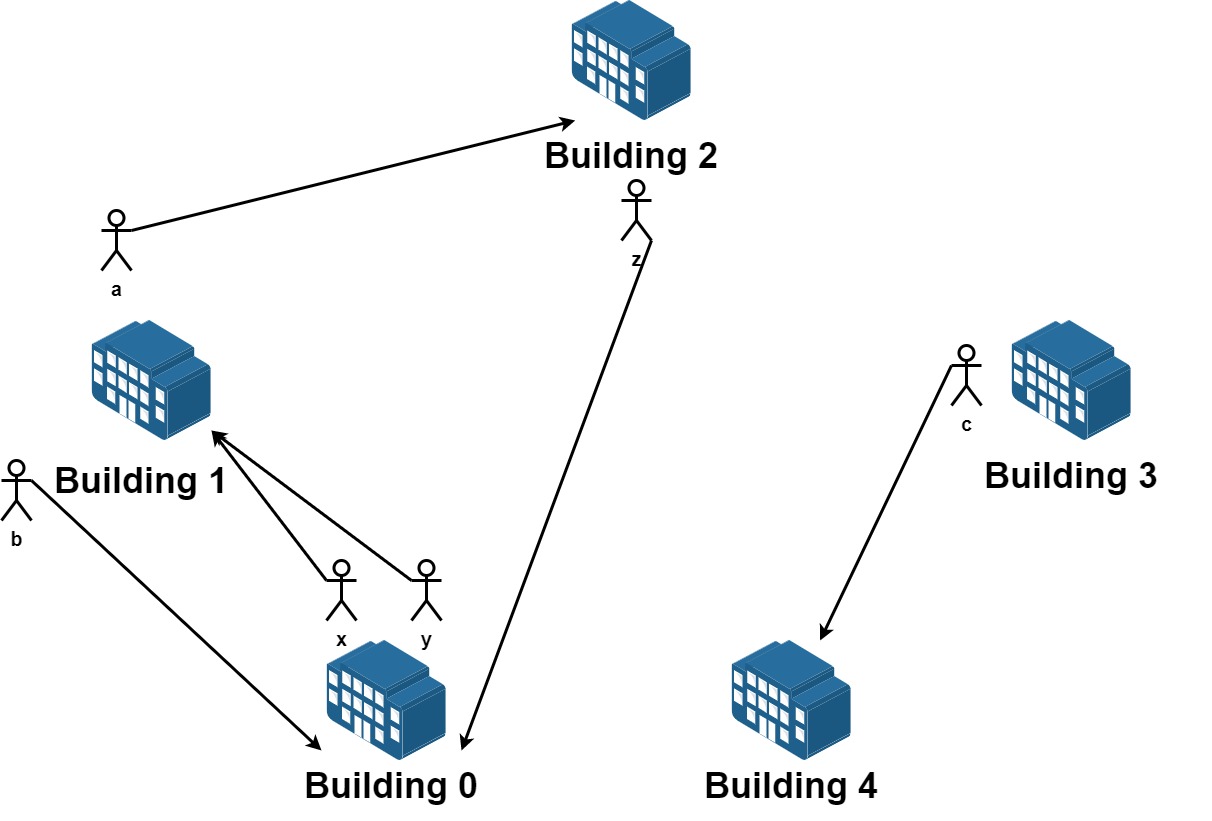
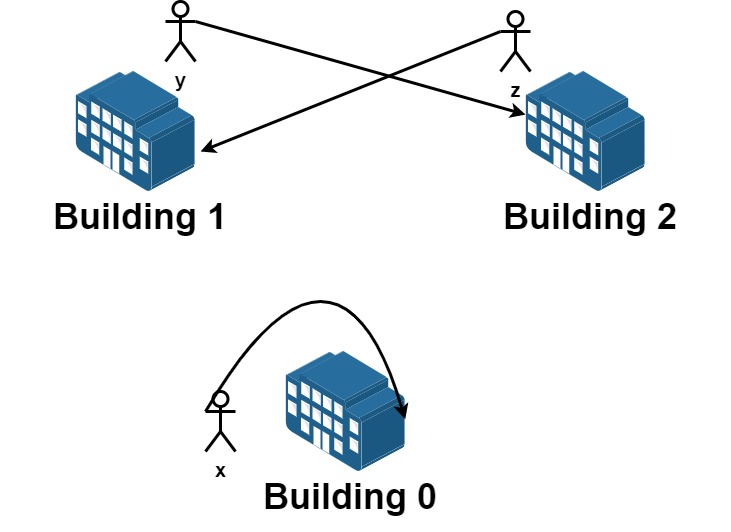
We have n buildings numbered from 0 to n - 1. Each building has a number of employees. It's transfer season, and some employees want to change the building they reside in.

You are given an array requests where requests[i] = [fromi, toi] represents an employee's request to transfer from building fromi to building toi.

All buildings are full, so a list of requests is achievable only if for each building, the net change in employee transfers is zero. This means the number of employees leaving is equal to the number of employees moving in. For example if n = 3 and two employees are leaving building 0, one is leaving building 1, and one is leaving building 2, there should be two employees moving to building 0, one employee moving to building 1, and one employee moving to building 2.

Return the maximum number of achievable requests.

 

Example 1:

Input: n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
Output: 5
Explantion: Let's see the requests:
From building 0 we have employees x and y and both want to move to building 1.
From building 1 we have employees a and b and they want to move to buildings 2 and 0 respectively.
From building 2 we have employee z and they want to move to building 0.
From building 3 we have employee c and they want to move to building 4.
From building 4 we don't have any requests.
We can achieve the requests of users x and b by swapping their places.
We can achieve the requests of users y, a and z by swapping the places in the 3 buildings.

Example 2:

Input: n = 3, requests = [[0,0],[1,2],[2,1]]
Output: 3
Explantion: Let's see the requests:
From building 0 we have employee x and they want to stay in the same building 0.
From building 1 we have employee y and they want to move to building 2.
From building 2 we have employee z and they want to move to building 1.
We can achieve all the requests. 

Example 3:

Input: n = 4, requests = [[0,3],[3,1],[1,2],[2,0]]
Output: 4

 

Constraints:

• 1 <= n <= 20
• 1 <= requests.length <= 16
• requests[i].length == 2
• 0 <= fromi, toi < n

Companies:
Adobe, Amazon

Related Topics:
Array, Backtracking, Bit Manipulation, Enumeration

Solution 1. Bitmask

The number of buildings is at most 20, and the number of requests is at most 16. This implies that we can consider using bitmask.

We want to find the largest combination of the requests that is valid. There are 2^16 = 65536 combinations at most.

For each combination, we need to traverse the edges in this combination, log the balance at each building, and check if all the buildings have zero balances. These takes O(M + N) time.

// OJ: https://leetcode.com/problems/maximum-number-of-achievable-transfer-requests/
// Author: github.com/lzl124631x
// Time: O(2^M * (M + N)) where M is the number of requests.
// Space: O(N)
class Solution {
public:
    int maximumRequests(int n, vector<vector<int>>& A) {
        int M = A.size(), ans = 0, cnt[20] = {};
        auto valid = [&](int m) {
            memset(cnt, 0, sizeof(cnt));
            for (int i = 0; i < M; ++i) {
                if ((m >> i & 1) == 0) continue;
                --cnt[A[i][0]];
                ++cnt[A[i][1]];
            }
            for (int i = 0; i < n; ++i) {
                if (cnt[i]) return false;
            }
            return true;
        };
        for (int m = 1; m < (1 << M); ++m) {
            if (valid(m)) ans = max(ans, __builtin_popcount(m));
        }
        return ans;
    }
};

Solution 2. DFS

Since we need to generate different combinations of M edges, we can use DFS to generate such combinations.

// OJ: https://leetcode.com/problems/maximum-number-of-achievable-transfer-requests/
// Author: github.com/lzl124631x
// Time: O(2^M * N)
// Space: O(N)
class Solution {
public:
    int maximumRequests(int n, vector<vector<int>>& A) {
        int cnt[20] = {}, ans = 0; // cnt[i] is available spots at building `i`
        function<void(int, int)> dfs = [&](int i, int used) {
            if (i == A.size()) {
                for (int j = 0; j < n; ++j) {
                    if (cnt[j]) return; // if any building has non-zero available spots, this combination is not valid, skip.
                }
                ans = max(ans, used); // otherwise, this combination is valid. 
                return;
            }
            int u = A[i][0], v = A[i][1];
            cnt[u]++, cnt[v]--; 
            dfs(i + 1, used + 1); // use this edge A[i]. Available spot at building u increments, and that of building v decrements.
            cnt[u]--, cnt[v]++;
            dfs(i + 1, used); // don't use this edge A[i]
        };
        dfs(0, 0); // dfs from A[0] with 0 used edges.
        return ans;
    }
};