1584

1584. Min Cost to Connect All Points (Medium)

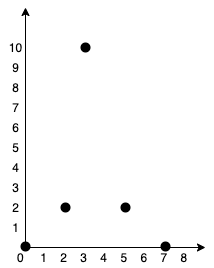
You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].

The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.

Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.

 

Example 1:

Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
Output: 20
Explanation: 

We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.

Example 2:

Input: points = [[3,12],[-2,5],[-4,1]]
Output: 18

 

Constraints:

• 1 <= points.length <= 1000
• -106 <= xi, yi <= 106
• All pairs (xi, yi) are distinct.

Companies: Microsoft, Amazon, Directi

Related Topics:
Array, Union Find, Graph, Minimum Spanning Tree

Similar Questions:

• Minimum Number of Lines to Cover Points (Medium)

Solution 1. Kruskal

The run time is too restrict. If you sort the edges then use Kruskal you will get TLE. The time complexity is O(N^2 * log(N^2)).

We have to use min heap instead so that the time complexity is O(K * log(N^2)) where K is the number of edges we need to scan to complete the tree. It's much smaller than N^2 on average.

// OJ: https://leetcode.com/problems/min-cost-to-connect-all-points/
// Author: github.com/lzl124631x
// Time: O(K * log(N^2)) where K is the number of edged we need to scan to complete the tree
// Space: O(N^2)
// Ref: https://leetcode.com/problems/min-cost-to-connect-all-points/discuss/843940/C%2B%2B-Minimum-Spanning-Tree-(Kruskal)
class UnionFind {
    vector<int> id;
    int size;
public:
    UnionFind(int N) : id(N), size(N) {
        iota(begin(id), end(id), 0);
    }
    int find(int a) {
        return id[a] == a ? a : (id[a] = find(id[a]));
    }
    void connect(int a, int b) {
        int p = find(a), q = find(b);
        if (p == q) return;
        id[p] = q;
        --size;
    }
    bool connected(int a, int b) {
        return find(a) == find(b);
    }
    int getSize() { return size; }
};
class Solution {
    typedef array<int, 3> Edge;
public:
    int minCostConnectPoints(vector<vector<int>>& A) {
        int N = A.size(), ans = 0;
        priority_queue<Edge, vector<Edge>, greater<Edge>> q;
        for (int i = 0; i < N; ++i) {
            for (int j = i + 1; j < N; ++j) q.push({ abs(A[i][0] - A[j][0]) + abs(A[i][1] - A[j][1]), i, j });
        }
        UnionFind uf(N);
        while (uf.getSize() > 1) {
            auto [w, u, v] = q.top();
            q.pop();
            if (uf.connected(u, v)) continue;
            uf.connect(u, v);
            ans += w;
        } 
        return ans;
    }
};

Solution 2. Prim

1. Start from a random node (we use 0 here), add it to the minimum spanning tree (MST).
2. From all the edges connecting nodes in the MST and those outside of the MST, find the edge with the mimimal cost, and add the corresponding node to the MST.
3. Repeat Step 2 until all the nodes are added into the MST.

// OJ: https://leetcode.com/problems/min-cost-to-connect-all-points/
// Author: github.com/lzl124631x
// Time: O(N^2)
// Space: O(N)
// Ref: https://leetcode.com/problems/min-cost-to-connect-all-points/discuss/843921/PythonGolang-Just-add-points-greedily
class Solution {
public:
    int minCostConnectPoints(vector<vector<int>>& A) {
        int N = A.size(), ans = 0, cur = 0;
        vector<int> dist(N, INT_MAX), seen(N);
        for (int i = 0; i < N - 1; ++i) {
            int x = A[cur][0], y = A[cur][1];
            seen[cur] = 1;
            for (int j = 0; j < N; ++j) {
                if (seen[j]) continue;
                dist[j] = min(dist[j], abs(A[j][0] - x) + abs(A[j][1] - y)); // use `cur` to relax the distance of all unconnected nodes
            }
            cur = min_element(begin(dist), end(dist)) - begin(dist); // greedily pick an unconnected node with the minimum distance
            ans += dist[cur];
            dist[cur] = INT_MAX; // mark this distance as used
        }
        return ans;
    }
};

Or the heap version. Note that the heap version is not more performant because all the nodes are interconnected in this graph. If the nodes are sparsely connected, the heap version is better.

// OJ: https://leetcode.com/problems/min-cost-to-connect-all-points
// Author: github.com/lzl124631x
// Time: O(N^2 * log(N^2))
// Space: O(N^2)
class Solution {
public:
    int minCostConnectPoints(vector<vector<int>>& A) {
        int N = A.size(), ans = 0;
        typedef pair<int, int> PII;
        priority_queue<PII, vector<PII>, greater<>> pq;
        vector<int> dist(N, INT_MAX), seen(N);
        dist[0] = 0;
        pq.emplace(0, 0);
        while (pq.size()) {
            auto [cost, i] = pq.top();
            pq.pop();
            if (seen[i]) continue;
            ans += dist[i];
            seen[i] = 1;
            for (int j = 0; j < N; ++j) {
                if (seen[j]) continue;
                int d = abs(A[j][0] - A[i][0]) + abs(A[j][1] - A[i][1]);
                if (d < dist[j]) {
                    dist[j] = d;
                    pq.emplace(d, j);
                }
            }
        }
        return ans;
    }
};