You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given an array relations where relations[i] = [prevCoursei, nextCoursei], representing a prerequisite relationship between course prevCoursei and course nextCoursei: course prevCoursei has to be taken before course nextCoursei. Also, you are given the integer k.
In one semester, you can take at most k courses as long as you have taken all the prerequisites in the previous semester for the courses you are taking.
Return the minimum number of semesters needed to take all courses. The testcases will be generated such that it is possible to take every course.
Example 1:
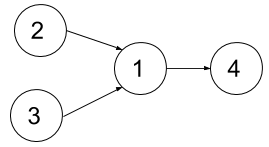
Input: n = 4, dependencies = [[2,1],[3,1],[1,4]], k = 2 Output: 3 Explanation: The figure above represents the given graph. In the first semester, you can take courses 2 and 3. In the second semester, you can take course 1. In the third semester, you can take course 4.
Example 2:
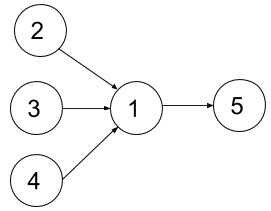
Input: n = 5, dependencies = [[2,1],[3,1],[4,1],[1,5]], k = 2 Output: 4 Explanation: The figure above represents the given graph. In the first semester, you can take courses 2 and 3 only since you cannot take more than two per semester. In the second semester, you can take course 4. In the third semester, you can take course 1. In the fourth semester, you can take course 5.
Example 3:
Input: n = 11, dependencies = [], k = 2 Output: 6
Constraints:
1 <= n <= 151 <= k <= n0 <= relations.length <= n * (n-1) / 2relations[i].length == 21 <= prevCoursei, nextCoursei <= nprevCoursei != nextCoursei- All the pairs
[prevCoursei, nextCoursei]are unique. - The given graph is a directed acyclic graph.
Related Topics:
Dynamic Programming, Bit Manipulation, Graph, Bitmask
Similar Questions:
Many people mentioned the solution which uses topological sort and greedily picking the classes with the most outdegrees. It is wrong considering the following example.
1 2 level 2
\ |
3 4 level 1
\ |
\ |
5 level 0
All classes have the same outdegree but we should take classes 1 and 2 first. The answer should be 3.
Then the 2nd idea is that we take the classes with the maximum level first.
But there is also counter example of this solution...
6
[[1,4],[2,4],[3,4],[3,5],[3,6]]
2
1 2 3
\ | / | \
4 5 6
The classes 1, 2, 3 are all at level 1, but we should take 3 first.
Then shall we sort on both level and outdegrees?
It's still wrong. Counter example below:
9
[[1,4],[1,5],[2,5],[2,6],[3,6],[3,7],[8,4],[8,5],[9,6],[9,7]]
3
Classes 1, 2, 3, 8, 9 have the same outdegree and level but we should pick 1, 2, 8 or 2, 3,9 first.
Anyway, these greedy ideas are incorrect.
Just for reference, I put the greedy solution using depth below.
// OJ: https://leetcode.com/problems/parallel-courses-ii/
// Author: github.com/lzl124631x
// Time: O((V + E) * logV)
// Space: O(V + E)
// NOTE: this is a wrong answer.
class Solution {
int dfs(vector<vector<int>> &G, vector<int> &level, int u) {
if (level[u] != -1) return level[u];
int d = 0;
for (int v : G[u]) d = max(d, dfs(G, level, v) + 1);
return level[u] = d;
}
public:
int minNumberOfSemesters(int N, vector<vector<int>>& E, int K) {
vector<vector<int>> G(N);
vector<int> indegree(N), level(N, -1);
for (auto &e : E) {
G[e[0] - 1].push_back(e[1] - 1);
indegree[e[1] - 1]++;
}
for (int i = 0; i < N; ++i) dfs(G, level, i);
auto cmp = [](vector<int> &a, vector<int> &b) { return a[1] < b[1]; };
priority_queue<vector<int>, vector<vector<int>>, decltype(cmp)> pq(cmp);
for (int i = 0; i < N; ++i) {
if (indegree[i] == 0) pq.push({ i, level[i] });
}
int ans = 0;
while (pq.size()) {
vector<vector<int>> next;
int cnt = 0;
while (pq.size() && cnt < K) {
int u = pq.top()[0];
pq.pop();
++cnt;
for (int v : G[u]) {
if (--indegree[v] == 0) next.push_back({ v, level[v] });
}
}
++ans;
for (auto &n : next) pq.push(n);
}
return ans;
}
};If the j-th bit of pre[i] is 1, then there is an edge from j to i.
Let dp[i] be the minimum number of semesters needed to take all the courses specified in i. If the j-th bit of i is 1, then j-th class is considered.
Trivial case: dp[0] = 0. It takes no semester to finish 0 courses.
Initialization: dp[i] = N because it won't take more than N semesters to finish all courses.
dp[i | s] = min( dp[i] + 1 | `s` is a non-empty subset of `next` and there are no more than K bits in `s`)
where `next` is the set of next available courses if courses in `i` are taken.
// OJ: https://leetcode.com/problems/parallel-courses-ii/
// Author: github.com/lzl124631x
// Time: O(3^N)
// Space: O(2^N)
class Solution {
public:
int minNumberOfSemesters(int N, vector<vector<int>>& E, int K) {
vector<int> pre(N), dp(1 << N, N);
for (auto &e : E) pre[e[1] - 1] |= 1 << (e[0] - 1);
dp[0] = 0;
for (int m = 0; m < (1 << N); ++m) {
int next = 0;
for (int i = 0; i < N; ++i) {
if ((m & pre[i]) == pre[i]) next |= 1 << i; // If the current course set `m` covers all the prerequisite classes of `i`-th class, we can take `i`-th class.
}
next &= ~m; // remove the classes that are already covered by `m`.
for (int s = next; s; s = (s - 1) & next) { // enumerate all the non-empty subset of `next`.
if (__builtin_popcount(s) <= K) dp[m | s] = min(dp[m | s], dp[m] + 1);
}
}
return dp.back();
}
};The code above uses push mode -- using the current dp value to update future dp values.
The code below uses pull mode -- using computed dp values to update the current dp value.
// OJ: https://leetcode.com/problems/parallel-courses-ii/
// Author: github.com/lzl124631x
// Time: O(3^N)
// Space: O(2^N)
class Solution {
public:
int minNumberOfSemesters(int n, vector<vector<int>>& E, int k) {
vector<int> prev(n), deps(1 << n), dp(1 << n, n);
dp[0] = 0;
for (auto &e : E) prev[e[1] - 1] |= 1 << (e[0] - 1);
for (int mask = 1; mask < (1 << n); ++mask) {
int lb = mask & -mask;
deps[mask] = deps[mask - lb] | prev[__builtin_ctz(lb)];
}
for (int mask = 1; mask < (1 << n); ++mask) {
for (int sub = mask; sub; sub = (sub - 1) & mask) {
if (__builtin_popcount(sub) > k) continue;
int pre = mask - sub, dep = deps[sub];
if ((pre & dep) != dep) continue;
dp[mask] = min(dp[mask], dp[pre] + 1);
}
}
return dp[(1 << n) - 1];
}
};