1478

1478. Allocate Mailboxes (Hard)

Given the array houses and an integer k. where houses[i] is the location of the ith house along a street, your task is to allocate k mailboxes in the street.

Return the minimum total distance between each house and its nearest mailbox.

The answer is guaranteed to fit in a 32-bit signed integer.

 

Example 1:

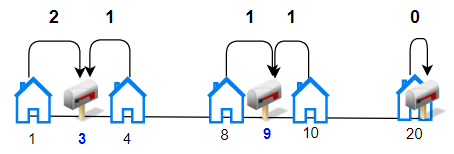
Input: houses = [1,4,8,10,20], k = 3
Output: 5
Explanation: Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5 

Example 2:

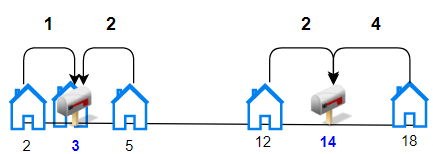
Input: houses = [2,3,5,12,18], k = 2
Output: 9
Explanation: Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.

Example 3:

Input: houses = [7,4,6,1], k = 1
Output: 8

Example 4:

Input: houses = [3,6,14,10], k = 4
Output: 0

 

Constraints:

• n == houses.length
• 1 <= n <= 100
• 1 <= houses[i] <= 10^4
• 1 <= k <= n
• Array houses contain unique integers.

Related Topics:
Math, Dynamic Programming

Solution 1. DP

Given i and j which are the indexes of two houses, what's the optimal mailbox position?

Consider input [1, 4, 10], we should put the mailbox at 4.

Consider input [1, 2, 4, 10], we should put the mailbox at a position in range [2, 4]. Assume we pick 2.

So in both cases we can pick A[(i + j) / 2].

Let dist(i, j) be this optimal total distance. dist(i, j) = sum( abs(A[k] - A[(i + j) / 2] | i <= k <= j ).

Let dp[k][i + 1] be the answer to the subproblem with k mailboxes and houses [0 .. i].

For dp[k][i + 1], we can try spliting with length j such that houses [0 .. j-1] use k - 1 mailboxes and houses [j .. i] use one mailbox.

dp[k][i + 1] = min( dp[k - 1][j] + dist[j][i] | k - 1 <= j <= i ) where k <= i + 1

dp[1][i + 1] = dist[0][i]

// OJ: https://leetcode.com/problems/allocate-mailboxes/
// Author: github.com/lzl124631x
// Time: O(N^3)
// Space: O(N^2)
class Solution {
public:
    int minDistance(vector<int>& A, int K) {
        if (A.size() == K) return 0;
        sort(begin(A), end(A));
        int N = A.size(); 
        vector<vector<int>> dist(N, vector<int>(N));
        for (int i = 0; i < N; ++i) {
            for (int j = 0; j < N; ++j) {
                int m = A[(i + j) / 2];
                for (int k = i; k <= j; ++k) dist[i][j] += abs(A[k] - m);
            }
        }
        vector<vector<int>> dp(K + 1, vector<int> (N + 1, 1e6));
        for (int i = 0; i < N; ++i) dp[1][i + 1] = dist[0][i];
        for (int k = 2; k <= K; ++k) {
            for (int i = 0; i < N; ++i) {
                for (int j = i; j >= k - 1; --j) {
                    dp[k][i + 1] = min(dp[k][i + 1], dp[k - 1][j] + dist[j][i]);
                }
            }
        }
        return dp[K][N];
    }
};

Solution 2. DP

Consider input [1, 4, 10], we should put the mailbox at 4 so that the total distance is 10 - 1.

Consider input [1, 2, 4, 10], we should put the mailbox at a position in range [2, 4], so that the total distance is (4 + 10) - (1 + 2).

Let dist(i, j) be this optimal total distance. dist(i, j) = sum((i + j + 1) / 2, j) - sum(i, (i + j) / 2), where sum(a, b) = sum( A[i] | a <= i <= b ).

Let presum[i + 1] = sum( A[k] | 0 <= k <= i ). Then sum(a, b) = presum(b + 1) - presum(a), so:

dist(i, j) = (presum(j + 1) - presum((i + j + 1) / 2)) - (presum((i + j) / 2 + 1) - presum(i))

Another optimization is that we can use 1D array for dp.

// OJ: https://leetcode.com/problems/allocate-mailboxes/
// Author: github.com/lzl124631x
// Time: O(N^2 * K)
// Space: O(N)
// Ref: https://leetcode.com/problems/allocate-mailboxes/discuss/685403/JavaC%2B%2BPython-DP-Solution
class Solution {
    int dist(vector<int> &presum, int i, int j) {
        return (presum[j + 1] - presum[(i + j + 1) / 2]) - (presum[(i + j) / 2 + 1] - presum[i]);
    }
public:
    int minDistance(vector<int>& A, int K) {
        if (A.size() == K) return 0;
        sort(begin(A), end(A));
        int N = A.size(); 
        vector<int> presum(N + 1);
        for (int i = 0; i < N; ++i) presum[i + 1] = presum[i] + A[i];
        vector<int> dp(N + 1, 1e6);
        for (int i = 0; i < N; ++i) dp[i + 1] = dist(presum, 0, i);
        for (int k = 2; k <= K; ++k) {
            for (int i = N - 1; i >= 0; --i) {
                for (int j = i; j >= k - 1; --j) {
                    dp[i + 1] = min(dp[i + 1], dp[j] + dist(presum, j, i));
                }
            }
        }
        return dp[N];
    }
};