Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.
Return the number of pseudo-palindromic paths going from the root node to leaf nodes.
Example 1:
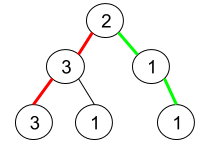
Input: root = [2,3,1,3,1,null,1] Output: 2 Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).
Example 2:
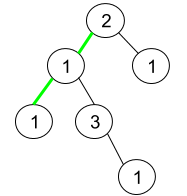
Input: root = [2,1,1,1,3,null,null,null,null,null,1] Output: 1 Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).
Example 3:
Input: root = [9] Output: 1
Constraints:
- The given binary tree will have between
1and10^5nodes. - Node values are digits from
1to9.
Related Topics:
Bit Manipulation, Tree, Depth-first Search
A path is pseudo-palindromic if there is at most 1 digit with odd occurrences in the path.
We can use pre-order traversal and keep track of the count of occurrences of digits in cnt array.
If we meet a leaf node and there is at most 1 digit with odd occurrences, we increment the answer.
// OJ: https://leetcode.com/problems/pseudo-palindromic-paths-in-a-binary-tree/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(H)
class Solution {
int cnt[10] = {}, ans = 0;
void dfs(TreeNode *root) {
if (!root) return;
cnt[root->val]++;
if (!root->left && !root->right) {
int c = 0;
for (int i = 1; i < 10; ++i) {
c += cnt[i] % 2;
if (c >= 2) break;
}
if (c < 2) ++ans;
}
dfs(root->left);
dfs(root->right);
cnt[root->val]--;
}
public:
int pseudoPalindromicPaths (TreeNode* root) {
dfs(root);
return ans;
}
};Another variation that doesn't require the O(9) check of the count of odd occurrences.
// OJ: https://leetcode.com/problems/pseudo-palindromic-paths-in-a-binary-tree/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(H)
class Solution {
int cnt[10] = {}, odd = 0, ans = 0;
void dfs(TreeNode *root) {
if (!root) return;
cnt[root->val]++;
int diff = cnt[root->val] % 2 ? 1 : -1;
odd += diff;
ans += !root->left && !root->right && odd < 2;
dfs(root->left);
dfs(root->right);
odd -= diff;
cnt[root->val]--;
}
public:
int pseudoPalindromicPaths (TreeNode* root) {
dfs(root);
return ans;
}
};