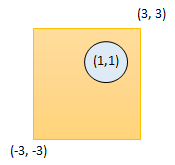1401

1401. Circle and Rectangle Overlapping (Medium)

Given a circle represented as (radius, x_center, y_center) and an axis-aligned rectangle represented as (x1, y1, x2, y2), where (x1, y1) are the coordinates of the bottom-left corner, and (x2, y2) are the coordinates of the top-right corner of the rectangle.

Return True if the circle and rectangle are overlapped otherwise return False.

In other words, check if there are any point (xi, yi) such that belongs to the circle and the rectangle at the same time.

 

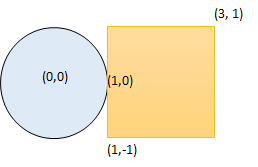
Example 1:

Input: radius = 1, x_center = 0, y_center = 0, x1 = 1, y1 = -1, x2 = 3, y2 = 1
Output: true
Explanation: Circle and rectangle share the point (1,0) 

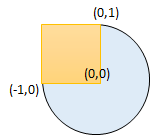
Example 2:

Input: radius = 1, x_center = 0, y_center = 0, x1 = -1, y1 = 0, x2 = 0, y2 = 1
Output: true

Example 3:

Input: radius = 1, x_center = 1, y_center = 1, x1 = -3, y1 = -3, x2 = 3, y2 = 3
Output: true

Example 4:

Input: radius = 1, x_center = 1, y_center = 1, x1 = 1, y1 = -3, x2 = 2, y2 = -1
Output: false

 

Constraints:

• 1 <= radius <= 2000
• -10^4 <= x_center, y_center, x1, y1, x2, y2 <= 10^4
• x1 < x2
• y1 < y2

Related Topics:
Geometry

Solution 1.

Move the center of the circle to the coordinate origin (0, 0), then this problem becomes "is there a point (x, y) (x1 <= x <= x2, y1 <= y <= y2) satisfying x^2 + y^2 <= r^2".

So just compute minimum values of x^2 and y^2, then compare the sum with r^2..

// OJ: https://leetcode.com/problems/circle-and-rectangle-overlapping/
// Author: github.com/lzl124631x
// Time: O(1)
// Space: O(1)
class Solution {
public:
    bool checkOverlap(int radius, int x_center, int y_center, int x1, int y1, int x2, int y2) {
        x1 -= x_center; x2 -= x_center;
        y1 -= y_center; y2 -= y_center;
        int minX = x1 * x2 > 0 ? min(x1*x1, x2*x2) : 0, minY = y1 * y2 > 0 ? min(y1*y1, y2*y2) : 0;
        return minY + minX <= radius * radius;
    }
};