1388

1388. Pizza With 3n Slices (Hard)

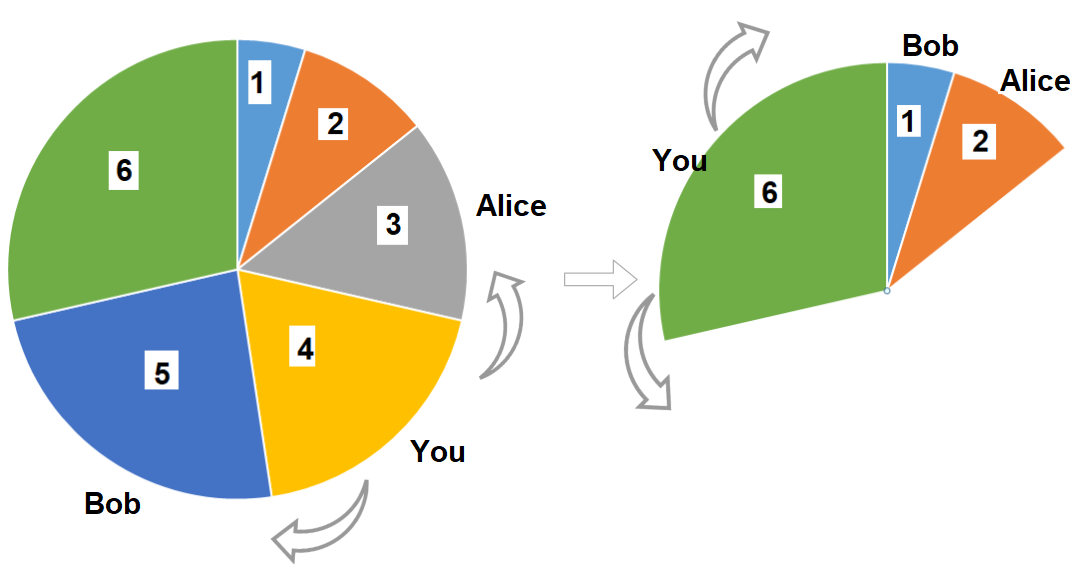
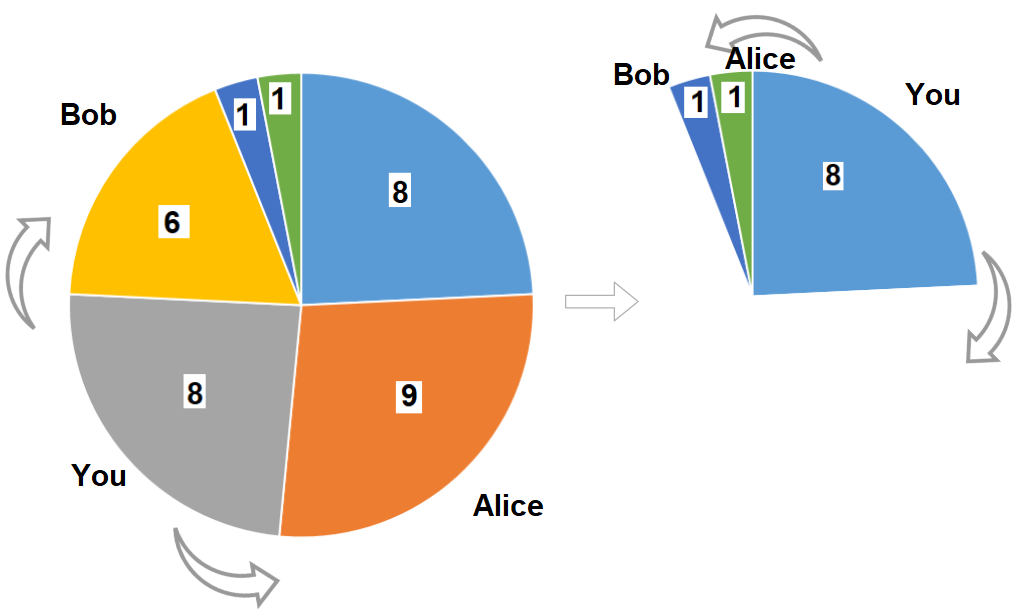
There is a pizza with 3n slices of varying size, you and your friends will take slices of pizza as follows:

• You will pick any pizza slice.
• Your friend Alice will pick next slice in anti clockwise direction of your pick. 
• Your friend Bob will pick next slice in clockwise direction of your pick.
• Repeat until there are no more slices of pizzas.

Sizes of Pizza slices is represented by circular array slices in clockwise direction.

Return the maximum possible sum of slice sizes which you can have.

 

Example 1:

Input: slices = [1,2,3,4,5,6]
Output: 10
Explanation: Pick pizza slice of size 4, Alice and Bob will pick slices with size 3 and 5 respectively. Then Pick slices with size 6, finally Alice and Bob will pick slice of size 2 and 1 respectively. Total = 4 + 6.

Example 2:

Input: slices = [8,9,8,6,1,1]
Output: 16
Output: Pick pizza slice of size 8 in each turn. If you pick slice with size 9 your partners will pick slices of size 8.

Example 3:

Input: slices = [4,1,2,5,8,3,1,9,7]
Output: 21

Example 4:

Input: slices = [3,1,2]
Output: 3

 

Constraints:

• 1 <= slices.length <= 500
• slices.length % 3 == 0
• 1 <= slices[i] <= 1000

Related Topics:
Dynamic Programming

Solution 1. DP

This problem is equivalent to "Given an integer array with size 3N, select N integers with maximum sum and any selected integers are not next to each other in the array."

To solve the circlar array problem, we can do a same trick as in 213. House Robber II (Medium) -- apply DP to A[0..(N-2)] and A[1..(N-1)] (which means we fork between picking the first element and not picking the first element).

Now let's consider the subproblem for A[0..(N-2)] and A[1..(N-1)].

Assume the input array is B whose length is M=N-1.

Let dp[i + 1][j] be the maximum sum of size you can get at ith pizza with j pieces left for you to pick.

If we don't pick A[i], dp[i + 1][j] = dp[i][j]. Otherwise, dp[i + 1][j] = B[i] + dp[i-1][j-1].

So we have:

dp[i + 1][j] = max(dp[i][j], B[i] + dp[i-1][j-1]) where 0 <= i < M and 1 <= j <= N/3

Now consider special cases.

1. dp[i+1][0] = 0.
2. dp[i+1][j] = -INF where j > i / 2 + 1 because for i + 1 elements, we at most pick i / 2 + 1 elements.
3. When i == 0, the above formula becomes dp[1][j] = max(dp[0][j], B[0] + dp[-1][j-1]) which should be dp[1][j] = B[0]. So we can regard dp[-1][j] = 0.

// OJ: https://leetcode.com/problems/pizza-with-3n-slices/
// Author: github.com/lzl124631x
// Time: O(N^2)
// Space: O(N^2)
class Solution {
    int solve(vector<int> A, int cnt) {
        int N = A.size();
        vector<vector<int>> dp(N + 1, vector<int>(cnt + 1, -1e9));
        for (int i = 0; i <= N; ++i) dp[i][0] = 0;
        for (int i = 0; i < N; ++i) {
            for (int j = 1; j <= min(cnt, i / 2 + 1); ++j) {
                dp[i + 1][j] = max(dp[i][j], (i == 0 ? 0 : dp[i - 1][j - 1]) + A[i]);
            }
        }
        return dp[N][cnt];
    }
public:
    int maxSizeSlices(vector<int>& A) {
        int N = A.size(), ans = 0;
        return max(solve(vector<int>(A.begin(), A.end() - 1), N / 3),
                    solve(vector<int>(A.begin() + 1, A.end()), N / 3));
    }
};

Solution 2. DP + Space Optimization

Since dp[i + 1][j] is only dependent on dp[i][j] and dp[i - 1][j - 1], we can reduce the dp array from N * (N / 3) to 3 * (N / 3).

// OJ: https://leetcode.com/problems/pizza-with-3n-slices/
// Author: github.com/lzl124631x
// Time: O(N^2)
// Space: O(N)
class Solution {
    int solve(vector<int> A, int cnt) {
        int N = A.size();
        vector<vector<int>> dp(3, vector<int>(cnt + 1, -1e9));
        for (int i = 0; i < 3; ++i) dp[i][0] = 0;
        for (int i = 0; i < N; ++i) {
            for (int j = 1; j <= min(cnt, i / 2 + 1); ++j) {
                dp[(i + 1) % 3][j] = max(dp[i % 3][j], (i == 0 ? 0 : dp[(i + 2) % 3][j - 1]) + A[i]);
            }
        }
        return dp[N % 3][cnt];
    }
public:
    int maxSizeSlices(vector<int>& A) {
        int N = A.size(), ans = 0;
        return max(solve(vector<int>(A.begin(), A.end() - 1), N / 3),
                    solve(vector<int>(A.begin() + 1, A.end()), N / 3));
    }
};

Solution 3. DP + Space Optimization

If we swap i and j, then dp[i][j + 1] is dependent on dp[i][j] and dp[i - 1][j - 1], we can reduce the dp array further to 2 * N.

// OJ: https://leetcode.com/problems/pizza-with-3n-slices/
// Author: github.com/lzl124631x
// Time: O(N^2)
// Space: O(N)
class Solution {
    int solve(vector<int> A, int cnt) {
        int N = A.size();
        vector<vector<int>> dp(2, vector<int>(N + 1, -1e9));
        for (int i = 0; i < N + 1; ++i) dp[0][i] = 0;
        for (int i = 1; i <= cnt; ++i) {
            for (int j = 0; j < N; ++j) {
                if (i > j / 2 + 1) dp[i % 2][j + 1] = -1e9;
                else dp[i % 2][j + 1] = max(dp[i % 2][j], (j == 0 ? 0 : dp[(i - 1) % 2][j - 1]) + A[j]);
            }
        }
        return dp[cnt % 2][N];
    }
public:
    int maxSizeSlices(vector<int>& A) {
        int N = A.size(), ans = 0;
        return max(solve(vector<int>(A.begin(), A.end() - 1), N / 3),
                    solve(vector<int>(A.begin() + 1, A.end()), N / 3));
    }
};

Solution 4. DP + Space Optimization

If we use temp variables to store dp[i - 1][j - 1], we can further reduce the space complexity to 1 * N.

// OJ: https://leetcode.com/problems/pizza-with-3n-slices/
// Author: github.com/lzl124631x
// Time: O(N^2)
// Space: O(N)
class Solution {
    int solve(vector<int> A, int cnt) {
        int N = A.size();
        vector<int> dp(N + 1);
        for (int i = 1; i <= cnt; ++i) {
            int prev, prev2 = 0;
            for (int j = 0; j < N; ++j) {
                int cur = dp[j + 1];
                if (i > j / 2 + 1) dp[j + 1] = -1e9;
                else dp[j + 1] = max(dp[j], prev2 + A[j]);
                prev2 = prev;
                prev = cur;
            }
        }
        return dp[N];
    }
public:
    int maxSizeSlices(vector<int>& A) {
        int N = A.size(), ans = 0;
        return max(solve(vector<int>(A.begin(), A.end() - 1), N / 3),
                    solve(vector<int>(A.begin() + 1, A.end()), N / 3));
    }
};