Given a binary tree root, the task is to return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).
Assume a BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.
Example 1:
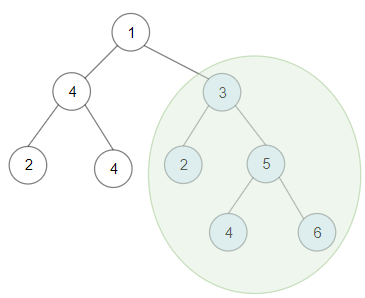
Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6] Output: 20 Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.
Example 2:
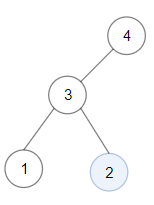
Input: root = [4,3,null,1,2] Output: 2 Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.
Example 3:
Input: root = [-4,-2,-5] Output: 0 Explanation: All values are negatives. Return an empty BST.
Example 4:
Input: root = [2,1,3] Output: 6
Example 5:
Input: root = [5,4,8,3,null,6,3] Output: 7
Constraints:
- Each tree has at most
40000nodes.. - Each node's value is between
[-4 * 10^4 , 4 * 10^4].
Related Topics:
Dynamic Programming, Binary Search Tree
// OJ: https://leetcode.com/problems/maximum-sum-bst-in-binary-tree/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(H)
class Solution {
int ans = 0;
pair<int, int> postorder(TreeNode *root) {
pair<int, int> r{root->val, root->val};
bool isBST = true;
if (root->left) {
auto left = postorder(root->left);
if (root->val <= left.second) isBST = false;
r.second = max(left.second, root->val);
r.first = min(left.first, root->val);
}
if (root->right) {
auto right = postorder(root->right);
if (root->val >= right.first) isBST = false;
r.second = max(right.second, root->val);
r.first = min(right.first, root->val);
}
root->val += (root->left ? root->left->val : 0) + (root->right ? root->right->val : 0);
if (isBST) ans = max(ans, root->val);
return isBST ? r : pair<int,int>{ INT_MIN, INT_MAX };
}
public:
int maxSumBST(TreeNode* root) {
if (!root) return 0;
postorder(root);
return ans;
}
};