1349

1349. Maximum Students Taking Exam (Hard)

Given a m * n matrix seats  that represent seats distributions in a classroom. If a seat is broken, it is denoted by '#' character otherwise it is denoted by a '.' character.

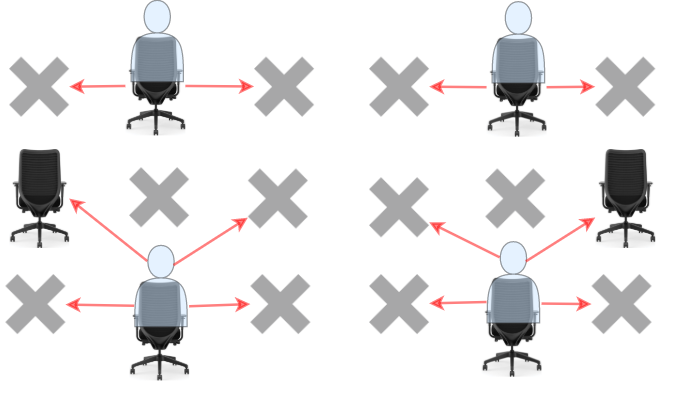
Students can see the answers of those sitting next to the left, right, upper left and upper right, but he cannot see the answers of the student sitting directly in front or behind him. Return the maximum number of students that can take the exam together without any cheating being possible..

Students must be placed in seats in good condition.

 

Example 1:

Input: seats = [["#",".","#","#",".","#"],
                [".","#","#","#","#","."],
                ["#",".","#","#",".","#"]]
Output: 4
Explanation: Teacher can place 4 students in available seats so they don't cheat on the exam. 

Example 2:

Input: seats = [[".","#"],
                ["#","#"],
                ["#","."],
                ["#","#"],
                [".","#"]]
Output: 3
Explanation: Place all students in available seats. 

Example 3:

Input: seats = [["#",".",".",".","#"],
                [".","#",".","#","."],
                [".",".","#",".","."],
                [".","#",".","#","."],
                ["#",".",".",".","#"]]
Output: 10
Explanation: Place students in available seats in column 1, 3 and 5.

 

Constraints:

• seats contains only characters '.' and'#'.
• m == seats.length
• n == seats[i].length
• 1 <= m <= 8
• 1 <= n <= 8

Related Topics:
Dynamic Programming

Solution 1. DP

// OJ: https://leetcode.com/problems/maximum-students-taking-exam/
// Author: github.com/lzl124631x
// Time: O(M * (2^N)^2)
// Space: O(M * 2^N)
// Ref: https://leetcode.com/problems/maximum-students-taking-exam/discuss/503686/A-simple-tutorial-on-this-bitmasking-problem
class Solution {
public:
    int maxStudents(vector<vector<char>>& A) {
        int M = A.size(), N = A[0].size();
        vector<int> states;
        for (int i = 0; i < M; ++i) {
            int cur = 0;
            for (int j = 0; j < N; ++j) cur = cur * 2 + (A[i][j] == '.');
            states.push_back(cur);
        }
        vector<vector<int>> dp(M + 1, vector<int>(1 << N, -1));
        dp[0][0] = 0;
        for (int i = 1; i <= M; ++i) {
            int state = states[i - 1];
            for (int j = 0; j < (1 << N); ++j) {
                if ((j & state) != j || (j & (j >> 1))) continue;
                int cnt = __builtin_popcount(j);
                for (int k = 0; k < (1 << N); ++k) {
                    if ((j & (k >> 1)) || (j & (k << 1)) || dp[i - 1][k] == -1) continue;
                    dp[i][j] = max(dp[i][j], dp[i - 1][k] + cnt);
                }
            }
        }
        return *max_element(begin(dp[M]), end(dp[M]));
    }
};