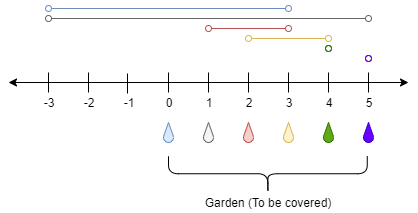
There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e The length of the garden is n).
There are n + 1 taps located at points [0, 1, ..., n] in the garden.
Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.
Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.
Example 1:
Input: n = 5, ranges = [3,4,1,1,0,0] Output: 1 Explanation: The tap at point 0 can cover the interval [-3,3] The tap at point 1 can cover the interval [-3,5] The tap at point 2 can cover the interval [1,3] The tap at point 3 can cover the interval [2,4] The tap at point 4 can cover the interval [4,4] The tap at point 5 can cover the interval [5,5] Opening Only the second tap will water the whole garden [0,5]
Example 2:
Input: n = 3, ranges = [0,0,0,0] Output: -1 Explanation: Even if you activate all the four taps you cannot water the whole garden.
Example 3:
Input: n = 7, ranges = [1,2,1,0,2,1,0,1] Output: 3
Example 4:
Input: n = 8, ranges = [4,0,0,0,0,0,0,0,4] Output: 2
Example 5:
Input: n = 8, ranges = [4,0,0,0,4,0,0,0,4] Output: 1
Constraints:
1 <= n <= 10^4ranges.length == n + 10 <= ranges[i] <= 100
Related Topics:
Dynamic Programming, Greedy
// OJ: https://leetcode.com/problems/minimum-number-of-taps-to-open-to-water-a-garden/
// Author: github.com/lzl124631x
// Time: O(NlogN)
// Space: O(N)
class Solution {
public:
int minTaps(int n, vector<int>& ranges) {
vector<pair<int, int>> v;
for (int i = 0; i < ranges.size(); ++i)
v.emplace_back(max(0, i - ranges[i]), min(n, i + ranges[i]));
sort(v.begin(), v.end());
int end = 0, newEnd = 0, ans = 0;
for (int i = 0; i < v.size() && end != n; ++i) {
if (v[i].first > end) return -1;
newEnd = max(newEnd, v[i].second);
if (i + 1 == v.size() || v[i + 1].first > end) {
end = newEnd;
++ans;
}
}
return ans;
}
};