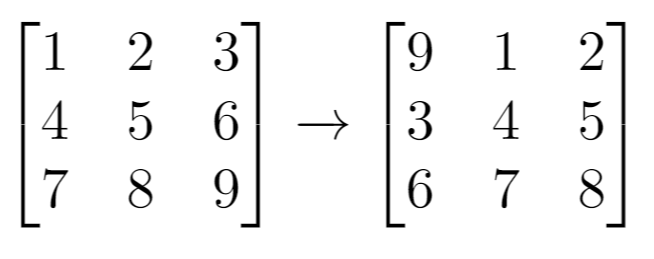1260

1260. Shift 2D Grid (Easy)

Given a 2D grid of size m x n and an integer k. You need to shift the grid k times.

In one shift operation:

• Element at grid[i][j] moves to grid[i][j + 1].
• Element at grid[i][n - 1] moves to grid[i + 1][0].
• Element at grid[m - 1][n - 1] moves to grid[0][0].

Return the 2D grid after applying shift operation k times.

 

Example 1:

Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
Output: [[9,1,2],[3,4,5],[6,7,8]]

Example 2:

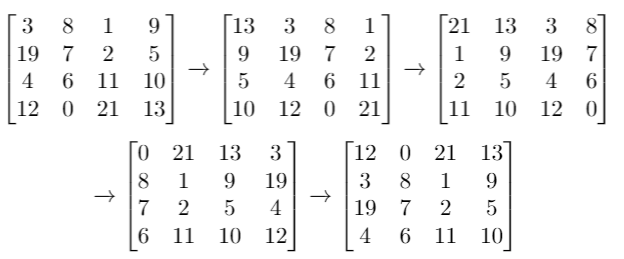
Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

Example 3:

Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
Output: [[1,2,3],[4,5,6],[7,8,9]]

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m <= 50
• 1 <= n <= 50
• -1000 <= grid[i][j] <= 1000
• 0 <= k <= 100

Companies:
Amazon

Related Topics:
Array, Matrix, Simulation

Solution 1.

// OJ: https://leetcode.com/problems/shift-2d-grid/
// Author: github.com/lzl124631x
// Time: O(MN)
// Space: O(K)
class Solution {
public:
    vector<vector<int>> shiftGrid(vector<vector<int>>& A, int k) {
        int M = A.size(), N = A[0].size();
        k %= M * N;
        if (k == 0) return A;
        queue<int> q;
        for (int i = 0; i < M * N + k; ++i) {
            int j = i % (M * N), x = j / N, y = j % N;
            if (i < k) q.push(A[x][y]);
            else {
                q.push(A[x][y]);
                A[x][y] = q.front();
                q.pop();
            }
        }
        return A;
    }
};

Solution 2. In-place Rotation

// OJ: https://leetcode.com/problems/shift-2d-grid/
// Author: github.com/lzl124631x
// Time: O(MN)
// Space: O(1)
class Solution {
public:
    vector<vector<int>> shiftGrid(vector<vector<int>>& A, int k) {
        int M = A.size(), N = A[0].size(), len = M * N;
        k %= len;
        if (k == 0) return A;
        for (int i = 0, cnt = 0; cnt < len; ++i) {
            int j = i, tmp = A[j / N][j % N]; 
            do {
                int next = (j + k) % len, nextVal = A[next / N][next % N];
                A[next / N][next % N] = tmp;
                tmp = nextVal;
                j = next;
                ++cnt;
            } while (j != i);
        }
        return A;
    }
};