1240

1240. Tiling a Rectangle with the Fewest Squares (Hard)

Given a rectangle of size n x m, return the minimum number of integer-sided squares that tile the rectangle.

 

Example 1:

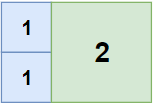
Input: n = 2, m = 3
Output: 3
Explanation: 3 squares are necessary to cover the rectangle.
2 (squares of 1x1)
1 (square of 2x2)

Example 2:

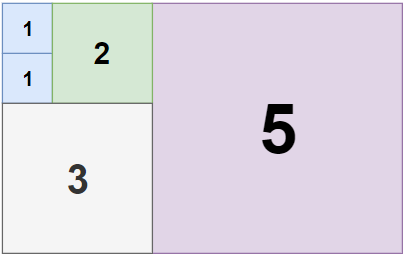
Input: n = 5, m = 8
Output: 5

Example 3:

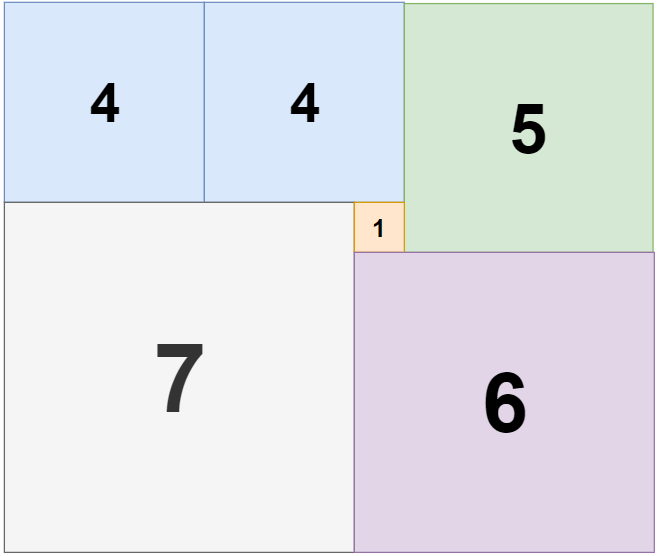
Input: n = 11, m = 13
Output: 6

 

Constraints:

• 1 <= n, m <= 13

Companies:
Google

Related Topics:
Dynamic Programming, Backtracking

Solution 1.

// OJ: https://leetcode.com/problems/tiling-a-rectangle-with-the-fewest-squares
// Author: github.com/lzl124631x
// Time: O()
// Space: O()
class Solution {
public:
    int tilingRectangle(int n, int m) {
        int ans = INT_MAX;
        vector<vector<bool>> A(n, vector<bool>(m));
        function<void(int)> dfs = [&](int cnt) {
            if (cnt >= ans) return;
            for (int i = 0; i < n; ++i) {
                for (int j = 0; j < m; ++j) {
                    if (!A[i][j]) {
                        int len = 1;
                        for (; i + len <= n && j + len <= m && cnt + 1 < ans; ++len) {
                            int x = 0, y = 0;
                            for (; y < len && !A[i + len - 1][j + y]; ++y);
                            if (y < len) break;
                            for (; x < len && !A[i + x][j + len - 1]; ++x);
                            if (x < len) break;
                            for (int y = 0; y < len; ++y) A[i + len - 1][j + y] = true;
                            for (int x = 0; x < len; ++x) A[i + x][j + len - 1] = true;
                            dfs(cnt + 1);
                        }
                        for (int x = 0; x < len - 1; ++x) {
                            for (int y = 0; y < len - 1; ++y) {
                                A[i + x][j + y] = false;
                            }
                        }
                        return;
                    }
                }
            }
            ans = min(ans, cnt);
        };
        dfs(0);
        return ans;
    }
};