In an infinite chess board with coordinates from -infinity to +infinity, you have a knight at square [0, 0].
A knight has 8 possible moves it can make, as illustrated below. Each move is two squares in a cardinal direction, then one square in an orthogonal direction.
Return the minimum number of steps needed to move the knight to the square [x, y]. It is guaranteed the answer exists.
Example 1:
Input: x = 2, y = 1 Output: 1 Explanation: [0, 0] → [2, 1]
Example 2:
Input: x = 5, y = 5 Output: 4 Explanation: [0, 0] → [2, 1] → [4, 2] → [3, 4] → [5, 5]
Constraints:
-300 <= x, y <= 3000 <= |x| + |y| <= 300
Companies: Citadel, Amazon, Expedia, Google, Indeed, Facebook, Booking.com, Microsoft, LinkedIn, Adobe, IMC, athenahealth, Nvidia
Related Topics:
Breadth-First Search
Similar Questions:
Hints:
- You can simulate the movements since the limits are low.
- Is there a search algorithm applicable to this problem?
- Since we want the minimum number of moves, we can use Breadth First Search.
Firstly, it's symmetric for axes. So let x = abs(x), y = abs(y).
Secondly, attempts with x or y values smaller than -1 should be ignored.
For example, to reach (1,1) from (0,0), the best way is to get (2,-1) or (-1,2) first, then (1,1) (two steps). If we eliminate all coordinates with negative numbers, then we can't reach (1,1) from (0,0) within two steps.
// OJ: https://leetcode.com/problems/minimum-knight-moves
// Author: github.com/lzl124631x
// Time: O(XY)
// Space: O(XY)
class Solution {
public:
int minKnightMoves(int x, int y) {
x = abs(x);
y = abs(y);
bool seen[302][302] = {};
seen[x + 1][y + 1] = true; // Since -1 is the only negative value, we offset the positions by 1. So (0,0) becomes (1,1) and (x,y) becomes (x+1,y+1)
queue<pair<int, int>> q{{{x + 1, y + 1}}};
int step = 0, dirs[8][2] = {{1,2},{2,1},{-1,2},{2,-1},{1,-2},{-2,1},{-1,-2},{-2,-1}};
while (q.size()) {
int cnt = q.size();
while (cnt--) {
auto [x, y] = q.front();
q.pop();
if (x == 1 && y == 1) return step;
for (auto &[dx, dy] : dirs) {
int a = x + dx, b = y + dy;
if (a < 0 || a > 301 || b < 0 || b > 301 || seen[a][b]) continue;
seen[a][b] = true;
q.emplace(a, b);
}
}
++step;
}
return -1;
}
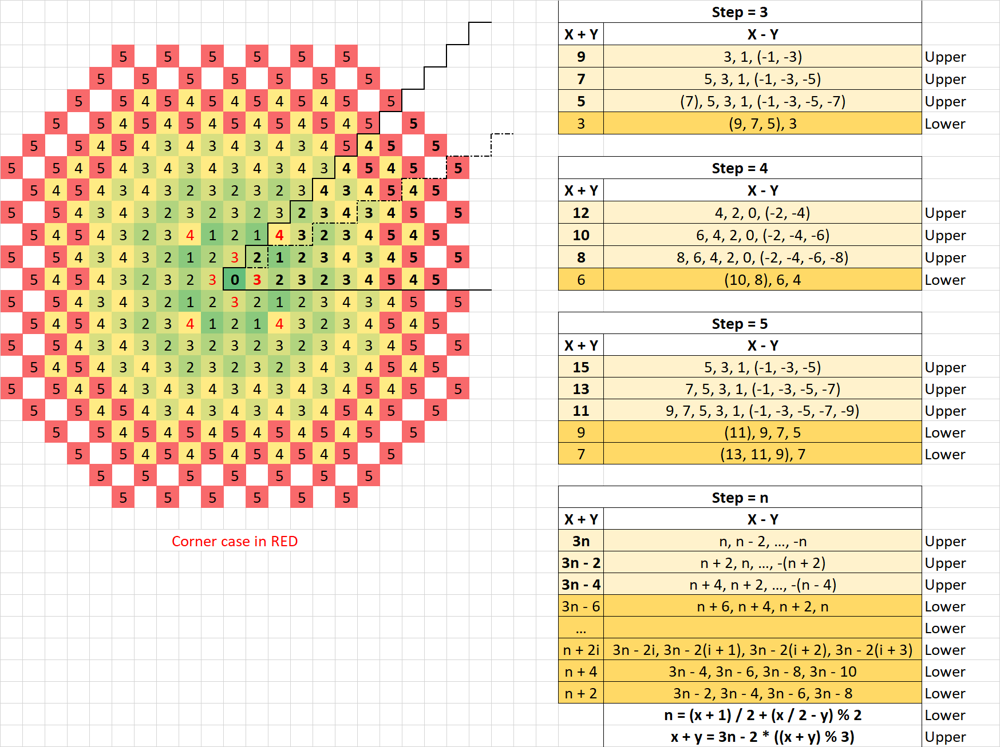
};Please stare at the image first:
Some interesting pattern here:
- Convert the
(x, y)intox >= y >= 0due to the 3 direction symmetry of the plot (now we reduce the plane to 1/8). - Then keep divide the problem into two parts: lower and upper.
- For lower half:
Noticexvalue is dominant the result.
(x + 1) / 2is the base indicate the steps generally grow 1 when x increase 2.
(x / 2 - y) % 2basically tunning the detail, because the number is meshed. - For upper half:
Noticex + yis dominant the result.
Also, ifstep = n, thenx + y = 3n or 3n - 2 or 3n - 4, always these 3 numbers.
Sonis a function ofx + y, why there is a exact match? becuase the reminder of3n,3n - 2,3n - 4cover all the mod of 3, which is0, 1, 2.
(x + y) % 3 == 0 -> x + y = 3n
(x + y) % 3 == 1 -> x + y = 3n - 2
(x + y) % 3 == 2 -> x + y = 3n - 4 = 3n - 2 * ((x + y) % 3)
n = (x + y + 2 * ((x + y) % 3)) / 3 = (x + y) / 3 + (x + y) % 3
// OJ: https://leetcode.com/problems/minimum-knight-moves/
// Author: github.com/lzl124631x
// Time: O(1)
// Space: O(1)
// Ref: https://leetcode.com/problems/minimum-knight-moves/discuss/682850/C%2B%2B-O(1)-Formula-solution-with-plot-explanation
class Solution {
public:
int minKnightMoves(int x, int y) {
x = abs(x);
y = abs(y);
if (x < y) swap(x, y);
if (x == 1 and y == 0) return 3;
if (x == 2 and y == 2) return 4;
if (y <= x / 2) {
return (x + 1) / 2 + (x / 2 - y) % 2;
}
return (x + y) / 3 + (x + y) % 3;
}
};