Skip to content

Latest commit

 

History

History
373 lines (289 loc) · 11.1 KB

0213.打家劫舍II.md

File metadata and controls

373 lines (289 loc) · 11.1 KB
Raw

参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

213.打家劫舍II

力扣题目链接

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，能够偷窃到的最高金额。

示例 1：

  • 输入：nums = [2,3,2]

  • 输出：3

  • 解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

  • 示例 2：

  • 输入：nums = [1,2,3,1]

  • 输出：4

  • 解释：你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。偷窃到的最高金额 = 1 + 3 = 4 。

  • 示例 3：

  • 输入：nums = [0]

  • 输出：0

提示：

  • 1 <= nums.length <= 100
  • 0 <= nums[i] <= 1000

算法公开课

《代码随想录》算法视频公开课：动态规划，房间连成环了那还偷不偷呢？| LeetCode：213.打家劫舍II，相信结合视频再看本篇题解，更有助于大家对本题的理解。

思路

这道题目和198.打家劫舍是差不多的，唯一区别就是成环了。

对于一个数组，成环的话主要有如下三种情况：

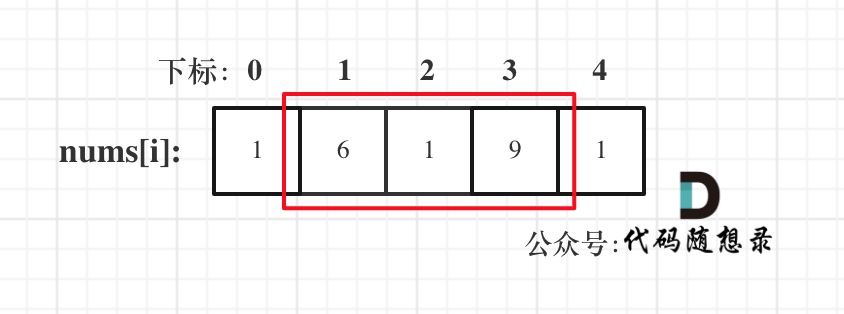
  • 情况一：考虑不包含首尾元素

213.打家劫舍II

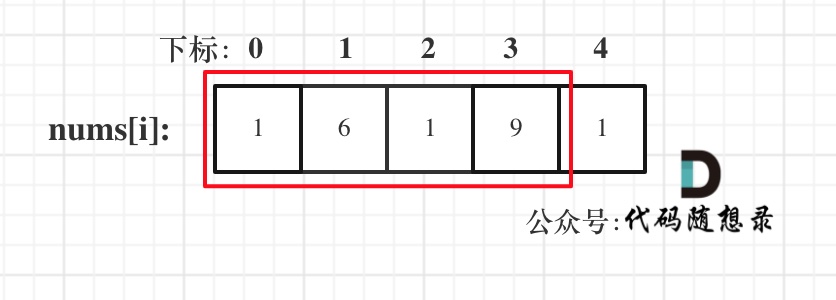
  • 情况二：考虑包含首元素，不包含尾元素

213.打家劫舍II1

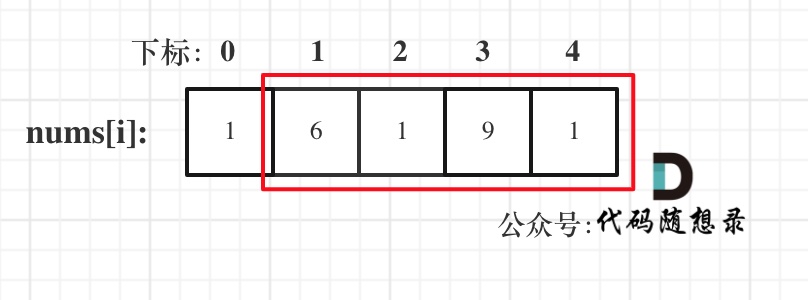
  • 情况三：考虑包含尾元素，不包含首元素

213.打家劫舍II2

注意我这里用的是"考虑"，例如情况三，虽然是考虑包含尾元素，但不一定要选尾部元素！ 对于情况三，取nums[1] 和 nums[3]就是最大的。

而情况二 和 情况三 都包含了情况一了，所以只考虑情况二和情况三就可以了。

分析到这里，本题其实比较简单了。 剩下的和198.打家劫舍就是一样的了。

代码如下：

// 注意注释中的情况二情况三，以及把198.打家劫舍的代码抽离出来了
class Solution {
public:
    int rob(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        if (nums.size() == 1) return nums[0];
        int result1 = robRange(nums, 0, nums.size() - 2); // 情况二
        int result2 = robRange(nums, 1, nums.size() - 1); // 情况三
        return max(result1, result2);
    }
    // 198.打家劫舍的逻辑
    int robRange(vector<int>& nums, int start, int end) {
        if (end == start) return nums[start];
        vector<int> dp(nums.size());
        dp[start] = nums[start];
        dp[start + 1] = max(nums[start], nums[start + 1]);
        for (int i = start + 2; i <= end; i++) {
            dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
        }
        return dp[end];
    }
};
  • 时间复杂度: O(n)
  • 空间复杂度: O(n)

总结

成环之后还是难了一些的， 不少题解没有把“考虑房间”和“偷房间”说清楚。

这就导致大家会有这样的困惑：情况三怎么就包含了情况一了呢？ 本文图中最后一间房不能偷啊，偷了一定不是最优结果。

所以我在本文重点强调了情况一二三是“考虑”的范围，而具体房间偷与不偷交给递推公式去抉择。

这样大家就不难理解情况二和情况三包含了情况一了。

其他语言版本

Java：

class Solution {
    public int rob(int[] nums) {
        if (nums == null || nums.length == 0)
            return 0;
        int len = nums.length;
        if (len == 1)
            return nums[0];
        return Math.max(robAction(nums, 0, len - 1), robAction(nums, 1, len));
    }

    int robAction(int[] nums, int start, int end) {
        int x = 0, y = 0, z = 0;
        for (int i = start; i < end; i++) {
            y = z;
            z = Math.max(y, x + nums[i]);
            x = y;
        }
        return z;
    }
}

Python：

class Solution:
    def rob(self, nums: List[int]) -> int:
        if len(nums) == 0:
            return 0
        if len(nums) == 1:
            return nums[0]
        
        result1 = self.robRange(nums, 0, len(nums) - 2)  # 情况二
        result2 = self.robRange(nums, 1, len(nums) - 1)  # 情况三
        return max(result1, result2)
    # 198.打家劫舍的逻辑
    def robRange(self, nums: List[int], start: int, end: int) -> int:
        if end == start:
            return nums[start]
        
        prev_max = nums[start]
        curr_max = max(nums[start], nums[start + 1])
        
        for i in range(start + 2, end + 1):
            temp = curr_max
            curr_max = max(prev_max + nums[i], curr_max)
            prev_max = temp
        
        return curr_max

2维DP

class Solution:
    def rob(self, nums: List[int]) -> int:
        if len(nums) < 3:
            return max(nums)

        # 情况二：不抢劫第一个房屋
        result1 = self.robRange(nums[:-1])

        # 情况三：不抢劫最后一个房屋
        result2 = self.robRange(nums[1:])

        return max(result1, result2)

    def robRange(self, nums):
        dp = [[0, 0] for _ in range(len(nums))]
        dp[0][1] = nums[0]

        for i in range(1, len(nums)):
            dp[i][0] = max(dp[i - 1])
            dp[i][1] = dp[i - 1][0] + nums[i]

        return max(dp[-1])

优化版

class Solution:
    def rob(self, nums: List[int]) -> int:
        if not nums:  # 如果没有房屋，返回0
            return 0

        if len(nums) == 1:  # 如果只有一个房屋，返回该房屋的金额
            return nums[0]

        # 情况二：不抢劫第一个房屋
        prev_max = 0  # 上一个房屋的最大金额
        curr_max = 0  # 当前房屋的最大金额
        for num in nums[1:]:
            temp = curr_max  # 临时变量保存当前房屋的最大金额
            curr_max = max(prev_max + num, curr_max)  # 更新当前房屋的最大金额
            prev_max = temp  # 更新上一个房屋的最大金额
        result1 = curr_max

        # 情况三：不抢劫最后一个房屋
        prev_max = 0  # 上一个房屋的最大金额
        curr_max = 0  # 当前房屋的最大金额
        for num in nums[:-1]:
            temp = curr_max  # 临时变量保存当前房屋的最大金额
            curr_max = max(prev_max + num, curr_max)  # 更新当前房屋的最大金额
            prev_max = temp  # 更新上一个房屋的最大金额
        result2 = curr_max

        return max(result1, result2)

Go：

// 打家劫舍Ⅱ 动态规划
// 时间复杂度O(n) 空间复杂度O(n)
func rob(nums []int) int {
    // 如果长度为0或1，那么有没有环的限制都一样
    if len(nums) <= 1 {
        return robWithoutCircle(nums)
    }

    // 否则，去头或去尾，取最大
    res1 := robWithoutCircle(nums[:len(nums)-1])
    res2 := robWithoutCircle(nums[1:])

    return max(res1, res2)
}

// 原始的打家劫舍版
func robWithoutCircle(nums []int) int {
    switch len(nums) {
        case 0: return 0
        case 1: return nums[0]
    }
    dp := make([]int, len(nums))
    dp[0]=nums[0]
    dp[1] = max(nums[0], nums[1])

    for i:=2; i<len(nums); i++ {
        dp[i] = max(dp[i-1], dp[i-2]+nums[i])
    }

    return dp[len(nums)-1]

}

func max(a, b int ) int {
    if a>b {
        return a
    }
    return b
}

JavaScript:

var rob = function(nums) {
  const n = nums.length
  if (n === 0) return 0
  if (n === 1) return nums[0]
  const result1 = robRange(nums, 0, n - 2)
  const result2 = robRange(nums, 1, n - 1)
  return Math.max(result1, result2)
};

const robRange = (nums, start, end) => {
  if (end === start) return nums[start]
  const dp = Array(nums.length).fill(0)
  dp[start] = nums[start]
  dp[start + 1] = Math.max(nums[start], nums[start + 1])
  for (let i = start + 2; i <= end; i++) {
    dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1])
  }
  return dp[end]
}

TypeScript：

function rob(nums: number[]): number {
    const length: number = nums.length;
    if (length === 0) return 0;
    if (length === 1) return nums[0];
    return Math.max(robRange(nums, 0, length - 2),
        robRange(nums, 1, length - 1));
};
function robRange(nums: number[], start: number, end: number): number {
    if (start === end) return nums[start];
    const dp: number[] = [];
    dp[start] = nums[start];
    dp[start + 1] = Math.max(nums[start], nums[start + 1]);
    for (let i = start + 2; i <= end; i++) {
        dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
    }
    return dp[end];
}

C

#define max(a, b) ((a) > (b) ? (a) : (b))

// 198.打家劫舍的逻辑
int robRange(int* nums, int start, int end, int numsSize) {
    if (end == start) return nums[start];
    int dp[numsSize];
    dp[start] = nums[start];
    dp[start + 1] = max(nums[start], nums[start + 1]);
    for (int i = start + 2; i <= end; i++) {
        dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
    }
    return dp[end];
}

int rob(int* nums, int numsSize) {
    if (numsSize == 0) return 0;
    if (numsSize == 1) return nums[0];
    int result1 = robRange(nums, 0, numsSize - 2, numsSize); // 情况二
    int result2 = robRange(nums, 1, numsSize - 1, numsSize); // 情况三
    return max(result1, result2);
}

Rust:

impl Solution {
    pub fn rob(nums: Vec<i32>) -> i32 {
        match nums.len() {
            1 => nums[0],
            _ => Self::rob_range(&nums, 0, nums.len() - 2).max(Self::rob_range(
                &nums,
                1,
                nums.len() - 1,
            )),
        }
    }

    pub fn rob_range(nums: &Vec<i32>, start: usize, end: usize) -> i32 {
        if start == end {
            return nums[start];
        }
        let mut dp = vec![0; nums.len()];
        dp[start] = nums[start];
        dp[start + 1] = nums[start].max(nums[start + 1]);
        for i in start + 2..=end {
            dp[i] = dp[i - 1].max(dp[i - 2] + nums[i]);
        }
        dp[end]
    }
}