Skip to content

Latest commit

 

History

History
354 lines (256 loc) · 10.9 KB

0096.不同的二叉搜索树.md

File metadata and controls

354 lines (256 loc) · 10.9 KB
Raw

参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

96.不同的二叉搜索树

力扣题目链接

给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

示例:

算法公开课

《代码随想录》算法视频公开课：动态规划找到子状态之间的关系很重要！| LeetCode：96.不同的二叉搜索树，相信结合视频再看本篇题解，更有助于大家对本题的理解。

思路

这道题目描述很简短，但估计大部分同学看完都是懵懵的状态，这得怎么统计呢？

关于什么是二叉搜索树，我们之前在讲解二叉树专题的时候已经详细讲解过了，也可以看看这篇二叉树：二叉搜索树登场！再回顾一波。

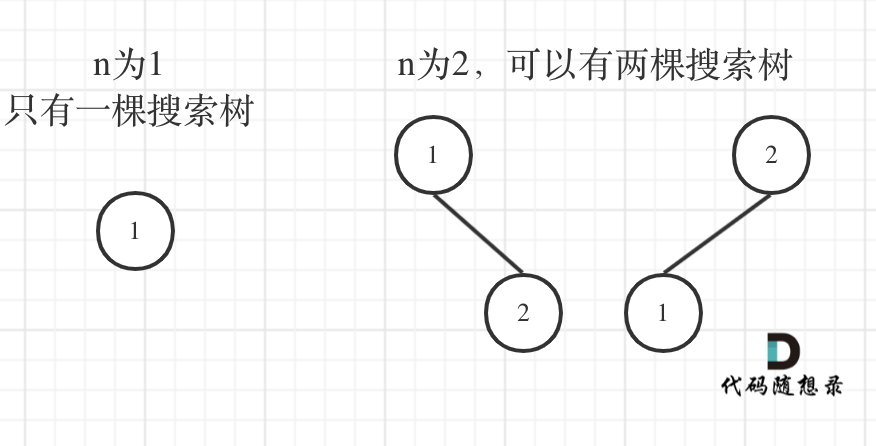
了解了二叉搜索树之后，我们应该先举几个例子，画画图，看看有没有什么规律，如图：

96.不同的二叉搜索树

n为1的时候有一棵树，n为2有两棵树，这个是很直观的。

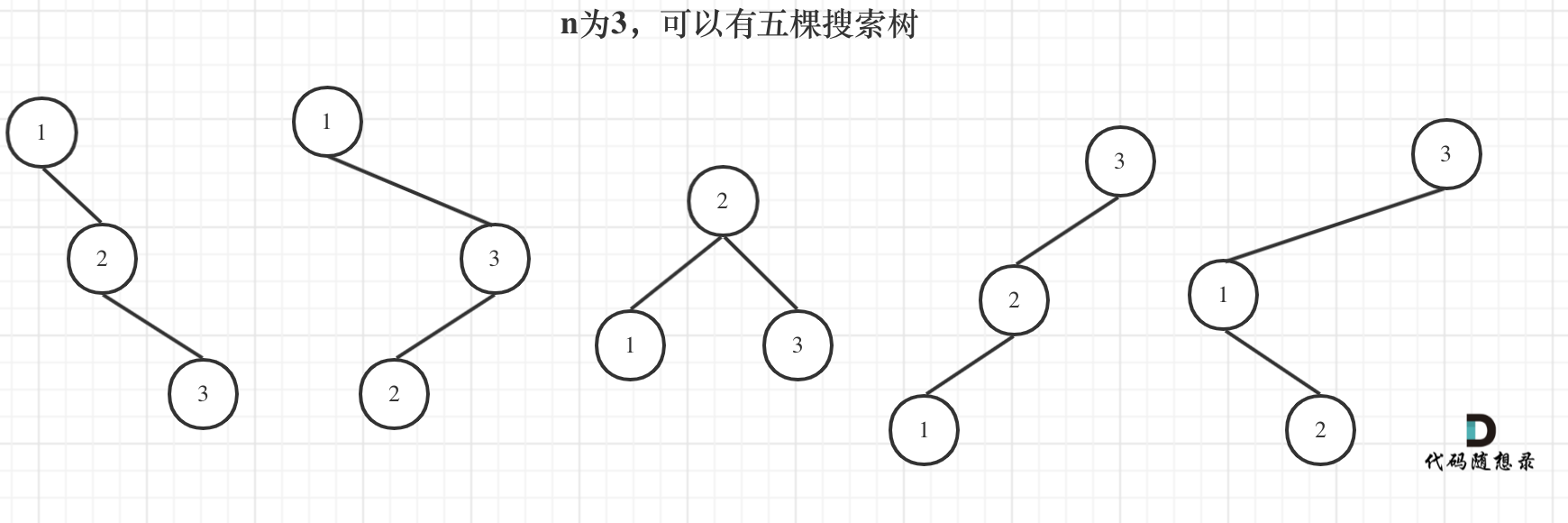
96.不同的二叉搜索树1

来看看n为3的时候，有哪几种情况。

当1为头结点的时候，其右子树有两个节点，看这两个节点的布局，是不是和 n 为2的时候两棵树的布局是一样的啊！

（可能有同学问了，这布局不一样啊，节点数值都不一样。别忘了我们就是求不同树的数量，并不用把搜索树都列出来，所以不用关心其具体数值的差异）

当3为头结点的时候，其左子树有两个节点，看这两个节点的布局，是不是和n为2的时候两棵树的布局也是一样的啊！

当2为头结点的时候，其左右子树都只有一个节点，布局是不是和n为1的时候只有一棵树的布局也是一样的啊！

发现到这里，其实我们就找到了重叠子问题了，其实也就是发现可以通过dp[1] 和 dp[2] 来推导出来dp[3]的某种方式。

思考到这里，这道题目就有眉目了。

dp[3]，就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量

元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量

元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量

元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量

有2个元素的搜索树数量就是dp[2]。

有1个元素的搜索树数量就是dp[1]。

有0个元素的搜索树数量就是dp[0]。

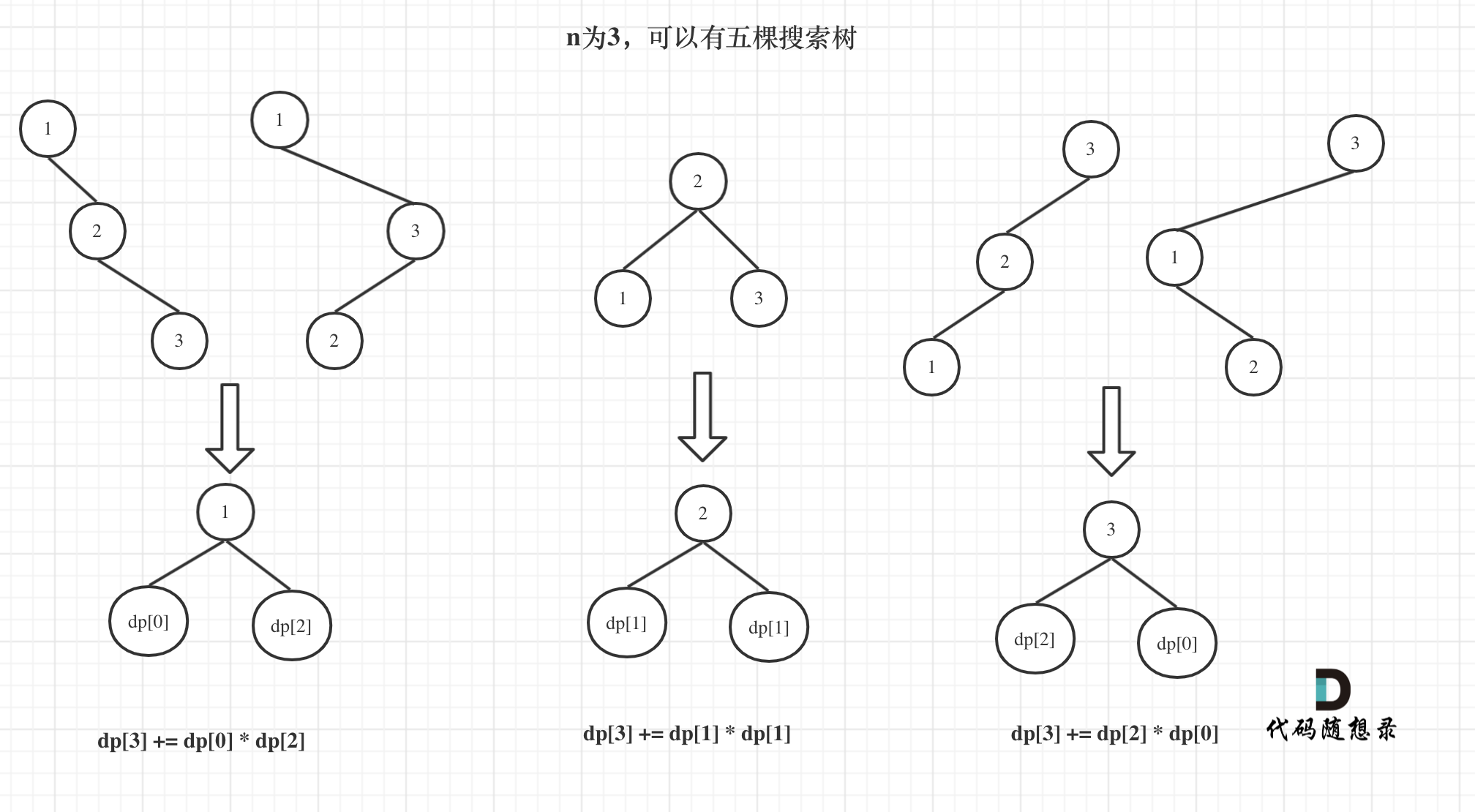
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]

如图所示：

96.不同的二叉搜索树2

此时我们已经找到递推关系了，那么可以用动规五部曲再系统分析一遍。

  1. 确定dp数组（dp table）以及下标的含义

dp[i] ： 1到i为节点组成的二叉搜索树的个数为dp[i]。

也可以理解是i个不同元素节点组成的二叉搜索树的个数为dp[i] ，都是一样的。

以下分析如果想不清楚，就来回想一下dp[i]的定义

  1. 确定递推公式

在上面的分析中，其实已经看出其递推关系， dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]

j相当于是头结点的元素，从1遍历到i为止。

所以递推公式：dp[i] += dp[j - 1] * dp[i - j]; ，j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量

  1. dp数组如何初始化

初始化，只需要初始化dp[0]就可以了，推导的基础，都是dp[0]。

那么dp[0]应该是多少呢？

从定义上来讲，空节点也是一棵二叉树，也是一棵二叉搜索树，这是可以说得通的。

从递归公式上来讲，dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0，也需要dp[以j为头结点左子树节点数量] = 1， 否则乘法的结果就都变成0了。

所以初始化dp[0] = 1

  1. 确定遍历顺序

首先一定是遍历节点数，从递归公式：dp[i] += dp[j - 1] * dp[i - j]可以看出，节点数为i的状态是依靠 i之前节点数的状态。

那么遍历i里面每一个数作为头结点的状态，用j来遍历。

代码如下：

for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= i; j++) {
        dp[i] += dp[j - 1] * dp[i - j];
    }
}
  1. 举例推导dp数组

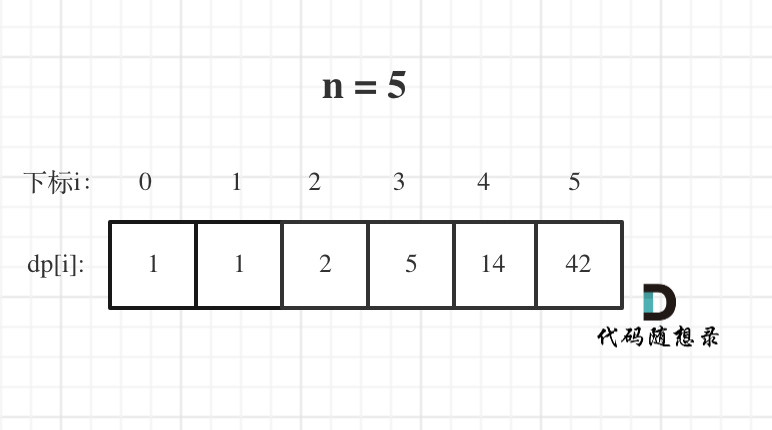
n为5时候的dp数组状态如图：

96.不同的二叉搜索树3

当然如果自己画图举例的话，基本举例到n为3就可以了，n为4的时候，画图已经比较麻烦了。

我这里列到了n为5的情况，是为了方便大家 debug代码的时候，把dp数组打出来，看看哪里有问题。

综上分析完毕，C++代码如下：

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n + 1);
        dp[0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
};
  • 时间复杂度：$O(n^2)$
  • 空间复杂度：$O(n)$

大家应该发现了，我们分析了这么多，最后代码却如此简单！

总结

这道题目虽然在力扣上标记是中等难度，但可以算是困难了！

首先这道题想到用动规的方法来解决，就不太好想，需要举例，画图，分析，才能找到递推的关系。

然后难点就是确定递推公式了，如果把递推公式想清楚了，遍历顺序和初始化，就是自然而然的事情了。

可以看出我依然还是用动规五部曲来进行分析，会把题目的方方面面都覆盖到！

而且具体这五部分析是我自己平时总结的经验，找不出来第二个的，可能过一阵子 其他题解也会有动规五部曲了。

当时我在用动规五部曲讲解斐波那契的时候，一些录友和我反应，感觉讲复杂了。

其实当时我一直强调简单题是用来练习方法论的，并不能因为简单我就代码一甩，简单解释一下就完事了。

可能当时一些同学不理解，现在大家应该感受方法论的重要性了，加油💪

其他语言版本

Java

class Solution {
    public int numTrees(int n) {
        //初始化 dp 数组
        int[] dp = new int[n + 1];
        //初始化0个节点和1个节点的情况
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                //对于第i个节点，需要考虑1作为根节点直到i作为根节点的情况，所以需要累加
                //一共i个节点，对于根节点j时,左子树的节点个数为j-1，右子树的节点个数为i-j
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
}

Python

class Solution:
    def numTrees(self, n: int) -> int:
        dp = [0] * (n + 1)  # 创建一个长度为n+1的数组，初始化为0
        dp[0] = 1  # 当n为0时，只有一种情况，即空树，所以dp[0] = 1
        for i in range(1, n + 1):  # 遍历从1到n的每个数字
            for j in range(1, i + 1):  # 对于每个数字i，计算以i为根节点的二叉搜索树的数量
                dp[i] += dp[j - 1] * dp[i - j]  # 利用动态规划的思想，累加左子树和右子树的组合数量
        return dp[n]  # 返回以1到n为节点的二叉搜索树的总数量

Go

func numTrees(n int)int{
	dp := make([]int, n+1)
	dp[0] = 1
	for i := 1; i <= n; i++ {
		for j := 1; j <= i; j++ {
			dp[i] += dp[j-1] * dp[i-j]
		}
	}
	return dp[n]
}

Javascript

const numTrees =(n) => {
    let dp = new Array(n+1).fill(0);
    dp[0] = 1;
    dp[1] = 1;

    for(let i = 2; i <= n; i++) {
        for(let j = 1; j <= i; j++) {
            dp[i] += dp[j-1] * dp[i-j];
        }
    }

    return dp[n];
};

TypeScript

function numTrees(n: number): number {
    /**
        dp[i]: i个节点对应的种树
        dp[0]: -1; 无意义；
        dp[1]: 1;
        ...
        dp[i]: 2 * dp[i - 1] +
            (dp[1] * dp[i - 2] + dp[2] * dp[i - 3] + ... + dp[i - 2] * dp[1]); 从1加到i-2
     */
    const dp: number[] = [];
    dp[0] = -1; // 表示无意义
    dp[1] = 1;
    for (let i = 2; i <= n; i++) {
        dp[i] = 2 * dp[i - 1];
        for (let j = 1, end = i - 1; j < end; j++) {
            dp[i] += dp[j] * dp[end - j];
        }
    }
    return dp[n];
};

Rust

impl Solution {
    pub fn num_trees(n: i32) -> i32 {
        let n = n as usize;
        let mut dp = vec![0; n + 1];
        dp[0] = 1;
        for i in 1..=n {
            for j in 1..=i {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        dp[n]
    }
}

C

//开辟dp数组
int *initDP(int n) {
    int *dp = (int *)malloc(sizeof(int) * (n + 1));
    int i;
    for(i = 0; i <= n; ++i)
        dp[i] = 0;
    return dp;
}

int numTrees(int n){
    //开辟dp数组
    int *dp = initDP(n);
    //将dp[0]设为1
    dp[0] = 1;

    int i, j;
    for(i = 1; i <= n; ++i) {
        for(j = 1; j <= i; ++j) {
            //递推公式：dp[i] = dp[i] + 根为j时左子树种类个数 * 根为j时右子树种类个数
            dp[i] += dp[j - 1] * dp[i - j];
        }
    }

    return dp[n];
}

Scala

object Solution {
  def numTrees(n: Int): Int = {
    var dp = new Array[Int](n + 1)
    dp(0) = 1
    for (i <- 1 to n) {
      for (j <- 1 to i) {
        dp(i) += dp(j - 1) * dp(i - j)
      }
    }
    dp(n)
  }
}

C#

public class Solution
{
    public int NumTrees(int n)
    {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= i; j++)
            {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
}