接下来我们来讲一下并查集,首先当然是并查集理论基础。
首先要知道并查集可以解决什么问题呢?
并查集常用来解决连通性问题。
大白话就是当我们需要判断两个元素是否在同一个集合里的时候,我们就要想到用并查集。
并查集主要有两个功能:
- 将两个元素添加到一个集合中。
- 判断两个元素在不在同一个集合
接下来围绕并查集的这两个功能来展开讲解。
从代码层面,我们如何将两个元素添加到同一个集合中呢。
此时有录友会想到:可以把他放到同一个数组里或者set 或者 map 中,这样就表述两个元素在同一个集合。
那么问题来了,对这些元素分门别类,可不止一个集合,可能是很多集合,成百上千,那么要定义这么多个数组吗?
有录友想,那可以定义一个二维数组。
但如果我们要判断两个元素是否在同一个集合里的时候 我们又能怎么办? 只能把而二维数组都遍历一遍。
而且每当想添加一个元素到某集合的时候,依然需要把把二维数组组都遍历一遍,才知道要放在哪个集合里。
这仅仅是一个粗略的思路,如果沿着这个思路去实现代码,非常复杂,因为管理集合还需要很多逻辑。
那么我们来换一个思路来看看。
我们将三个元素A,B,C (分别是数字)放在同一个集合,其实就是将三个元素连通在一起,如何连通呢。
只需要用一个一维数组来表示,即:father[A] = B,father[B] = C 这样就表述 A 与 B 与 C连通了(有向连通图)。
代码如下:
// 将v,u 这条边加入并查集
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
father[v] = u;
}可能有录友想,这样我可以知道 A 连通 B,因为 A 是索引下标,根据 father[A]的数值就知道 A 连通 B。那怎么知道 B 连通 A呢?
我们的目的是判断这三个元素是否在同一个集合里,知道 A 连通 B 就已经足够了。
这里要讲到寻根思路,只要 A ,B,C 在同一个根下就是同一个集合。
给出A元素,就可以通过 father[A] = B,father[B] = C,找到根为 C。
给出B元素,就可以通过 father[B] = C,找到根也为为 C,说明 A 和 B 是在同一个集合里。 大家会想第一段代码里find函数是如何实现的呢?其实就是通过数组下标找到数组元素,一层一层寻根过程,代码如下:
// 并查集里寻根的过程
int find(int u) {
if (u == father[u]) return u; // 如果根就是自己,直接返回
else return find(father[u]); // 如果根不是自己,就根据数组下标一层一层向下找
}
如何表示 C 也在同一个元素里呢? 我们需要 father[C] = C,即C的根也为C,这样就方便表示 A,B,C 都在同一个集合里了。
所以father数组初始化的时候要 father[i] = i,默认自己指向自己。
代码如下:
// 并查集初始化
void init() {
for (int i = 0; i < n; ++i) {
father[i] = i;
}
}最后我们如何判断两个元素是否在同一个集合里,如果通过 find函数 找到 两个元素属于同一个根的话,那么这两个元素就是同一个集合,代码如下:
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}在实现 find 函数的过程中,我们知道,通过递归的方式,不断获取father数组下标对应的数值,最终找到这个集合的根。
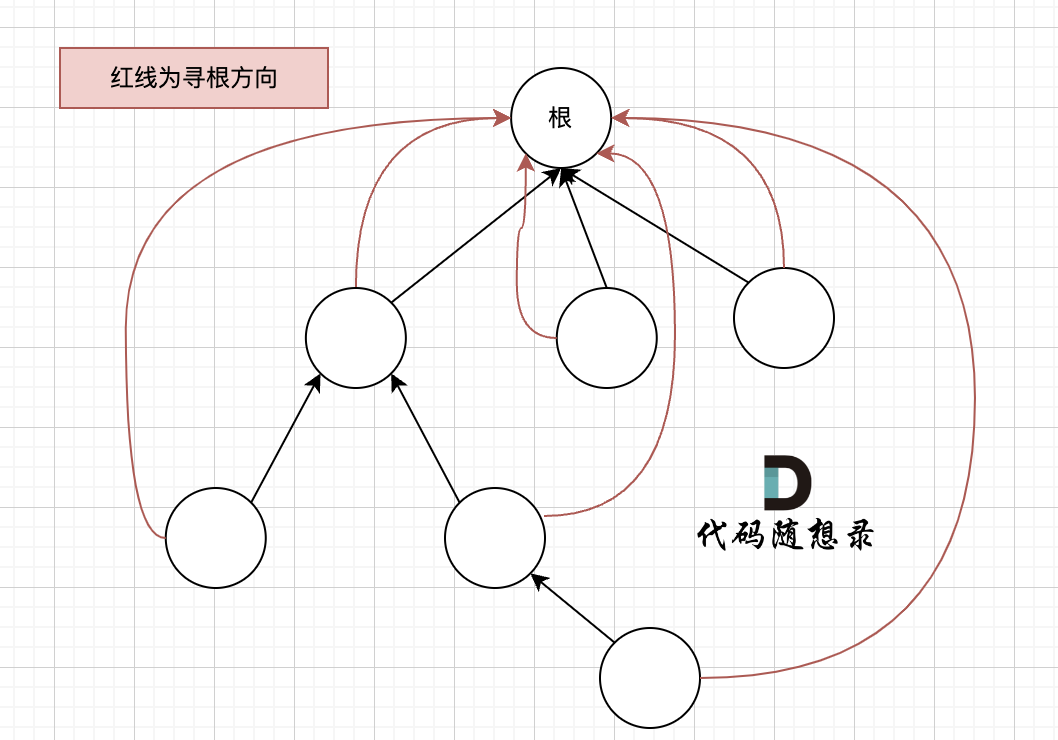
搜索过程像是一个多叉树中从叶子到根节点的过程,如图:
如果这棵多叉树高度很深的话,每次find函数 去寻找根的过程就要递归很多次。
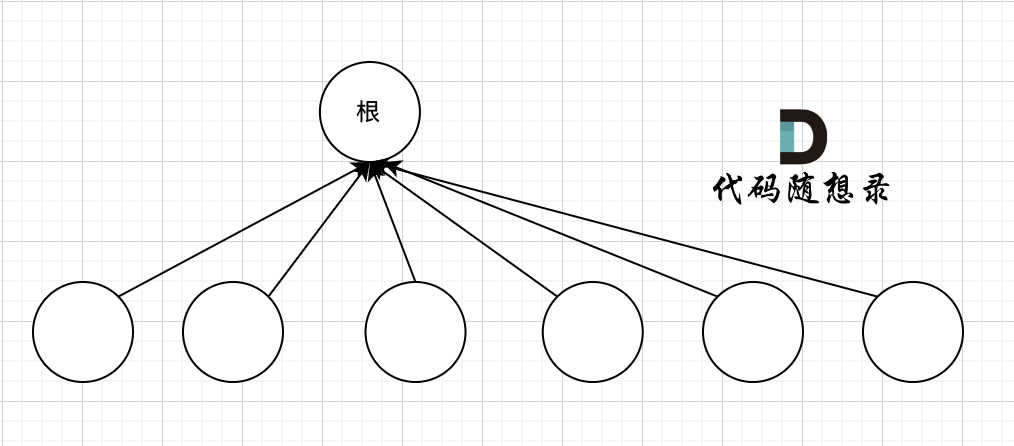
我们的目的只需要知道这些节点在同一个根下就可以,所以对这棵多叉树的构造只需要这样就可以了,如图:
除了根节点其他所有节点都挂载根节点下,这样我们在寻根的时候就很快,只需要一步,
如果我们想达到这样的效果,就需要 路径压缩,将非根节点的所有节点直接指向根节点。 那么在代码层面如何实现呢?
我们只需要在递归的过程中,让 father[u] 接住 递归函数 find(father[u]) 的返回结果。
因为 find 函数向上寻找根节点,father[u] 表述 u 的父节点,那么让 father[u] 直接获取 find函数 返回的根节点,这样就让节点 u 的父节点 变成根节点。
代码如下,注意看注释,路径压缩就一行代码:
// 并查集里寻根的过程
int find(int u) {
if (u == father[u]) return u;
else return father[u] = find(father[u]); // 路径压缩
}以上代码在C++中,可以用三元表达式来精简一下,代码如下:
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]);
}
相信不少录友在学习并查集的时候,对上面这三行代码实现的 find函数 很熟悉,但理解上却不够深入,仅仅知道这行代码很好用,不知道这里藏着路径压缩的过程。
所以对于算法初学者来说,直接看精简代码学习是不太友好的,往往忽略了很多细节。
那么此时并查集的模板就出来了, 整体模板C++代码如下:
int n = 1005; // n根据题目中节点数量而定,一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构
// 并查集初始化
void init() {
for (int i = 0; i < n; ++i) {
father[i] = i;
}
}
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return ; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
father[v] = u;
}通过模板,我们可以知道,并查集主要有三个功能。
- 寻找根节点,函数:find(int u),也就是判断这个节点的祖先节点是哪个
- 将两个节点接入到同一个集合,函数:join(int u, int v),将两个节点连在同一个根节点上
- 判断两个节点是否在同一个集合,函数:isSame(int u, int v),就是判断两个节点是不是同一个根节点
这里估计有录友会想,模板中的 join 函数里的这段代码:
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return ; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
与 isSame 函数的实现是不是重复了? 如果抽象一下呢,代码如下:
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
if (isSame) return ; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
father[v] = u;
}这样写可以吗? 好像看出去没问题,而且代码更精简了。
其实这么写是有问题的,在join函数中 我们需要寻找 u 和 v 的根,然后再进行连线在一起,而不是直接 用 u 和 v 连线在一起。
举一个例子:
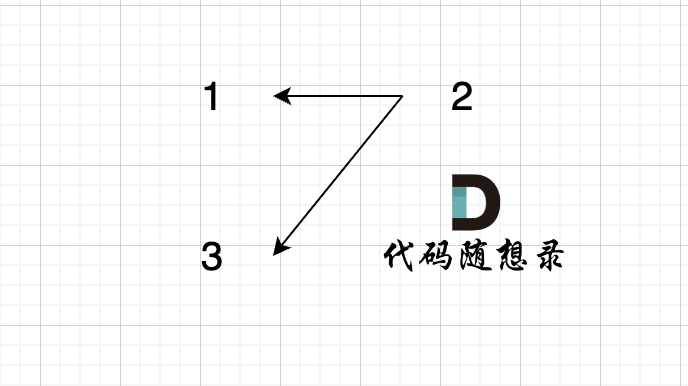
join(1, 2);
join(3, 2);
此时构成的图是这样的:
此时问 1,3是否在同一个集合,我们调用 join(1, 2); join(3, 2); 很明显本意要表示 1,3是在同一个集合。
但我们来看一下代码逻辑,当我们调用 isSame(1, 3)的时候,find(1) 返回的是1,find(3)返回的是3。 return 1 == 3 返回的是false,代码告诉我们 1 和 3 不在同一个集合,这明显不符合我们的预期,所以问题出在哪里?
问题出在我们精简的代码上,即 join 函数 一定要先 通过find函数寻根再进行关联。
如果find函数是这么实现,再来看一下逻辑过程。
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return ; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
father[v] = u;
}分别将 这两对元素加入集合。
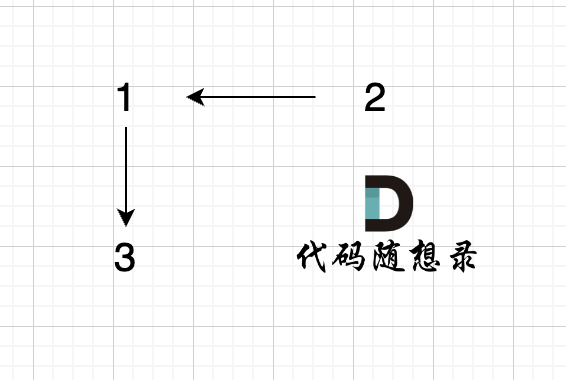
join(1, 2);
join(3, 2);当执行join(3, 2)的时候,会先通过find函数寻找 3的根为3,2的根为1 (第一个join(1, 2),将2的根设置为1),所以最后是将1 指向 3。
构成的图是这样的:
因为在join函数里,我们有find函数进行寻根的过程,这样就保证元素 1,2,3在这个有向图里是强连通的。
此时我们在调用 isSame(1, 3)的时候,find(1) 返回的是3,find(3) 返回的也是3,return 3 == 3 返回的是true,即告诉我们 元素 1 和 元素3 是 在同一个集合里的。
(凸显途径合并的过程,每一个join都要画图)
不少录友在接触并查集模板之后,用起来很娴熟,因为模板确实相对固定,但是对并查集内部数据组织方式以及如何判断是否是同一个集合的原理很模糊。
通过以上讲解之后,我在带大家一步一步去画一下,并查集内部数据连接方式。
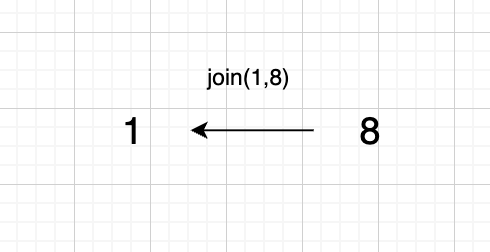
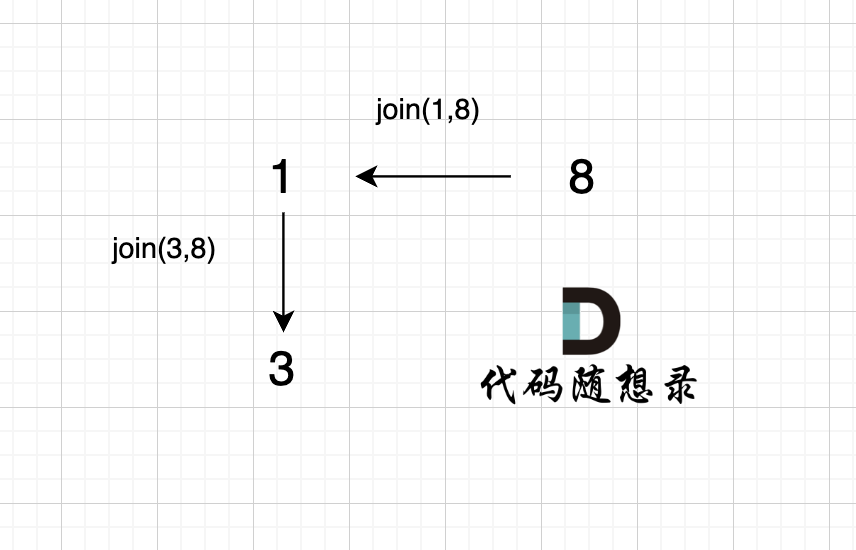
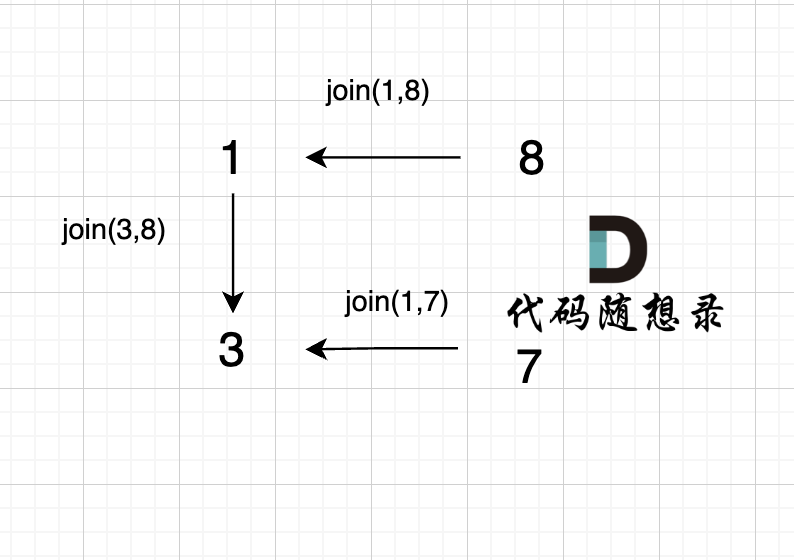
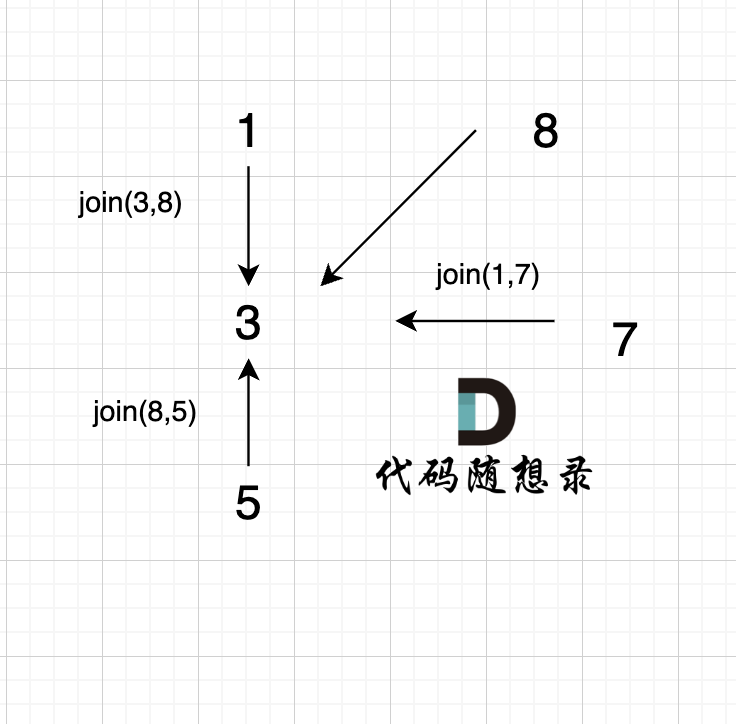
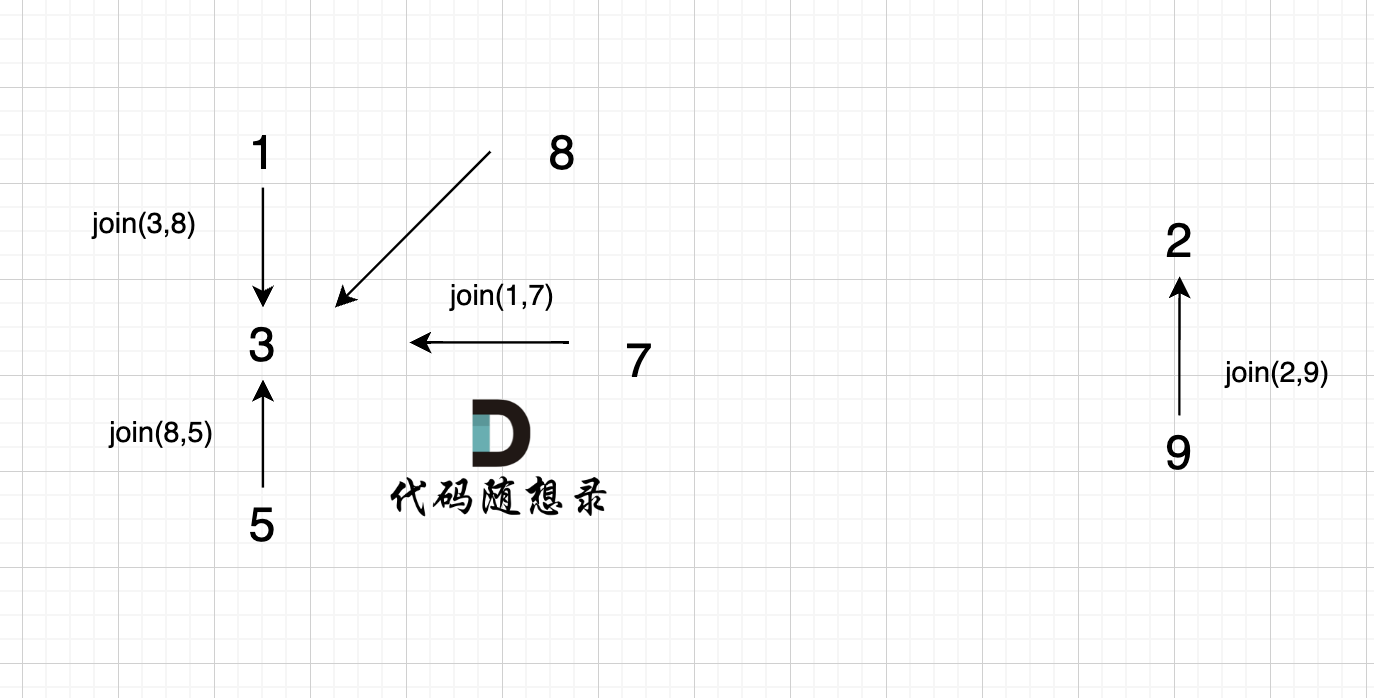
1、join(1, 8);
2、join(3, 8);
有录友可能想,join(3, 8) 在图中为什么 将 元素1 连向元素 3 而不是将 元素 8 连向 元素 3 呢?
这一点 我在 「常见误区」标题下已经详细讲解了,因为在join(int u, int v)函数里 要分别对 u 和 v 寻根之后再进行关联。
3、join(1, 7);
4、join(8, 5);
这里8的根是3,那么 5 应该指向 8 的根 3,这里的原因,我们在上面「常见误区」已经讲过了。 但 为什么 图中 8 又直接指向了 3 了呢?
因为路经压缩了
即如下代码在寻找根的过程中,会有路径压缩,减少 下次查询的路径长度。
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}
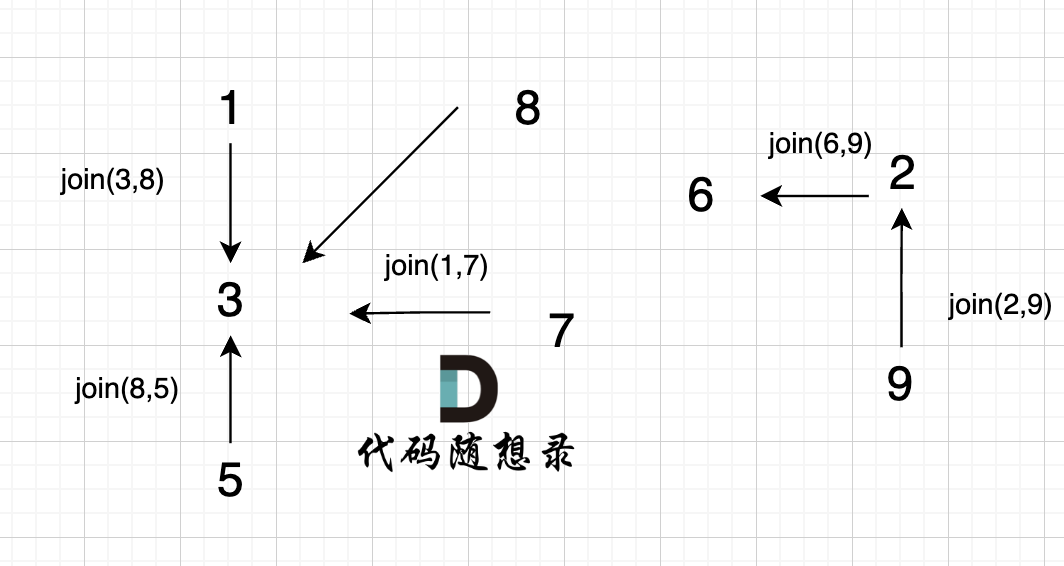
5、join(2, 9);
6、join(6, 9);
这里为什么是 2 指向了 6,因为 9的根为 2,所以用2指向6。
大家看懂这个有向图后,相信应该知道如下函数的返回值了。
cout << isSame(8, 7) << endl;
cout << isSame(7, 2) << endl;返回值分别如下,表示,8 和 7 是同一个集合,而 7 和 2 不是同一个集合。
true
false
在「路径压缩」讲解中,我们知道如何靠压缩路径来缩短查询根节点的时间。
其实还有另一种方法:按秩(rank)合并。
rank表示树的高度,即树中结点层次的最大值。
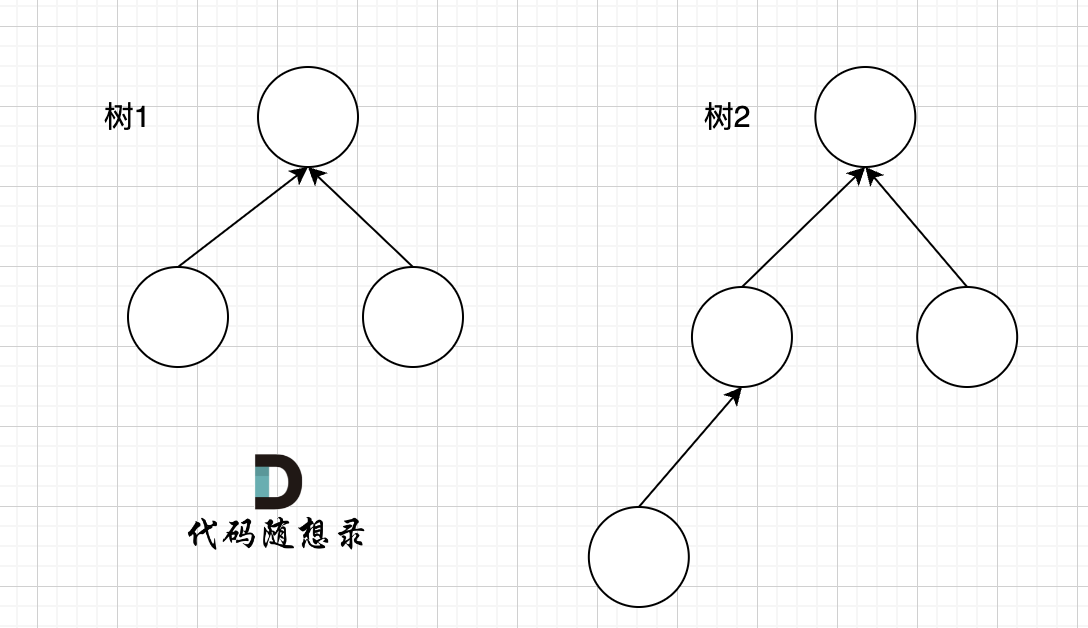
例如两个集合(多叉树)需要合并,如图所示:
树1 rank 为2,树2 rank 为 3。那么合并两个集合,是 树1 合入 树2,还是 树2 合入 树1呢?
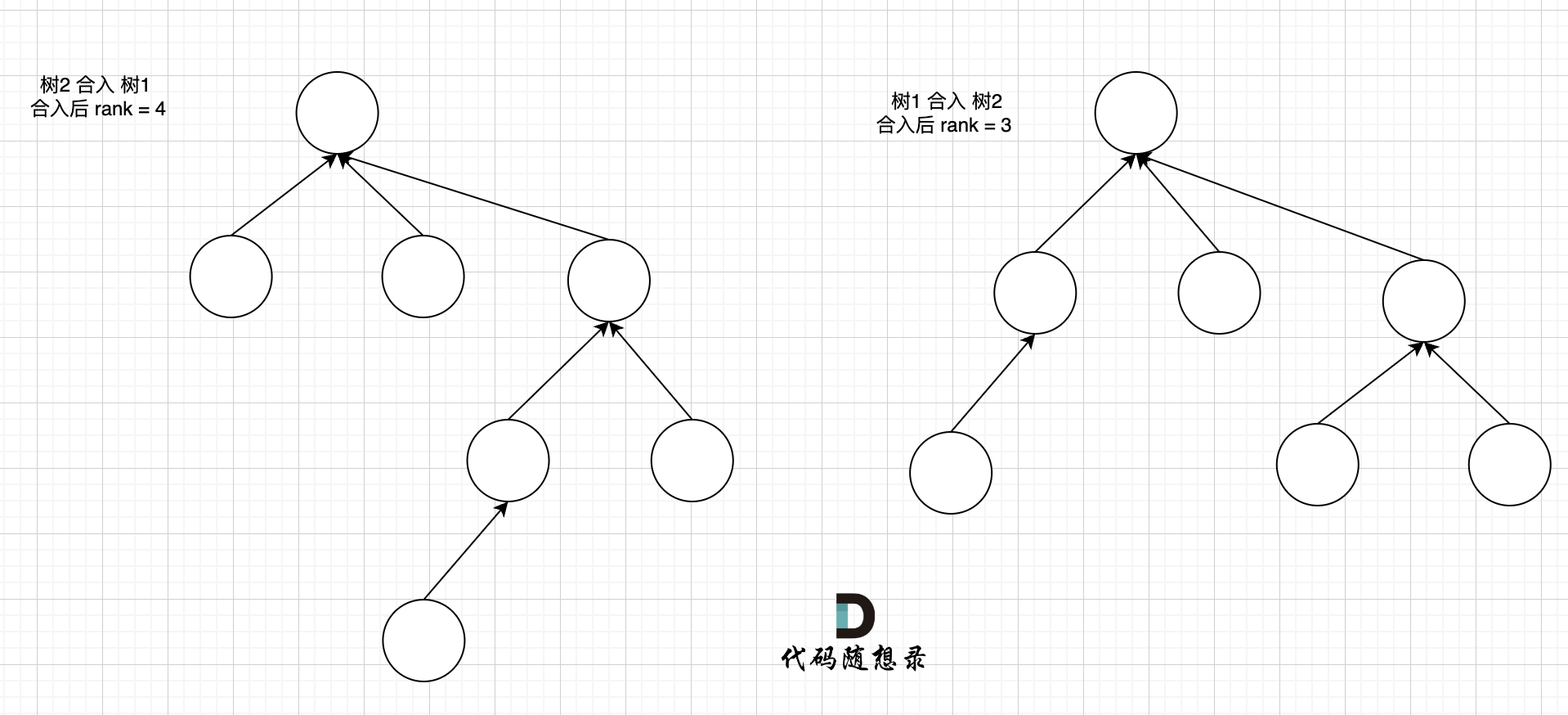
我们来看两个不同方式合入的效果。
这里可以看出,树2 合入 树1 会导致整棵树的高度变的更高,而 树1 合入 树2 整棵树的高度 和 树2 保持一致。
所以在 join函数中如何合并两棵树呢?
一定是 rank 小的树合入 到 rank大 的树,这样可以保证最后合成的树rank 最小,降低在树上查询的路径长度。
按秩合并的代码如下:
int n = 1005; // n根据题目中节点数量而定,一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构
vector<int> rank = vector<int> (n, 1); // 初始每棵树的高度都为1
// 并查集初始化
void init() {
for (int i = 0; i < n; ++i) {
father[i] = i;
rank[i] = 1; // 也可以不写
}
}
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : find(father[u]);// 注意这里不做路径压缩
}
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (rank[u] <= rank[v]) father[u] = v; // rank小的树合入到rank大的树
else father[v] = u;
if (rank[u] == rank[v] && u != v) rank[v]++; // 如果两棵树高度相同,则v的高度+1,因为上面 if (rank[u] <= rank[v]) father[u] = v; 注意是 <=
}可以注意到在上面的模板代码中,我是没有做路径压缩的,因为一旦做路径压缩,rank记录的高度就不准了,根据rank来判断如何合并就没有意义。
也可以在 路径压缩的时候,再去实时修生rank的数值,但这样在代码实现上麻烦了不少,关键是收益很小。
其实我们在优化并查集查询效率的时候,只用路径压缩的思路就够了,不仅代码实现精简,而且效率足够高。
按秩合并的思路并没有将树形结构尽可能的扁平化,所以在整理效率上是没有路径压缩高的。
说到这里可能有录友会想,那在路径压缩的代码中,只有查询的过程 即 find 函数的执行过程中会有路径压缩,如果一直没有使用find函数,是不是相当于这棵树就没有路径压缩,导致查询效率依然很低呢?
大家可以再去回顾使用路径压缩的 并查集模板,在isSame函数 和 join函数中,我们都调用了 find 函数来进行寻根操作。
也就是说,无论使用并查集模板里哪一个函数(除了init函数),都会有路径压缩的过程,第二次访问相同节点的时候,这个节点就是直连根节点的,即 第一次访问的时候它的路径就被压缩了。
所以这里推荐大家直接使用路径压缩的并查集模板就好,但按秩合并的优化思路我依然给大家讲清楚,有助于更深一步理解并查集的优化过程。
这里对路径压缩版并查集来做分析。
空间复杂度: O(n) ,申请一个father数组。
关于时间复杂度,如果想精确表达出来需要繁琐的数学证明,就不在本篇讲解范围内了,大家感兴趣可以自己去深入研究。
这里做一个简单的分析思路。
路径压缩后的并查集时间复杂度在O(logn)与O(1)之间,且随着查询或者合并操作的增加,时间复杂度会越来越趋于O(1)。
了解到这个程度对于求职面试来说就够了。
在第一次查询的时候,相当于是n叉树上从叶子节点到根节点的查询过程,时间复杂度是logn,但路径压缩后,后面的查询操作都是O(1),而 join 函数 和 isSame函数 里涉及的查询操作也是一样的过程。
本篇我们讲解了并查集的背景、原理、两种优化方式(路径压缩,按秩合并),代码模板,常见误区,以及模拟过程。
要知道并查集解决什么问题,在什么场景下我们要想到使用并查集。
接下来进一步优化并查集的执行效率,重点介绍了路径压缩的方式,另一种方法:按秩合并,我们在 「拓展」中讲解。
通过一步一步的原理讲解,最后给出并查集的模板,所有的并查集题目都在这个模板的基础上进行操作或者适当修改。
但只给出模板还是不够的,针对大家学习并查集的常见误区,详细讲解了模板代码的细节。
为了让录友们进一步了解并查集的运行过程,我们再通过具体用例模拟一遍代码过程并画出对应的内部数据连接图(有向图)。
这里也建议大家去模拟一遍才能对并查集理解的更到位。
如果对模板代码还是有点陌生,不用担心,接下来我会讲解对应LeetCode上的并查集题目,通过一系列题目练习,大家就会感受到这套模板有多么的好用!
敬请期待 并查集题目精讲系列。