无论是哪种遍历方法，考查节点的顺序都是一样的(思考做试卷的时候，人工遍历考查顺序)。只不过有时候考查了节点，将其暂存，需要之后的过程中输出。图2：先序、中序、后序遍历节点考查顺序如图1所示，三种遍历方法(人工)得到的结果分别是：

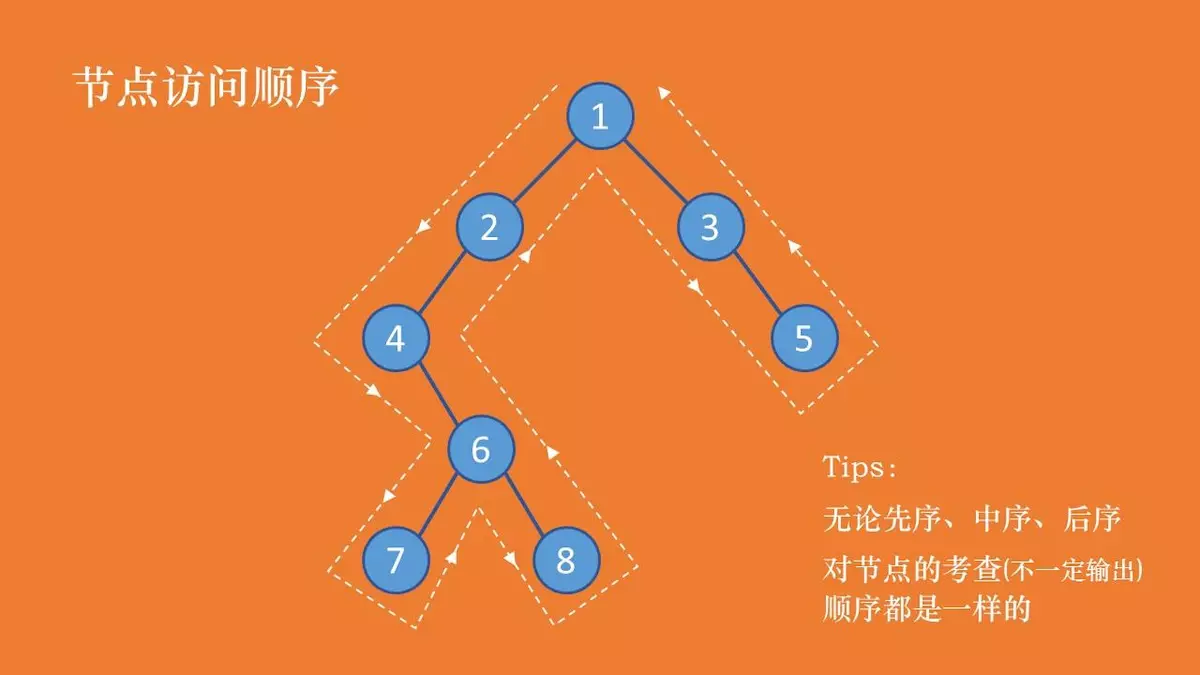
先序：1 2 4 6 7 8 3 5 中序：4 7 6 8 2 1 3 5 后序：7 8 6 4 2 5 3 1

三种遍历方法的考查顺序一致，得到的结果却不一样，原因在于： **先序：**考察到一个节点后，即刻输出该节点的值，并继续遍历其左右子树。(根左右) **中序：**考察到一个节点后，将其暂存，遍历完左子树后，再输出该节点的值，然后遍历右子树。(左根右) **后序：**考察到一个节点后，将其暂存，遍历完左右子树后，再输出该节点的值。(左右根)

下面展示了使用统一迭代写法写出三种遍历：

144. Binary Tree Preorder Traversal [Medium]

迭代写法 1

(ref: https://www.jianshu.com/p/456af5480cee)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> path = new ArrayList<>();

        Stack<TreeNode> stack = new Stack<>();
        TreeNode p = root;
        while (p != null || !stack.empty()) {
            // 访问该节点并加到 path 中（前序先访问根节点），同时继续访问该节点的左子树
            // 等到访问到叶子节点时，栈顶元素即该叶子节点
            while (p != null) {
                path.add(p.val);
                stack.push(p);
                p = p.left;
            }

            // 从栈中弹出一个节点，即拿到当前访问节点的父节点，然后把当前节点 p 置为右子树
            // 注意：上面的 while 实际上访问到叶子节点的时候已经访问了一个 leaf 节点了，
            // 即已经访问了 根 -> 左，接下来只需要访问右子树了
            if (!stack.empty()) {
                TreeNode tmp = stack.pop();
                p = tmp.right;
            }
        }
        return path;
    }

}

迭代写法 2

另一种写法，从根节点开始，每次迭代弹出当前栈顶元素，并将其孩子节点压入栈中，先压右孩子再压左孩子。在这个算法中，输出到最终结果的顺序按照 Top->Bottom 和 Left->Right，符合前序遍历的顺序。

Tips: 该写法也适用于 N 叉树的前序遍历

class Solution {
  public List<Integer> preorderTraversal(TreeNode root) {
    LinkedList<TreeNode> stack = new LinkedList<>();
    LinkedList<Integer> output = new LinkedList<>();
    if (root == null) {
      return output;
    }

    stack.add(root);
    while (!stack.isEmpty()) {
      TreeNode node = stack.pollLast();
      output.add(node.val);
      // 让左子树在栈顶，这样就可以先被遍历到
      if (node.right != null) {
        stack.add(node.right);
      }
      if (node.left != null) {
        stack.add(node.left);
      }
    }
    return output;
  }
}

94. Binary Tree Inorder Traversal [Medium]

迭代写法 1

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> path = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode p = root;

        while (p != null || !stack.empty()) {
            // 先一直访问左子树，不加到 path 中（中序需要先访问左子树才访问根节点）
            // 等到访问到叶子节点的时候，stack 上栈顶的元素即该叶子节点
            while (p != null) {
                stack.push(p);
                p = p.left;
            }

            if (!stack.empty()) {
                TreeNode tmp = stack.pop();
                path.add(tmp.val);
                p = tmp.right;
            }
        }

        return path;
    }
}

145. Binary Tree Postorder Traversal [Hard]

迭代写法 1

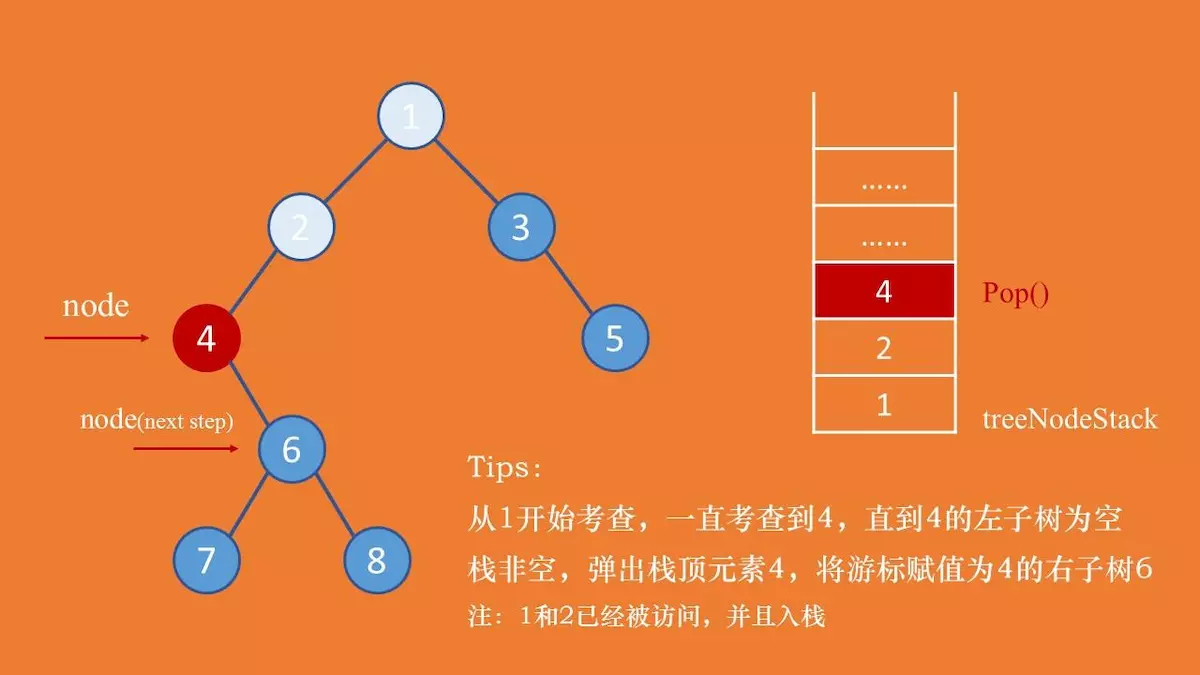
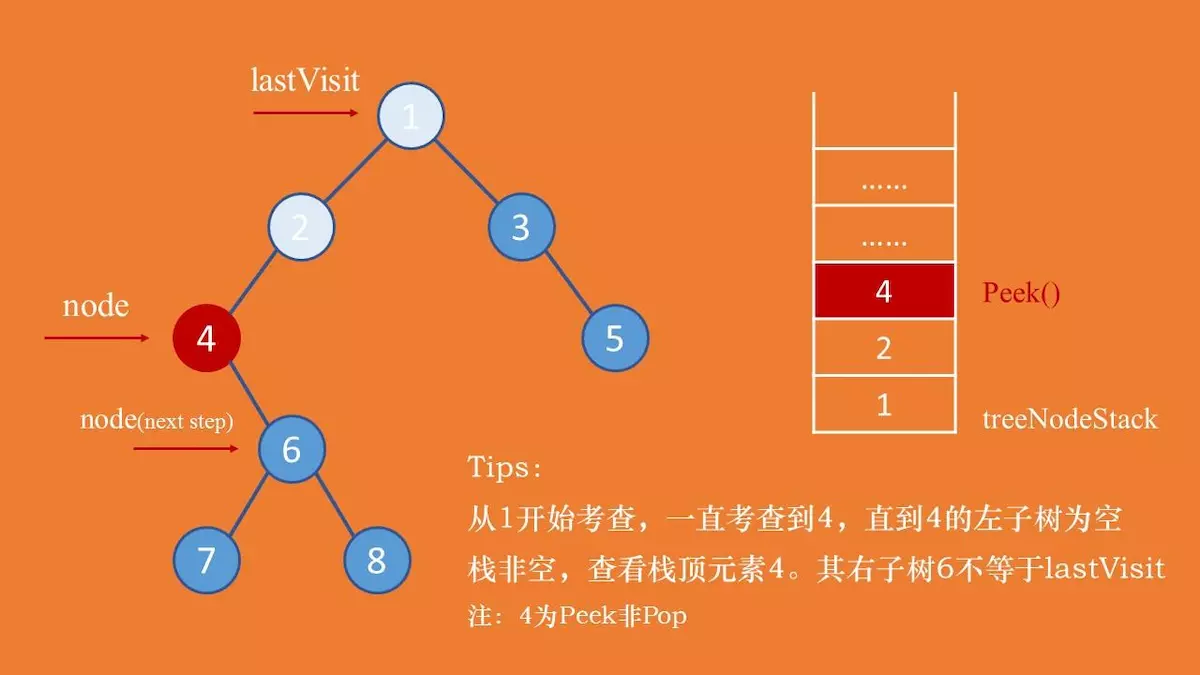
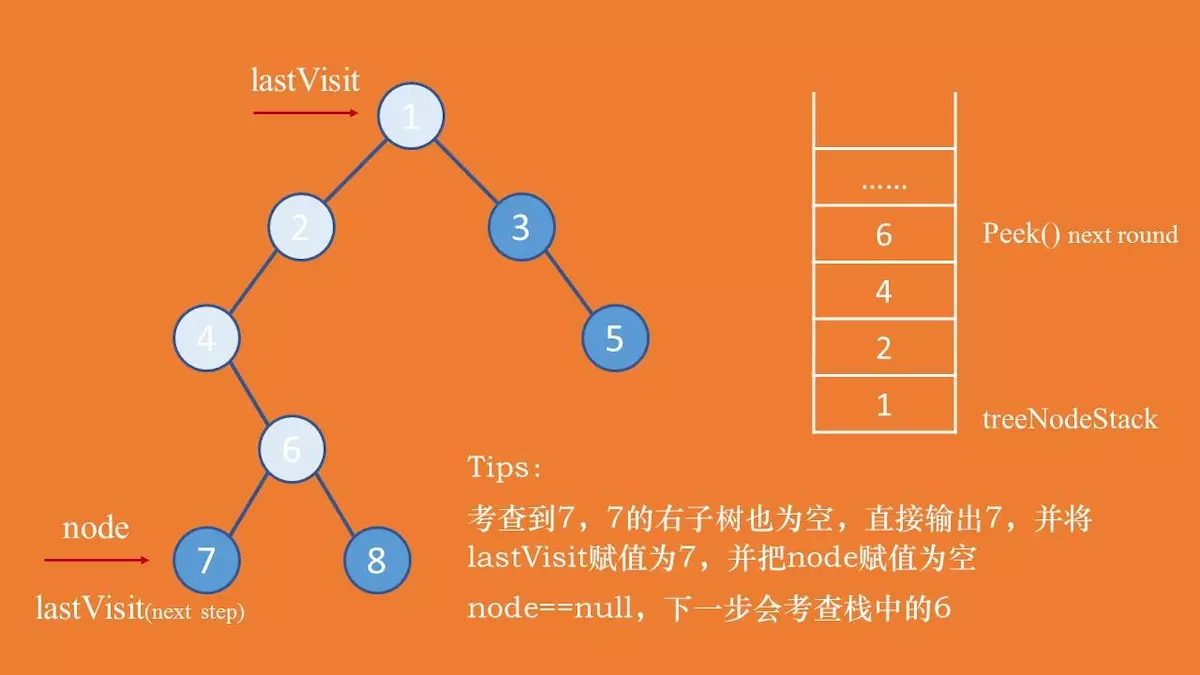
后续遍历和先序、中序遍历不太一样。后序遍历在决定是否可以输出当前节点的值的时候，需要考虑其左右子树是否都已经遍历完成。所以需要设置一个 lastVisit 游标。

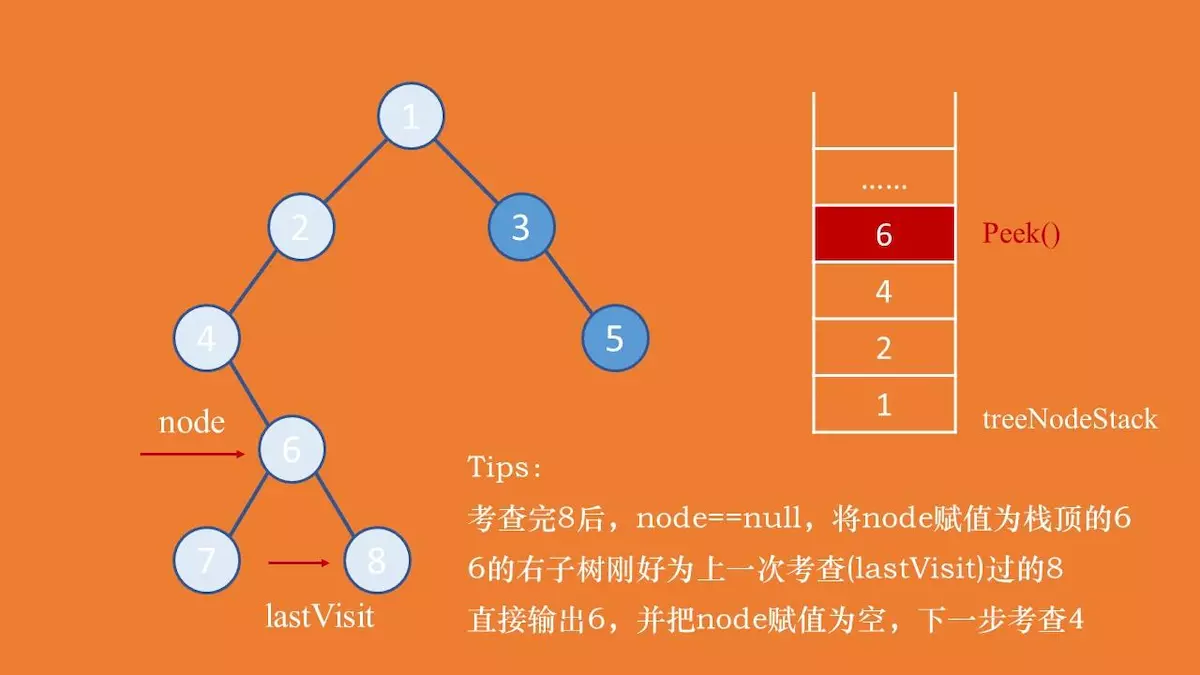
若 lastVisit 等于当前考查节点的右子树，表示该节点的左右子树都已经遍历完成，则可以输出当前节点。并把 lastVisit 节点设置成当前节点，将当前游标节点 node 设置为空，下一轮就可以访问栈顶元素。否者，需要接着考虑右子树，node = node.right。

以下考虑后序遍历中的三种情况：（图3：后序，右子树不为空，node = node.right）如图 3 所示，从节点 1 开始考查直到节点4的左子树为空。注：此时的游标节点 node = 4.left == null。此时需要从栈中**查看 Peek() **栈顶元素。发现节点 4 的右子树非空，需要接着考查右子树，4 不能输出，node = node.right。（图4：后序，左右子树都为空，直接输出）如图4所示，考查到节点 7(7.left == null，7 是从栈中弹出)，其左右子树都为空，可以直接输出 7。此时需要把 lastVisit 设置成节点 7，并把游标节点 node 设置成 null，下一轮循环的时候会考查栈中的节点 6。（图5：后序，右子树 = lastVisit，直接输出）如图 5 所示，考查完节点 8 之后(lastVisit == 节点 8)，将游标节点 node 赋值为栈顶元素 6，节点 6 的右子树正好等于节点 8。表示节点 6 的左右子树都已经遍历完成，直接输出 6。此时，可以将节点直接从栈中弹出 Pop()，之前用的只是 Peek()。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> path = new ArrayList<>();
        TreeNode lastVisit = root;
        TreeNode p = root;
        Stack<TreeNode> stack = new Stack<>();

        while (p != null || !stack.empty()) {
            while (p != null) {
                stack.push(p);
                p = p.left;
            }

            if (!stack.empty()) {
                TreeNode cur = stack.peek();
                if (lastVisit == cur.right || cur.right == null) {
                    stack.pop();
                    path.add(cur.val);
                    lastVisit = cur;
                } else {
                    p = cur.right;
                }
            }
        }
        return path;
    }
}

迭代写法 2

参考前序遍历的写法，前序遍历的顺序是 root -> left -> right，后序遍历的顺序是 left -> right -> root，把后序遍历序列 reverse 后，顺序为 root -> right -> left，其与前序遍历序列的区别在于前序遍历序列是先 left 后 right，而该序列是先 right 后 left。

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        LinkedList<TreeNode> stack = new LinkedList<>();
        LinkedList<Integer> ret = new LinkedList<>();

        if (root == null) return ret;

        stack.add(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pollLast();
            // 每次加到开头，或者和前序遍历序列一样加到结尾，然后最后的结果reverse
            ret.addFirst(node.val);
            // 遍历的顺序是先right后left，入栈的顺序相反
            if (node.left != null) stack.add(node.left);
            if (node.right != null) stack.add(node.right);
        }

        return ret;
    }
}

其他解法

https://leetcode-cn.com/problems/binary-tree-preorder-tra versal/solution/dai-ma-sui-xiang-lu-chi-tou-qian-zhong-hou-xu-de-d/
https://leetcode-cn.com/problems/binary-tree-preorder-traversal/solution/pythongai-bian-yi-xing-dai-ma-shi-xian-er-cha-shu-/

我们以中序遍历为例，之前说使用栈的话，无法同时解决处理过程和访问过程不一致的情况，那我们就将访问的节点放入栈中，把要处理的节点也放入栈中但是要做标记，标记就是要处理的节点放入栈之后，紧接着放入一个空指针作为标记。

中序

以树[1, 2, 3, 4, 5, 6] 为例:

初始root入栈: [1]
弹出 1 并入栈得到: [3, 1, null, 2]
弹出 2 并入栈得到: [3, 1, null, 5, 2, null, 4]
弹出 4 并入栈得到: [3, 1, null, 5, 2, null, 4, null]
弹出 null 并弹出 4 输出结果得到: [3, 1, null, 5, 2, null], ret = [4]
弹出 null 并弹出 2 输出结果得到: [3, 1, null, 5], ret = [4, 2]
弹出 5 并入栈得到: [3, 1, null, 5, null]
弹出 null 并弹出 5 输出结果得到: [3, 1, null], ret = [4, 2, 5]
弹出 null 并弹出 1 输出结果得到: [3], ret = [4, 2, 5, 1]
弹出 3 并入栈得到: [3, null, 6]
弹出 6 并入栈得到: [3, null, 6, null]
弹出 null 并弹出 6 输出结果: [3, null], ret = [4, 2, 5, 1, 6]
弹出 null 并弹出 3 输出结果: [], ret = [4, 2, 5, 1, 6, 3]

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        List<Integer> ret = new ArrayList<>();
        if (root != null) stack.push(root);

        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node != null) {
                if (node.right != null) stack.push(node.right);
				
                // 把root入栈并加入null标记下次该节点应该output
                stack.push(node);
                stack.push(null);

                if (node.left != null) stack.push(node.left);
            } else {
                node = stack.pop();
                ret.add(node.val);
            }
        }

        return ret;
    }
}

前序

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        List<Integer> ret = new ArrayList<>();

        if (root != null) stack.push(root);

        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node != null) {
                if (node.right != null) stack.push(node.right);
                if (node.left != null) stack.push(node.left);
                
                stack.push(node);
                stack.push(null);
            } else {
                node = stack.pop();
                ret.add(node.val);
            }
        }

        return ret;
    }
}

后序

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        List<Integer> ret = new ArrayList<>();

        if (root != null) stack.push(root);

        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node != null) {
                stack.push(node);
                stack.push(null);

                if (node.right != null) stack.push(node.right);
                if (node.left != null) stack.push(node.left);
            } else {
                node = stack.pop();
                ret.add(node.val);
            }
        }

        return ret;
    }
}

Reference

https://www.jianshu.com/p/456af5480cee
https://leetcode-cn.com/problems/binary-tree-postorder-traversal/solution/er-cha-shu-de-hou-xu-bian-li-by-leetcode/

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

[LeetCode][Tree] 94&144&145. Binary Tree InorderPreorderPostorder Traversal.md

[LeetCode][Tree] 94&144&145. Binary Tree InorderPreorderPostorder Traversal.md

144. Binary Tree Preorder Traversal [Medium]

迭代写法 1

迭代写法 2

94. Binary Tree Inorder Traversal [Medium]

迭代写法 1

145. Binary Tree Postorder Traversal [Hard]

迭代写法 1

迭代写法 2

其他解法

中序

前序

后序

Reference

Files

[LeetCode][Tree] 94&144&145. Binary Tree InorderPreorderPostorder Traversal.md

Latest commit

History

[LeetCode][Tree] 94&144&145. Binary Tree InorderPreorderPostorder Traversal.md

File metadata and controls

144. Binary Tree Preorder Traversal [Medium]

迭代写法 1

迭代写法 2

94. Binary Tree Inorder Traversal [Medium]

迭代写法 1

145. Binary Tree Postorder Traversal [Hard]

迭代写法 1

迭代写法 2

其他解法

中序

前序

后序

Reference