Skip to content

Latest commit

 

History

History
117 lines (99 loc) · 5 KB

[LeetCode][Tree] 236. Lowest Common Ancestor(LCA) of a Binary Tree.md

File metadata and controls

117 lines (99 loc) · 5 KB
Raw

Description

Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Given the following binary tree:  root = [3,5,1,6,2,0,8,null,null,7,4]   Example 1:

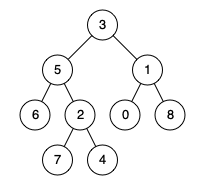
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.

  Note:

  • All of the nodes' values will be unique.
  • p and q are different and both values will exist in the binary tree.

Solution

遍历

从 root 开始遍历树，使用类似于前序遍历的方法，找到 p 、 q 节点，同时记录遍历的路径，得到公共祖先

 public class Solution {
     public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        List<TreeNode> path1 = new ArrayList<>();
        List<TreeNode> path2 = new ArrayList<>();
        findPath(root, p, new ArrayList<TreeNode>(), path1);
        findPath(root, q, new ArrayList<TreeNode>(), path2);

        TreeNode lca = root;
        int n = Math.min(path1.size(), path2.size());
        for (int i = 0; i < n; i++) {
            if (path1.get(i).val == path2.get(i).val) {
                lca = path1.get(i);
            } else {
                break;
            }
        }

        return lca;
    }
    
    /**
     * 找到从root到target的路径
     * 注意：这里一定需要curPath和path分别记录root到当前节点的路径和root到target的路径
     * 因为findPath并不会在找到target时结束递归调用，会继续递归，curPath会更新
     * 
     * @param cur
     * @param target
     * @param curPath 从root节点当当前节点的路径
     * @param path  找到target节点时的curPath值
     */
    private void findPath(TreeNode cur, TreeNode target, List<TreeNode> curPath, List<TreeNode> path) {
        if (cur == null) {
            return;
        }

        if (cur.val == target.val) {
            curPath.add(cur);
            path.addAll(curPath);
            return;
        }

        curPath.add(cur);
        findPath(cur.left, target, curPath, path);
        findPath(cur.right, target, curPath, path);
        curPath.remove(curPath.size() - 1);
    }
 }

Approach 1: Recursive Approach

上述的遍历方法在遍历过程中记录遍历经过的节点，backTrack函数并没有返回值，如果我们每层返回是否找到target节点的信息，就可以快速确定公共节点。

Example：

  1. p 、 q 分别是 LCA 左右子树。以题图中的树为例， p=6 , q=4 ， LCA = 5 。从 root 开始遍历，遍历到 6 时返回 true 表示找到了 p 节点，然后回到上层 5 时也返回 true 表示我找到了 p ，以此类推。同样，在遍历到 4 时也返回我找到了 q 的信息，一层层返回，直到返回到 5 节点， 5 现在直到了我的左子树找到了 p ，我的右子树找到了 q ，那我就是LCA。
  2. p 、 q 中一个是 LCA 。以题图中的树为例， p=5 , q=4 ，LCA = 5 。 5  3 会得到在左子树找到 p 的信息， 4 2 5 3 都会返回找到 q 的信息。因此 5 收到  q 找到的信息，同时判断自己就是 p ，可以确定该节点是 LCA 。
class Solution {
    private TreeNode ans;
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        recurseTree(root, p, q);
        return ans;
    }

    private boolean recurseTree(TreeNode curNode, TreeNode p, TreeNode q) {
        if (curNode == null) {
            return false;
        }

        int left = recurseTree(curNode.left, p, q) ? 1 : 0;
        int right = recurseTree(curNode.right, p, q) ? 1 : 0;
        int self = (curNode == p || curNode == q) ? 1 : 0;

        // 如果左子树，右子树，当前节点中有2个节点返回找到了p和q，就认为当前节点是LCA
        // 需要注意的是题目有限定每个节点是unique的，并且要找的节点一定存在，否则不能这样写
        if (left + right + self >= 2) {
            this.ans = curNode;
        }

        return (left + right + self > 0);
    }
}

Ref

https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree/solution/