[LeetCode][LinkedList][Divide And Conquer] 23. Merge k Sorted Lists.md

Description

Merge k sorted linked lists and return it as one sorted list. Analyze and describe its complexity. ** Example:

Input:
[
  1->4->5,
  1->3->4,
  2->6
]
Output: 1->1->2->3->4->4->5->6

Solution

Approach 5: Merge with Divide And Conquer

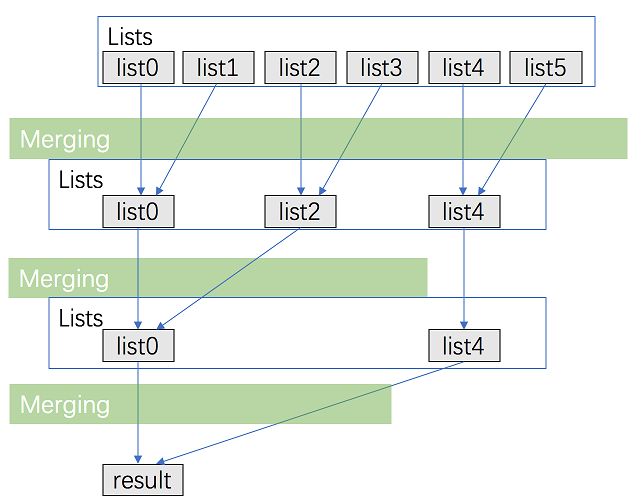
Intuition & Algorithm This approach walks alongside the one above but is improved a lot. We don't need to traverse most nodes many times repeatedly

• Pair up \text{k}k lists and merge each pair.

• After the first pairing, \text{k}k lists are merged into k/2_k_/2 lists with average 2N/k2_N_/k length, then k/4_k_/4, k/8_k_/8 and so on.

• Repeat this procedure until we get the final sorted linked list.

Thus, we'll traverse almost N_N_ nodes per pairing and merging, and repeat this procedure about \log_{2}{k}log2_k_ times.

Example: 加入有10个list需要合并，编号分别为 0 - 9，每次merge的分别为：

0 - 1 2 - 3 4 - 5 6 - 7 8 - 9

0 - 2 4 - 6

0 - 4

0 - 8

public class Solution {
    // Definition for singly-linked list.
    public class ListNode {
        int val;
        ListNode next;

        ListNode(int x) {
            val = x;
        }
    }

    public ListNode mergeKLists(ListNode[] lists) {
        int interval = 1;
        int n = lists.length;
        while (interval < n) {
            int steps = interval * 2;
            for (int i = 0; i < n - interval; i += steps) {
                lists[i] = mergeTwoLists(lists[i], lists[i + interval]);
            }
            interval *= 2;
        }
        return n > 0 ? lists[0] : null;
    }

    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(0);
        ListNode cur = dummy;

        ListNode p1 = l1, p2 = l2;
        while (p1 != null && p2 != null) {
            if (p1.val < p2.val) {
                cur.next = p1;
                p1 = p1.next;
            } else {
                cur.next = p2;
                p2 = p2.next;
            }
            cur = cur.next;
        }

        cur.next = p1 == null ? p2 : p1;

        return dummy.next;
    }
}