4_二叉树.md

二叉树

一、二叉树的递归结构

*1、二叉树的最大深度（104）

104. 二叉树的最大深度

public int maxDepth(TreeNode root) {
  if(root==null){
    return 0;
  }
  return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
}

@Test
public void test(){
  int[] pre ={3,9,20,15,7};
  int[] in ={9,3,15,20,7};
  /**
          3
         / \
         9  20
         /  \
         15   7
         */
  TreeNode root= TreeNodeUtils.ConstructBinaryTree(pre,in);
  System.out.println(maxDepth(root));
}

*2、二叉树的最小深度（111）

111. 二叉树的最小深度

//TODO:最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
public int minDepth(TreeNode root) {
  if(root==null){
    return 0;
  }

  /**
         * 针对
         *     1
         *     \
         *      2
         *  的情况
         */
  if(root.left==null){
    return minDepth(root.right)+1;
  }

  /**
         * 针对
         *      1
         *     /
         *    2
         * 的情况
         */
  if(root.right==null){
    return minDepth(root.left)+1;
  }

  return Math.min(minDepth(root.left),minDepth(root.right))+1;
}

@Test
public void test(){
  int[] pre ={3,9,20,15,7};
  int[] in ={9,3,15,20,7};
  /**
         3
         / \
         9  20
         /  \
         15   7
         */
  TreeNode root= TreeNodeUtils.ConstructBinaryTree(pre,in);
  System.out.println(minDepth(root));
}

*3、翻转二叉树（226)

226. 翻转二叉树

public TreeNode invertTree(TreeNode root) {
  if(root == null){
    return root;
  }

  TreeNode newRoot = new TreeNode(root.val);

  newRoot.right = invertTree(root.left);
  newRoot.left = invertTree(root.right);
  return newRoot;
}

@Test
public void test(){
  int[] pre={4,2,1,3,7,6,9};
  int[] in={1,2,3,4,6,7,9};
  TreeNode root= TreeNodeUtils.ConstructBinaryTree(pre,in);

  List<List<Integer>> res = TreeNodeUtils.levelOrder(root);
  for(List<Integer> list : res){
    System.out.println(list);
  }
  System.out.println("=============");

  root = invertTree(root);
  List<List<Integer>> res2 = TreeNodeUtils.levelOrder(root);
  for(List<Integer> list : res2){
    System.out.println(list);
  }
}

4、相同的树（100）

100. 相同的树

public boolean isSameTree(TreeNode p, TreeNode q) {
  if(p ==null && q==null){
    return true;
  }
  if(p ==null || q==null){
    //p或者q有一个是 null,不存在 p、q 都是 null 的情况
    return false;
  }
  if(p.val != q.val){
    return false;
  }

  return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}

@Test
public void test(){
  //        int[] pre1={1,2,3};
  //        int[] in1={2,1,3};
  //        TreeNode p = TreeNodeUtils.ConstructBinaryTree(pre1,in1);
  //
  //        int[] pre2={1,2,3};
  //        int[] in2={2,1,3};
  //        TreeNode q = TreeNodeUtils.ConstructBinaryTree(pre2,in2);

  int[] pre1={1,2,1};
  int[] in1={2,1,1};
  TreeNode p = TreeNodeUtils.ConstructBinaryTree(pre1,in1);

  int[] pre2={1,1,2};
  int[] in2={1,1,2};
  TreeNode q = TreeNodeUtils.ConstructBinaryTree(pre2,in2);

  System.out.println(isSameTree(p,q));
}

5、对称二叉树(101)

101. 对称二叉树

public boolean isSymmetric(TreeNode root) {
  if(root==null){
    return true;
  }
  return isSymmetric(root.left,root.right);
}

//判断 p q 是否对称
private boolean isSymmetric(TreeNode p,TreeNode q) {
  if(p==null && q==null){
    return true;
  }
  if(p==null || q==null){
    return false;
  }
  if(p.val != q.val){
    return false;
  }
  return isSymmetric(p.left,q.right) &&
    isSymmetric(p.right,q.left);
}

@Test
public void test(){
  //int[] pre={1,2,3,4,2,4,3};
  //int[] in={3,2,4,1,4,2,3};
  int[] pre={1,2,3,2,3};
  int[] in={2,3,1,2,3};
  TreeNode root = TreeNodeUtils.ConstructBinaryTree(pre,in);
  System.out.println(isSymmetric(root));
}

6、合并二叉树（617）

617. 合并二叉树

public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
    if(t1==null){
        return t2;
    }
    if(t2==null){
        return t1;
    }

    TreeNode root = new TreeNode(t1.val+t2.val);
    root.left = mergeTrees(t1.left,t2.left);
    root.right = mergeTrees(t1.right,t2.right);
    return root;
}

@Test
public void test(){
    int[] pre1={1,3,5,2};
    int[] in1={5,3,1,2};
    TreeNode t1 = TreeNodeUtils.ConstructBinaryTree(pre1,in1);

    int[] pre2={2,1,4,3,7};
    int[] in2={1,4,2,3,7};
    TreeNode t2= TreeNodeUtils.ConstructBinaryTree(pre2,in2);

    TreeNode t = mergeTrees(t1,t2);
    System.out.println(TreeNodeUtils.levelOrder(t));
}

7、二叉树的最近公共祖先（236）

236. 二叉树的最近公共祖先

//思路一:
//分三种情况讨论
//1、p、q 都在左子树
//2、p、q 都在右子树
//3、p、q 分别在左子树、右子树或者在右子树、左子树中。
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if(root==null){
        return null;
    }
    // p ,q 都在左子树
    if(contains(root.left,p) && contains(root.left,q)){
        return lowestCommonAncestor(root.left,p,q);
    }
    // p，q 都在右子树
    if(contains(root.right,p) && contains(root.right,q)){
        return lowestCommonAncestor(root.right,p,q);
    }
    return root;
}

//判断已 root 为根节点二叉树是否包含 p 节点
private boolean contains(TreeNode root,TreeNode p){
    if(root==null || p==null){
        return false;
    }
    if(root.val == p.val){
        return true;
    }
    return contains(root.left,p) || contains(root.right,p);
}

@Test
public void test(){
    int[] pre = {3,5,6,2,7,4,1,0,8};
    int[] in = {6,5,7,2,4,3,0,1,8};
    TreeNode root = TreeNodeUtils.ConstructBinaryTree(pre,in);
    TreeNode p = new TreeNode(5);
    //TreeNode q = new TreeNode(1);
    TreeNode q = new TreeNode(4);
    System.out.println(lowestCommonAncestor(root,p,q).val);
}

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if(root == null){
        return null;
    }
    //如果 p或者是q是根节点，那么该root就是他们最近的公共父节点
    if(p== root || q==root){
        return root;
    }
    //p，q 在左子树中是否有公共父节点
    TreeNode left = lowestCommonAncestor(root.left,p,q);
    //p，q 在右子树中是否有公共父节点
    TreeNode right = lowestCommonAncestor(root.right,p,q);
    if(left!=null && right!=null){
        return root;
    }
    if(left != null){
        return left;
    }
    if(right != null){
        return right;
    }
    return null;
}

@Test
public void test2(){
    int[] pre = {3,5,6,2,7,4,1,0,8};
    int[] in = {6,5,7,2,4,3,0,1,8};
    TreeNode root = TreeNodeUtils.ConstructBinaryTree(pre,in);
    TreeNode p = root.left;
    TreeNode q = root.right;
    //TreeNode q = root.left.right.right;
    System.out.println(lowestCommonAncestor(root,p,q).val);
}

二、二叉树的路径问题

*1、二叉树的所有路径（257）

257. 二叉树的所有路径

//思路：
//递归思想：将一棵树拆成 root->左子树对应字符串 + root->右子树对应的字符串

//在左子树进行相同的操作：

//在右子树进行相同的操作：

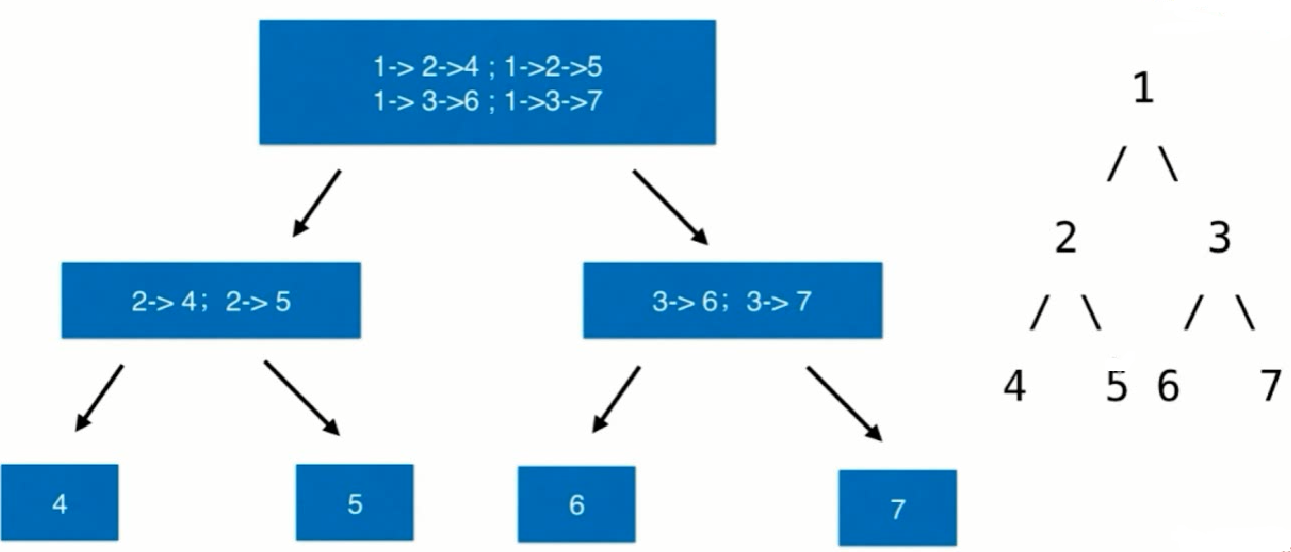
public List<String> binaryTreePaths(TreeNode root) {
    List<String> res = new ArrayList<>();
    if(root==null){
        return res;
    }
    if(root.left==null && root.right==null){ //如果 root 是叶子节点
        res.add(root.val+"");
        return res;
    }

    List<String> leftS = binaryTreePaths(root.left);
    for(String s : leftS){
        res.add(root.val+"->"+s);
    }
    List<String> rightS = binaryTreePaths(root.right);
    for(String s : rightS){
        res.add(root.val+"->"+s);
    }
    return res;
}

@Test
public void test(){
    //int[] pre = {1,2,5,3};
    //int[] in={2,5,1,3};
    int[] pre={1,2,4,5,3,6,7};
    int[] in={4,2,5,1,6,3,7};
    TreeNode root = TreeNodeUtils.ConstructBinaryTree(pre,in);
    System.out.println(binaryTreePaths(root));
}

//思路二：
//回溯法
public List<String> binaryTreePaths(TreeNode root) {
    List<String> paths = new ArrayList<>();
    if(root==null){
        return paths;
    }
    List<Integer> vlaues = new ArrayList<>();
    backtrack(root,vlaues,paths);
    return paths;
}

// values : 记录从根节点到叶子节点的所有路径
// paths : 存储所有可能的结果
private void backtrack(TreeNode root,List<Integer> values,List<String> paths){
    if(root==null){
        return;
    }
    values.add(root.val);
    if(root.left==null && root.right==null){
        paths.add(buildPath(values));
    }else{
        backtrack(root.left,values,paths);
        backtrack(root.right,values,paths);
    }
    values.remove(values.size()-1);
}

//根据 values 去构建路径
private String buildPath(List<Integer> values){
    StringBuilder builder = new StringBuilder();
    for(int i=0;i<values.size();i++){
        if(i==values.size()-1){
            builder.append(values.get(i));
        }else{
            builder.append(values.get(i)+"->");
        }
    }
    return builder.toString();
}

@Test
public void test(){
    //int[] pre = {1,2,5,3};
    //int[] in={2,5,1,3};
    int[] pre={1,2,4,5,3,6,7};
    int[] in={4,2,5,1,6,3,7};
    TreeNode root = TreeNodeUtils.ConstructBinaryTree(pre,in);
    System.out.println(binaryTreePaths(root));
}

2、路径总和（112）

112. 路径总和

public boolean hasPathSum(TreeNode root, int sum) {
    if(root==null){
        return false;
    }
    if((root.left==null && root.right==null) && (root.val==sum) ){
        return true;
    }
    return hasPathSum(root.left,sum-root.val) ||
        hasPathSum(root.right,sum-root.val);
}

@Test
public void test(){
    int[] pre={5,4,11,7,2,8,13,4,1};
    int[] in={7,11,2,4,5,13,8,4,1};
    TreeNode root = TreeNodeUtils.ConstructBinaryTree(pre,in);
    int sum=22;
    System.out.println(hasPathSum(root,sum));
}

3、路径总和 II（113）

113. 路径总和 II

//思路：
//首要的任务就是获取从根节点到叶子结点的路径。
//思路与 257 的使用回溯法相同
public List<List<Integer>> pathSum(TreeNode root, int sum) {
    //记录从根节点到叶子节点的一条满足条件的路径
    List<Integer> values = new ArrayList<>();
    List<List<Integer>> paths = new ArrayList<>();
    backtrack(root,values,paths,sum);
    return paths;
}

//使用回溯法获取从根节点到叶子节点的路径
private void backtrack(TreeNode root,List<Integer> values,List<List<Integer>> paths,int sum){
    if(root==null){
        return;
    }
    values.add(root.val);
    if((root.left==null && root.right==null) && sum==root.val){
        //注意 add() 集合的方式
        paths.add(new ArrayList<>(values));
    }else{
        backtrack(root.left,values,paths,sum-root.val);
        backtrack(root.right,values,paths,sum-root.val);
    }
    values.remove(values.size()-1);
}

@Test
public void test(){
    int[] pre={5,4,11,7,2,8,13,4,5,1};
    int[] in={7,11,2,4,5,13,8,5,4,1};
    int sum =22;
    TreeNode root = TreeNodeUtils.ConstructBinaryTree(pre,in);
    System.out.println(pathSum(root,sum));
}

**4、路径总和 III（437）

437. 路径总和 III

//以root为根节点的二叉树中，寻找和为sum的路径，返回这样的路径的个数
public int pathSum(TreeNode root, int sum) {
    if(root==null){
        return 0;
    }
    int res = findPath(root,sum);
    res += pathSum(root.left,sum);
    res += pathSum(root.right,sum);
    return res;
}

//以node为根节点的二叉树中，寻找包含node的路径，和为sum
private int findPath(TreeNode node,int sum){
    if(node==null){
        return 0;
    }
    int res =0;
    if(node.val==sum){ //说明包含 node 节点
        res +=1;
    }
    res += findPath(node.left,sum-node.val);
    res += findPath(node.right,sum-node.val);
    return res;
}

@Test
public void test(){
    int[] pre={1,2,6,3,4};
    int[] in={6,2,1,4,3};
    TreeNode root = TreeNodeUtils.ConstructBinaryTree(pre,in);
    int sum =7;
    System.out.println(pathSum(root,sum));
}

5、左叶子之和（404）

404. 左叶子之和

public int sumOfLeftLeaves(TreeNode root) {
    if(root==null){
        return 0;
    }

    int sum=0;

    //判断 root.left 是否是左叶子
    if(root.left!=null && 
       (root.left.left==null && root.left.right==null)){
        sum += root.left.val; // root.left 就是则叶子
    }
    sum += sumOfLeftLeaves(root.left) + sumOfLeftLeaves(root.right);
    return sum;
}

@Test
public void test(){
    int[] pre={3,9,20,15,7};
    int[] in={9,3,15,20,7};
    TreeNode root = TreeNodeUtils.ConstructBinaryTree(pre,in);
    System.out.println(sumOfLeftLeaves(root));
}

6、求根到叶子节点数字之和（129）

129. 求根到叶子节点数字之和

//思路一：
//回溯法
private int sum=0;

public int sumNumbers(TreeNode root) {
    List<Integer> values = new ArrayList<>();
    backtrack(root,values);
    return sum;
}

private void backtrack(TreeNode root, List<Integer> values){
    if(root==null){
        return;
    }
    values.add(root.val);
    if(root.left==null && root.right==null){
        int num = 0;
        for(int i=values.size()-1;i>=0;i--){
            num += values.get(i)*Math.pow((double)10,(values.size()-1)-i);
        }
        sum += num;
    }else{
        backtrack(root.left,values);
        backtrack(root.right,values);
    }
    values.remove(values.size()-1);
}

@Test
public void test(){
    int[] pre={4,9,5,1,0};
    int[] in={5,9,1,4,0};
    TreeNode root = TreeNodeUtils.ConstructBinaryTree(pre,in);
    System.out.println(sumNumbers(root));
}

//思路二：
//深度遍历
public int sumNumbers(TreeNode root) {
    if(root==null){
        return 0;
    }
    return dfs(root,0);
}

// sum 记录的是从根节点到叶子节点的数值和
// sum 的初始值为 0
private int dfs(TreeNode root,int sum){
    if(root==null){
        return 0;
    }
    if(root.left==null && root.right==null){
        return sum*10+root.val; // sum 初始值为0，root 是叶子节点，则返回值就是 root.val
    }
    return dfs(root.left,sum*10+root.val)+
        dfs(root.right,sum*10+root.val);
}

@Test
public void test(){
    int[] pre={4,9,5,1,0};
    int[] in={5,9,1,4,0};
    TreeNode root = TreeNodeUtils.ConstructBinaryTree(pre,in);
    System.out.println(sumNumbers(root));
}

三、完全二叉树

1、判断一棵树是否是完全二叉树

//思路：
//任意的一个二叉树，都可以补成一个满二叉树。这样中间就会有很多空洞。
//在广度优先遍历的时候，如果是满二叉树，
//或者完全二叉树，这些空洞是在广度优先的遍历的末尾，
//所以，但我们遍历到空洞的时候，整个二叉树就已经遍历完成了。
//如果是非完全二叉树，
//我们遍历到空洞的时候，就会发现，空洞后面还有没有遍历到的值。
//这样，只要根据是否遍历到空洞，整个树的遍历是否结束来判断是否是完全的二叉树。
public boolean isCompeteTree(TreeNode root){
    if (root==null)
        return true;

    Queue<TreeNode> queue=new LinkedList<>();
    queue.add(root);
    //将该二叉树填满为满二叉树，不满的位置使用 null 保持
    while(true){
        TreeNode node = queue.poll();
        if(node==null){
            break;
        }
        queue.add(node.left);
        queue.add(node.right);
    }
    while (!queue.isEmpty()){
        TreeNode t=queue.poll();
        if (t!=null){
            return false;
        }
    }
    return true;
}

@Test
public void test(){
    int[] pre={1,2,4,5,3};
    int[] in={4,2,5,1,3};
    //        int[] pre ={1,2,4,5};
    //        int[] in={4,2,5,1};
    TreeNode root=TreeNodeUtils.ConstructBinaryTree(pre,in);
    System.out.println(isCompeteTree(root));
}

2、完全二叉树的节点个数(222)

222. 完全二叉树的节点个数

//写法一：使用递归结构处理
//存在问题：时间复杂度过高
public int countNodes(TreeNode root) {
  if(root==null){
    return 0;
  }
  if(root.left==null && root.right==null){
    return 1;
  }
  return countNodes(root.left)+countNodes(root.right)+1;
}

@Test
public void test(){
  /**
             1
            / \
           2   3
          / \  /
         4  5 6
         */
  //int[] pre={1,2,4,5,3,6};
  //int[] in={4,2,5,1,6,3};
  /**
               1
             /  \
            2    3
           / \  / \
          4  5 6  7
         */
  int[] pre={1,2,4,5,3,6,7};
  int[] in={4,2,5,1,6,3,7};
  TreeNode root= TreeNodeUtils.ConstructBinaryTree(pre,in);
  System.out.println(countNodes(root));
}

//写法二：
//改进：
//1、满二叉树是一种特殊的完全的二叉树，利用满二叉树是性质对统计进行改进
//2、以某一个节点为根节点的子树是满二叉树，则该满二叉树的节点数数为(2^h - 1),
// h 为该满二叉树的高度
public int countNodes(TreeNode root) {
  if(root==null){
    return 0;
  }

  int l = getLeftHeight(root);
  int r = getRightHeight(root);
  if(l==r){ //满二叉树
    return (2<<l)-1; //二叉树的节点数数为(2^h - 1),h 就是该满二叉树的高度
  }else{
    return countNodes(root.left)+countNodes(root.right)+1;
  }
}

// 获取以 root 为根节点的
// TODO:左子树高度
private int getLeftHeight(TreeNode root){
  if(root==null){
    return 0;
  }
  int h=0;
  while(root.left!=null){
    h++;
    root=root.left;
  }
  return h;
}

// 获取以 root 为根节点的
// TODO:右子树高度
private int getRightHeight(TreeNode root){
  if(root==null){
    return 0;
  }
  int h=0;
  while(root.right!=null){
    h++;
    root=root.right;
  }
  return h;
}

@Test
public void test(){
  /**
             1
            / \
           2   3
          / \  /
         4  5 6
         */
  //int[] pre={1,2,4,5,3,6};
  //int[] in={4,2,5,1,6,3};
  /**
               1
             /  \
            2    3
           / \  / \
          4  5 6  7
         */
  int[] pre={1,2,4,5,3,6,7};
  int[] in={4,2,5,1,6,3,7};
  TreeNode root= TreeNodeUtils.ConstructBinaryTree(pre,in);
  System.out.println(countNodes(root));
}

四、二叉搜索树

*1、二叉搜索树的最近公共祖先（235）

235.二叉搜索树的最近公共祖先

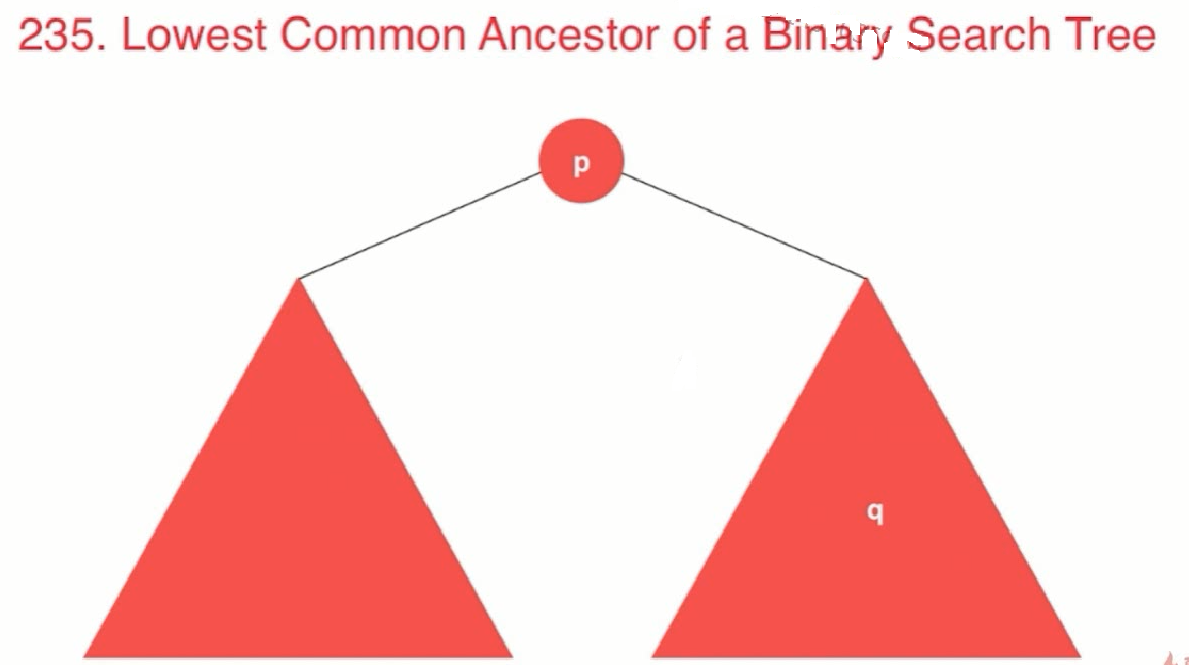
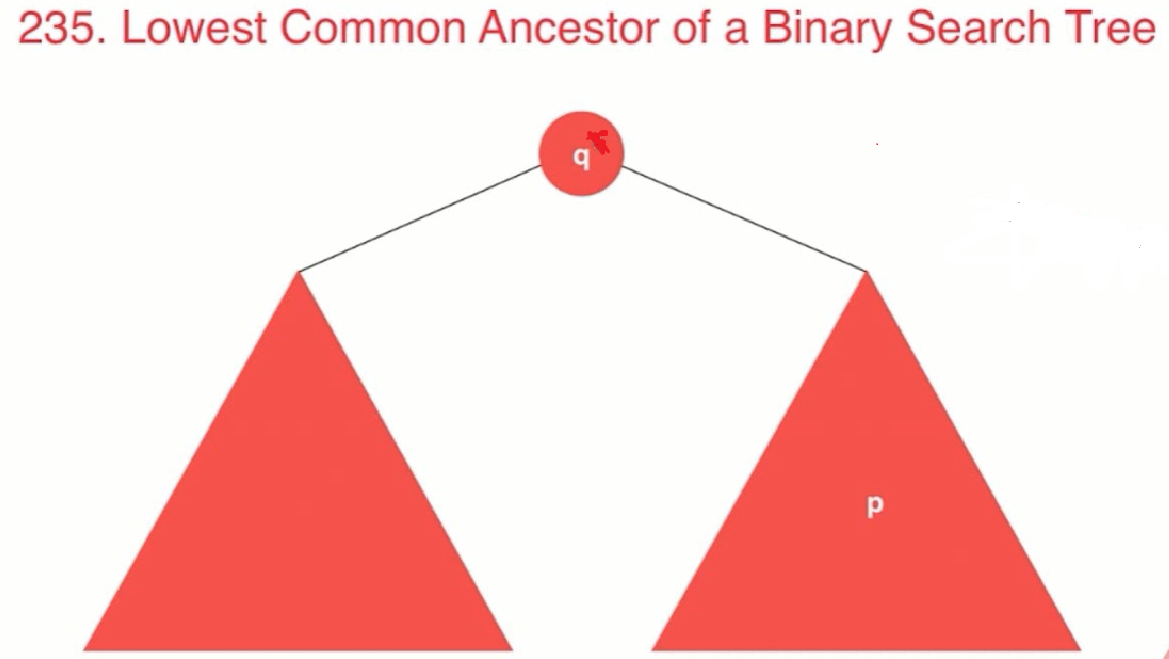
//思路：利用二叉搜索树的性质
//p,q 都是该二分搜索树的节点，对于p,q节点的公共祖先节点，分为3个情况：
//(1) p，q值都小于node，则他们的公共祖先在node的左子树中

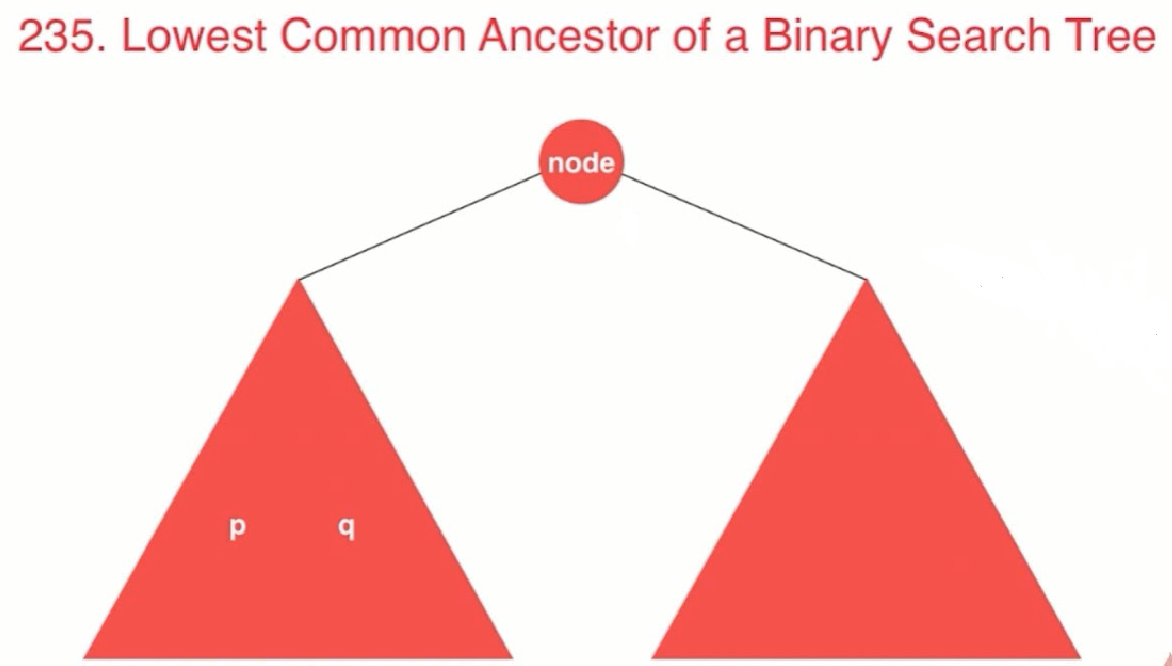
//(2) p，q值都大于node，则他们的公共祖先在node的右子树中

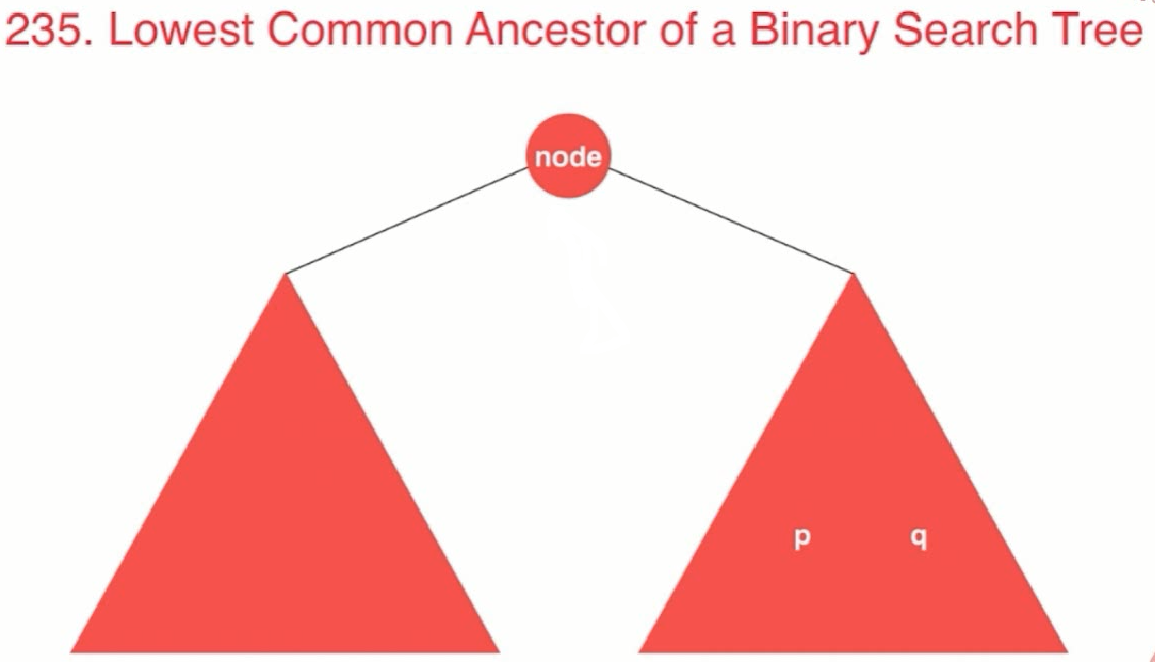
//(3) node在p,q之间的，则他们的公共祖先就是node

2、二叉搜索树结点最小距离（783）

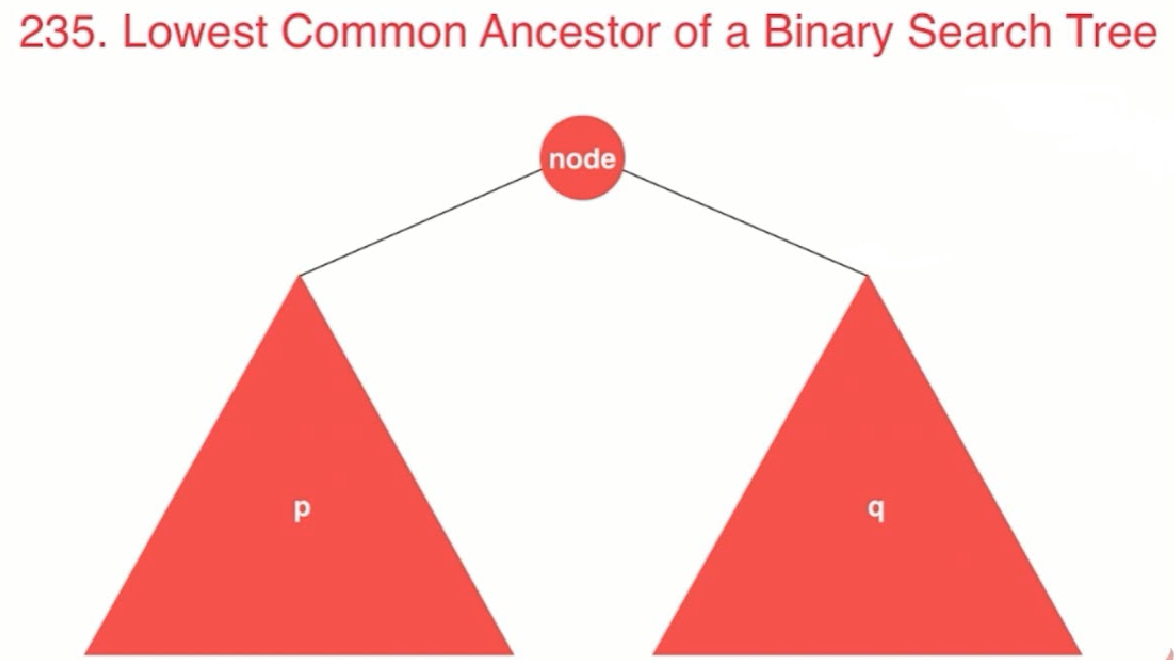
783. 二叉搜索树结点最小距离

//思路：
//利用 BST 中序遍历性质
//实际上就是计算相邻元素的最小值
public int minDiffInBST(TreeNode root) {
    inOrder(root);

    int min = Integer.MAX_VALUE;
    for(int i=1;i<list.size();i++){
        min = Math.min(min,list.get(i)-list.get(i-1));
    }
    return min;
}

private List<Integer> list = new ArrayList<>();

private void inOrder(TreeNode root){
    if(root==null){
        return;
    }
    inOrder(root.left);
    list.add(root.val);
    inOrder(root.right);
}

@Test
public void test(){
    int[] pre={4,2,1,3,6};
    int[] in={1,2,3,4,6};
    TreeNode root = TreeNodeUtils.ConstructBinaryTree(pre,in);
    System.out.println(minDiffInBST(root));
}

*3、 验证二叉搜索树（98）

98. 验证二叉搜索树

//思路：
//在 BST 中，存在
//左子树的最大值 < 根节点 < 右子树的最最小值
//而且这个是递归存在的
//这样，就可以精确形如
//   2
//  / \
// 1   3
//的 BST
public boolean isValidBST(TreeNode root) {
    return isValid(root,Long.MIN_VALUE, Long.MAX_VALUE);
}

// leftMax 是以 root 为根结点的 BST 的左子树的最大值
// rightMax 是以 root 为根据节点的 BST 的右子树的最小值
private boolean isValid(TreeNode root,long leftMax,long rightMin){
    if(root==null){
        return true;
    }
    if(root.left == null && root.right==null){
        if(leftMax < root.val && rightMin > root.val){
            return true;
        }
    }
    if(root.val <= leftMax || root.val >= rightMin){
        //不满足 BST 的性质
        return false;
    }
    return isValid(root.left,leftMax,root.val) &&
        isValid(root.right,root.val,rightMin);
}

@Test
public void test(){
    int[] pre = {2,1,3};
    int[] in={1,2,3};
    //int[] pre={5,1,4,3,6};
    //int[] in={1,5,3,4,6};
    TreeNode root = TreeNodeUtils.ConstructBinaryTree(pre,in);
    System.out.println(isValidBST(root));
}

*4、删除二叉搜索树中的节点（450）

450. 删除二叉搜索树中的节点

public TreeNode deleteNode(TreeNode root, int key) {
    if(root==null){
        return null;
    }
    if(root.val==key){ // root 是要删除的顶点
        //先判断 root 的右子树是否为空
        if(root.right==null){
            root = root.left;//直接删除根节点，注意实际上是这里删除了节点
            return root;
        }else{ //说明存在右子树，将右子树的最小值与 根节点值进行交换
            //获取右子树的最小值
            TreeNode rightTree = root.right;
            while(rightTree.left!=null){
                rightTree = rightTree.left;
            }
            //注意这里是交换数据，而不是更新数据
            int tmp = rightTree.val;
            rightTree.val = root.val;
            root.val = tmp;
        }
    }
    root.left = deleteNode(root.left,key);
    root.right = deleteNode(root.right,key);
    return root;
}

@Test
public void test(){
    int[] pre={5,3,2,4,6,7};
    int[] in={2,3,4,5,6,7};
    TreeNode root = TreeNodeUtils.ConstructBinaryTree(pre,in);
    System.out.println(TreeNodeUtils.levelOrder(root));
    int key=3;
    root = deleteNode(root,key);
    System.out.println(TreeNodeUtils.levelOrder(root));
}

5、二分搜索树搜索

//根据 key 查找相应的节点
//时间复杂度是 O(h)
private TreeNode findNode(TreeNode root,int key){
    if(root==null){
        return null;
    }
    if(root.val == key){
        return root;
    }else if(root.val<key){ // 在右子树中查找
        return findNode(root.right,key);
    }else{
        assert root.val > key;
        return findNode(root.left,key);
    }
}

*6、将有序数组转换为二叉搜索树（108）

108. 将有序数组转换为二叉搜索树

public TreeNode sortedArrayToBST(int[] nums) {
    if(nums==null || nums.length==0){
        return null;
    }
    return buildTree(nums,0, nums.length-1);
}

//[start,end] 范围内创建二叉树
private TreeNode buildTree(int[] nums,int start,int end){
    if(start>end){
        return null;
    }
    if(start == end){
        return new TreeNode(nums[start]);
    }
    int mid = (end - start)/2 + start;
    TreeNode root = new TreeNode(nums[mid]);
    root.left = buildTree(nums,start,mid-1);
    root.right = buildTree(nums,mid+1,end);
    return root;
}

@Test
public void test(){
    int[] nums={-10,-3,0,5,9};
    TreeNode root=sortedArrayToBST(nums);
    System.out.println(TreeNodeUtils.inorderTraversal(root));
    System.out.println(TreeNodeUtils.postorderTraversal(root));
}

7、二叉搜索树中第K小的元素（230）

230. 二叉搜索树中第K小的元素

public int kthSmallest(TreeNode root, int k) {
    inOrder(root,k);
    return res;
}

int m= 0 ;
int res = 0;

private void inOrder(TreeNode root,int k){
    if(root==null){
        return;
    }
    inOrder(root.left,k);
    m++;
    if(m==k){
        res = root.val;
    }
    inOrder(root.right,k);
}

@Test
public void test(){
    //int[] pre={5,3,2,1,4,6};
    //int[] in={1,2,3,4,5,6};
    //int k=3;

    int[] pre={3,1,2,4};
    int[] in={1,2,3,4};
    int k=1;
    TreeNode root = TreeNodeUtils.ConstructBinaryTree(pre,in);
    System.out.println(kthSmallest(root,k));
}