-
Notifications
You must be signed in to change notification settings - Fork 1.1k
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
- Loading branch information
Showing
7 changed files
with
233 additions
and
6 deletions.
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,171 @@ | ||
| # [1584. 连接所有点的最小费用](https://leetcode.cn/problems/min-cost-to-connect-all-points/) | ||
|
|
||
| - 标签:并查集、图、数组、最小生成树 | ||
| - 难度:中等 | ||
|
|
||
| ## 题目链接 | ||
|
|
||
| - [1584. 连接所有点的最小费用 - 力扣](https://leetcode.cn/problems/min-cost-to-connect-all-points/) | ||
|
|
||
| ## 题目大意 | ||
|
|
||
| **描述**:给定一个 $points$ 数组,表示 2D 平面上的一些点,其中 $points[i] = [x_i, y_i]$。 | ||
|
|
||
| 链接点 $[x_i, y_i]$ 和点 $[x_j, y_j]$ 的费用为它们之间的 **曼哈顿距离**:$|x_i - x_j| + |y_i - y_j|$。其中 $|val|$ 表示 $val$ 的绝对值。 | ||
|
|
||
| **要求**:返回将所有点连接的最小总费用。 | ||
|
|
||
| **说明**: | ||
|
|
||
| - 只有任意两点之间有且仅有一条简单路径时,才认为所有点都已连接。 | ||
| - $1 \le points.length \le 1000$。 | ||
| - $-10^6 \le x_i, y_i \le 10^6$。 | ||
| - 所有点 $(x_i, y_i)$ 两两不同。 | ||
|
|
||
| **示例**: | ||
|
|
||
| - 示例 1: | ||
|
|
||
| 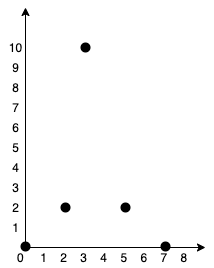 | ||
|
|
||
|  | ||
|
|
||
| ```python | ||
| 输入:points = [[0,0],[2,2],[3,10],[5,2],[7,0]] | ||
| 输出:20 | ||
| 解释:我们可以按照上图所示连接所有点得到最小总费用,总费用为 20 。 | ||
| 注意到任意两个点之间只有唯一一条路径互相到达。 | ||
| ``` | ||
|
|
||
| - 示例 2: | ||
|
|
||
| ```python | ||
| 输入:points = [[3,12],[-2,5],[-4,1]] | ||
| 输出:18 | ||
| ``` | ||
|
|
||
| ## 解题思路 | ||
|
|
||
| 将所有点之间的费用看作是边,则所有点和边可以看作是一个无向图。每两个点之间都存在一条无向边,边的权重为两个点之间的曼哈顿距离。将所有点连接的最小总费用,其实就是求无向图的最小生成树。对此我们可以使用 Prim 算法或者 Kruskal 算法。 | ||
|
|
||
| ### 思路 1:Prim 算法 | ||
|
|
||
| 每次选择最短边来扩展最小生成树,从而保证生成树的总权重最小。算法通过不断扩展小生成树的顶点集合 $MST$,逐步构建出最小生成树。 | ||
|
|
||
| ### 思路 1:代码 | ||
|
|
||
| ```Python | ||
| class Solution: | ||
| def distance(self, point1, point2): | ||
| return abs(point1[0] - point2[0]) + abs(point1[1] - point2[1]) | ||
|
|
||
| def Prim(self, points, start): | ||
| size = len(points) | ||
| vis = set() | ||
| dis = [float('inf') for _ in range(size)] | ||
|
|
||
| ans = 0 # 最小生成树的边权值 | ||
| dis[start] = 0 # 起始位置到起始位置的边权值初始化为 0 | ||
|
|
||
| for i in range(1, size): | ||
| dis[i] = self.distance(points[start], points[i]) | ||
| vis.add(start) | ||
|
|
||
| for _ in range(size - 1): # 进行 n 轮迭代 | ||
| min_dis = float('inf') | ||
| min_dis_i = -1 | ||
| for i in range(size): | ||
| if i not in vis and dis[i] < min_dis: | ||
| min_dis = dis[i] | ||
| min_dis_i = i | ||
| if min_dis_i == -1: | ||
| return -1 | ||
|
|
||
| ans += min_dis | ||
| vis.add(min_dis_i) | ||
|
|
||
|
|
||
| for i in range(size): | ||
| if i not in vis: | ||
| dis[i] = min(dis[i], self.distance(points[i], points[min_dis_i])) | ||
|
|
||
| return ans | ||
|
|
||
| def minCostConnectPoints(self, points: List[List[int]]) -> int: | ||
| return self.Prim(points, 0) | ||
| ``` | ||
|
|
||
| ### 思路 1:复杂度分析 | ||
|
|
||
| - **时间复杂度**:$O(n^2)$。 | ||
| - **空间复杂度**:$O(n^2)$。 | ||
|
|
||
| ### 思路 2:Kruskal 算法 | ||
|
|
||
| 通过依次选择权重最小的边并判断其两个端点是否连接在同一集合中,从而逐步构建最小生成树。这个过程保证了最终生成的树是无环的,并且总权重最小。 | ||
|
|
||
| ### 思路 2:代码 | ||
|
|
||
| ```python | ||
| class UnionFind: | ||
|
|
||
| def __init__(self, n): | ||
| self.parent = [i for i in range(n)] | ||
| self.count = n | ||
|
|
||
| def find(self, x): | ||
| while x != self.parent[x]: | ||
| self.parent[x] = self.parent[self.parent[x]] | ||
| x = self.parent[x] | ||
| return x | ||
|
|
||
| def union(self, x, y): | ||
| root_x = self.find(x) | ||
| root_y = self.find(y) | ||
| if root_x == root_y: | ||
| return | ||
|
|
||
| self.parent[root_x] = root_y | ||
| self.count -= 1 | ||
|
|
||
| def is_connected(self, x, y): | ||
| return self.find(x) == self.find(y) | ||
|
|
||
|
|
||
| class Solution: | ||
| def Kruskal(self, edges, size): | ||
| union_find = UnionFind(size) | ||
|
|
||
| edges.sort(key=lambda x: x[2]) | ||
|
|
||
| ans, cnt = 0, 0 | ||
| for x, y, dist in edges: | ||
| if union_find.is_connected(x, y): | ||
| continue | ||
| ans += dist | ||
| cnt += 1 | ||
| union_find.union(x, y) | ||
| if cnt == size - 1: | ||
| return ans | ||
| return ans | ||
|
|
||
| def minCostConnectPoints(self, points: List[List[int]]) -> int: | ||
| size = len(points) | ||
| edges = [] | ||
| for i in range(size): | ||
| xi, yi = points[i] | ||
| for j in range(i + 1, size): | ||
| xj, yj = points[j] | ||
| dist = abs(xi - xj) + abs(yi - yj) | ||
| edges.append([i, j, dist]) | ||
|
|
||
| ans = self.Kruskal(edges, size) | ||
| return ans | ||
|
|
||
| ``` | ||
|
|
||
| ### 思路 2:复杂度分析 | ||
|
|
||
| - **时间复杂度**:$O(m \times \log(n))$。其中 $m$ 为边数,$n$ 为节点数,本题中 $m = n^2$。 | ||
| - **空间复杂度**:$O(n^2)$。 | ||
|
|
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,55 @@ | ||
| class UnionFind: | ||
|
|
||
| def __init__(self, n): | ||
| self.parent = [i for i in range(n)] | ||
| self.count = n | ||
|
|
||
| def find(self, x): | ||
| while x != self.parent[x]: | ||
| self.parent[x] = self.parent[self.parent[x]] | ||
| x = self.parent[x] | ||
| return x | ||
|
|
||
| def union(self, x, y): | ||
| root_x = self.find(x) | ||
| root_y = self.find(y) | ||
| if root_x == root_y: | ||
| return | ||
|
|
||
| self.parent[root_x] = root_y | ||
| self.count -= 1 | ||
|
|
||
| def is_connected(self, x, y): | ||
| return self.find(x) == self.find(y) | ||
|
|
||
|
|
||
| class Solution: | ||
| def Kruskal(self, edges, size): | ||
| union_find = UnionFind(size) | ||
|
|
||
| edges.sort(key=lambda x: x[2]) | ||
|
|
||
| res, cnt = 0, 1 | ||
| for x, y, dist in edges: | ||
| if union_find.is_connected(x, y): | ||
| continue | ||
| ans += dist | ||
| cnt += 1 | ||
| union_find.union(x, y) | ||
| if cnt == size - 1: | ||
| return ans | ||
| return ans | ||
|
|
||
| def minCostConnectPoints(self, points: List[List[int]]) -> int: | ||
| size = len(points) | ||
| edges = [] | ||
| for i in range(size): | ||
| xi, yi = points[i] | ||
| for j in range(i + 1, size): | ||
| xj, yj = points[j] | ||
| dist = abs(xi - xj) + abs(yi - yj) | ||
| edges.append([i, j, dist]) | ||
|
|
||
| ans = Solution().Kruskal(edges, size) | ||
| return ans | ||
|
|
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters