前两天写一篇长达 8000 子的关于动态规划的文章告别动态规划,连刷40道动规算法题,我总结了动规的套路
这篇文章更多讲解我平时做题的套路,不过由于篇幅过长,举了 4 个案例之后,没有讲解优化,今天这篇文章就来讲解下,对动态规划的优化如何下手,并且以前几天那篇文章的题作为例子直接讲优化,如果没看过的建议看一下(不看也行,我会直接给出题目以及没有优化前的代码):告别动态规划,连刷40道动规算法题,我总结了动规的套路
没错,80% 的动态规划题都可以画图,其中 80% 的题都可以通过画图一下子知道怎么优化,当然,DP 也有一些很难的题,想优化可没那么容易,不过,今天我要讲的,是属于不怎么难,且最常见,面试笔试最经常考的难度的题。
下面我们直接通过三道题目来讲解优化,你会发现,这些题,优化过后,代码只有细微的改变,你只要会一两道,可以说是会了 80% 的题。
上次那个青蛙跳台阶的 dp 题是可以把空间复杂度 O( n) 优化成 O(1),本来打算从这道题讲起的,但想了下,想要学习 dp 优化的感觉至少都是 小小大佬了,所以就不讲了,就从二维数组的 dp 讲起。
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
这是 leetcode 的 62 号题:https://leetcode-cn.com/problems/unique-paths/
这道题的 dp 转移公式是 dp[i] [j] = dp[i-1] [j] + dp[i] [j-1],代码如下
不懂的看我之前文章:告别动态规划,连刷40道动规算法题,我总结了动规的套路
public static int uniquePaths(int m, int n) {
if (m <= 0 || n <= 0) {
return 0;
}
int[][] dp = new int[m][n]; //
// 初始化
for(int i = 0; i < m; i++){
dp[i][0] = 1;
}
for(int i = 0; i < n; i++){
dp[0][i] = 1;
}
// 推导出 dp[m-1][n-1]
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}这种做法的空间复杂度是 O(n * m),下面我们来讲解如何优化成 O(n)。
dp[i] [j] 是一个二维矩阵,我们来画个二维矩阵的图,对矩阵进行初始化

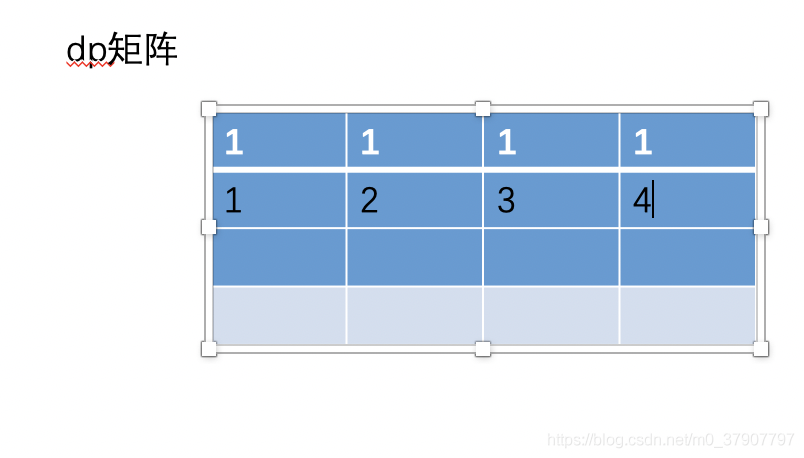
根据公式 dp[i][j] = dp[i-1][j] + dp[i][j-1],我们可以知道,当我们要计算第 i 行的值时,除了会用到第 i - 1 行外,其他第 1 至 第 i-2 行的值我们都是不需要用到的,也就是说,对于那部分用不到的值我们还有必要保存他们吗?
答是没必要,我们只需要用一个一维的 dp[] 来保存一行的历史记录就可以了。然后在计算机的过程中,不断着更新 dp[] 的值。单说估计你可能不好理解,下面我就手把手来演示下这个过程。
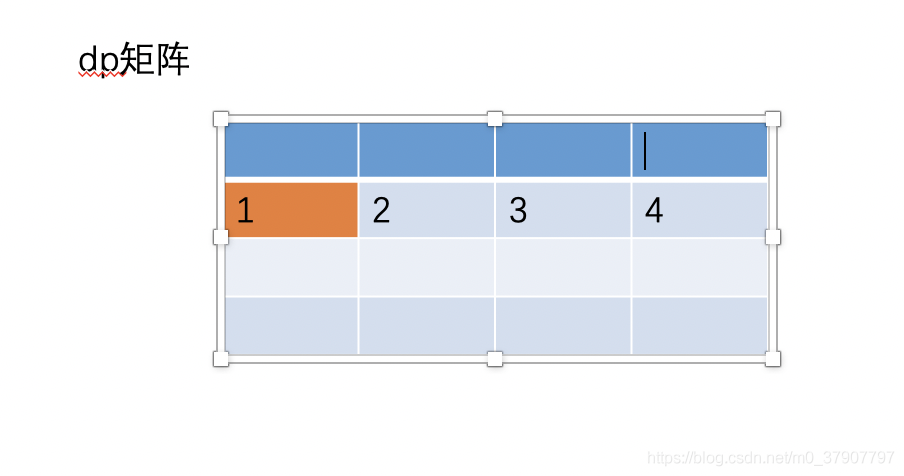
1、刚开始初始化第一行,此时 dp[0..n-1] 的值就是第一行的值。
2、接着我们来一边填充第二行的值一边更新 dp[i] 的值,一边把第一行的值抛弃掉。
为了方便描述,下面我们用arr (i,j)表示矩阵中第 i 行 第 j 列的值。从 0 开始哈,就是说有第 0 行。
(1)、显然,矩阵(1, 0) 的值相当于以往的初始化值,为 1。然后这个时候矩阵 (0,0)的值不在需要保存了,因为再也用不到了。
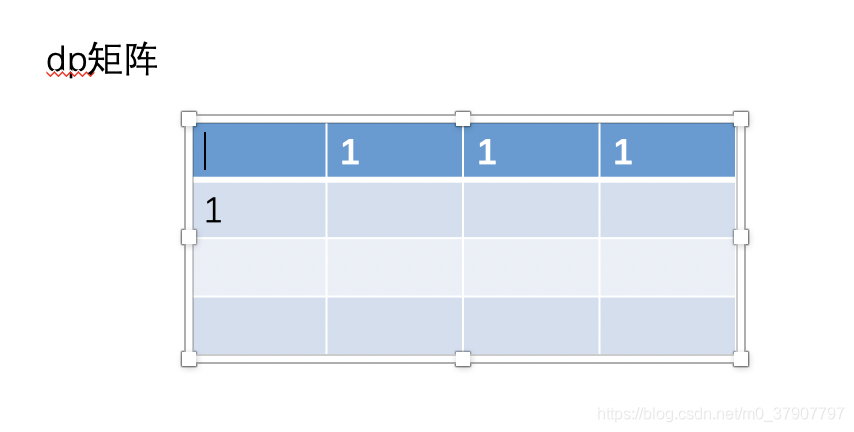
(2)、接着继续更新 (1, 1) 的值,根据之前的公式 (i, j) = (i-1, j) + (i, j- 1)。即 (1,1)=(0,1)+(1,0)=2。
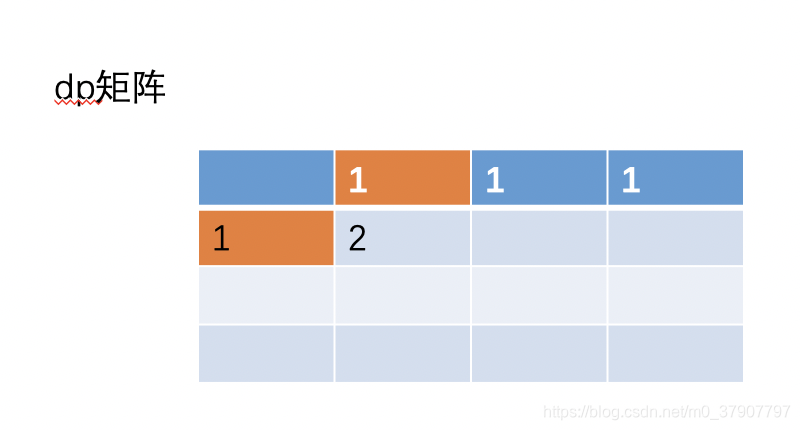
即 dp[1] = dp[1] + dp[0],而且还动态帮我们更新了 dp[1] 的值。因为刚开始 dp[i] 的保存第一行的值的,现在更新为保存第二行的值。

dp[i] = dp[i-1] + dp[i]
dp[i-1] 相当于之前的 dp[i-1][j],dp[i] 相当于之前的 dp[i][j-1]。
于是按照这个公式不停着填充到最后一行,结果如下:
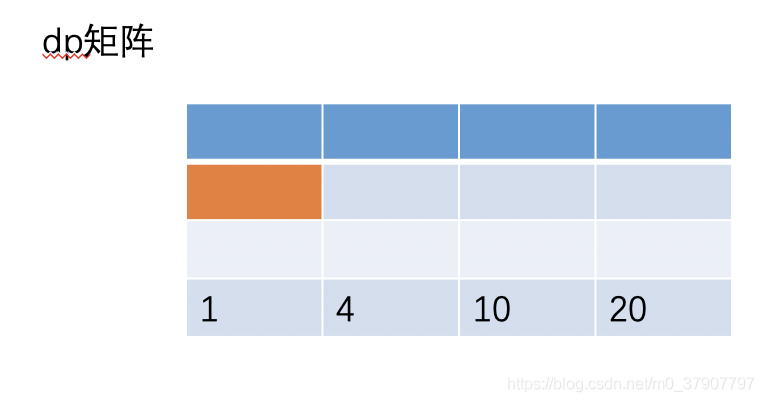
public static int uniquePaths(int m, int n) {
if (m <= 0 || n <= 0) {
return 0;
}
int[] dp = new int[n]; //
// 初始化
for(int i = 0; i < n; i++){
dp[i] = 1;
}
// 公式:dp[i] = dp[i-1] + dp[i]
for (int i = 1; i < m; i++) {
// 第 i 行第 0 列的初始值
dp[0] = 1;
for (int j = 1; j < n; j++) {
dp[j] = dp[j-1] + dp[j];
}
}
return dp[n-1];
}接着我们来看昨天的另外一道题,就是编辑矩阵,这道题的优化和这一道有一点点的不同,上面这道 dp[i][j] 依赖于 dp[i-1][j] 和 dp[i][j-1]。而还有一种情况就是 dp[i][j] 依赖于 dp[i-1][j],dp[i-1][j-1] 和 dp[i][j-1]。
问题描述
给定两个单词 word1 和 word2,计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符 删除一个字符 替换一个字符
示例:
输入: word1 = "horse", word2 = "ros"
输出: 3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')解答
昨天的代码如下所示,不懂的记得看之前的文章哈:告别动态规划,连刷40道动规算法题,我总结了动规的套路
public int minDistance(String word1, String word2) {
int n1 = word1.length();
int n2 = word2.length();
int[][] dp = new int[n1 + 1][n2 + 1];
// dp[0][0...n2]的初始值
for (int j = 1; j <= n2; j++)
dp[0][j] = dp[0][j - 1] + 1;
// dp[0...n1][0] 的初始值
for (int i = 1; i <= n1; i++) dp[i][0] = dp[i - 1][0] + 1;
// 通过公式推出 dp[n1][n2]
for (int i = 1; i <= n1; i++) {
for (int j = 1; j <= n2; j++) {
// 如果 word1[i] 与 word2[j] 相等。第 i 个字符对应下标是 i-1
if (word1.charAt(i - 1) == word2.charAt(j - 1)){
p[i][j] = dp[i - 1][j - 1];
}else {
dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1;
}
}
}
return dp[n1][n2];
}没有优化之间的空间复杂度为 O(n*m)
大家可以自己动手做下,按照上面的那个模式,你会优化吗?
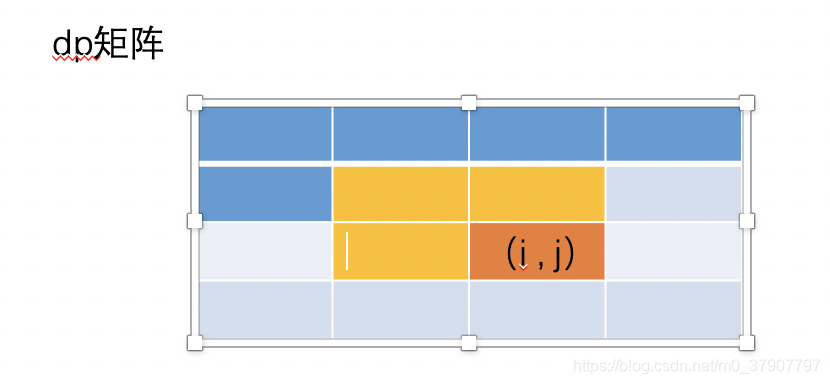
不过这个时候要注意,在上面的例子中,我们每次更新完 (i, j) 的值之后,就会把 (i, j-1) 的值抛弃,也就是说之前是一边更新 dp[i] 的值,一边把 dp[i] 的旧值抛弃的,不过在这道题中则不可以,因为我们还需要用到它。
哎呀,直接举例子看图吧,文字绕来绕去估计会绕晕你们。当我们要计算图中 (i,j) 的值的时候,在案例1 中,我们值需要用到 (i-1, j) 和 (i, j-1)。(看图中方格的颜色)
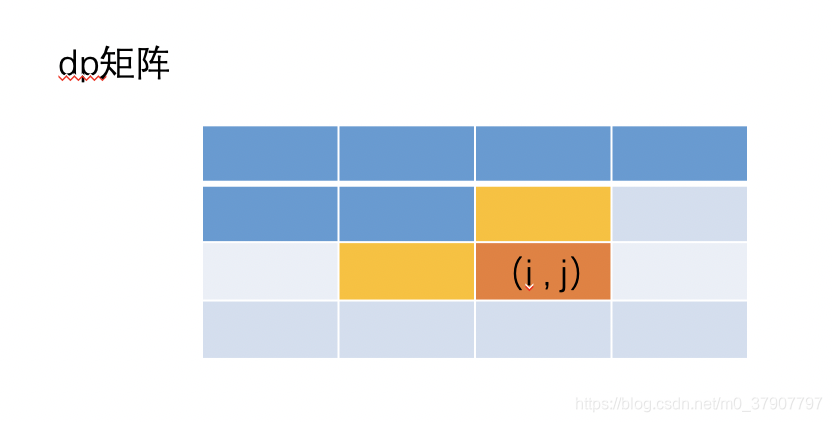
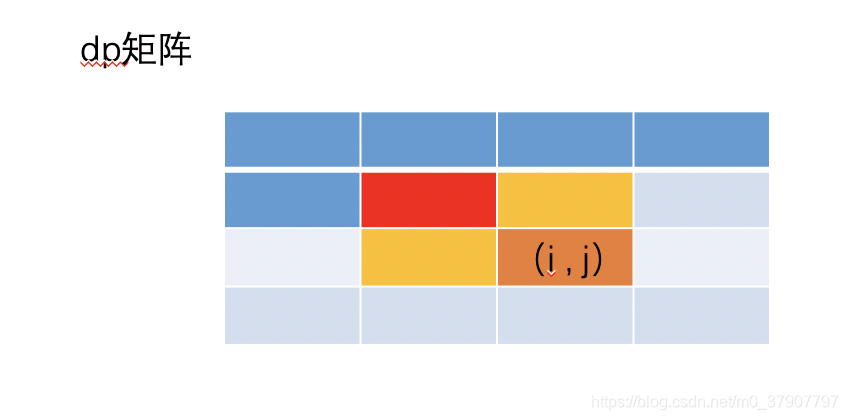
dp[i][j] = min(dp[i-1][j] , dp[i-1][j-1] , dp[i][j-1]) + 1
转化为一维的
dp[i] = min(dp[i-1], pre, dp[i]) + 1。
所以呢,案例2 其实和案例1 差别不大,就是多了个变量来临时保存。最终代码如下(但是初学者话,代码也没那么好写)
代码如下
public int minDistance(String word1, String word2) {
int n1 = word1.length();
int n2 = word2.length();
int[] dp = new int[n2 + 1];
// dp[0...n2]的初始值
for (int j = 0; j <= n2; j++)
dp[j] = j;
// dp[j] = min(dp[j-1], pre, dp[j]) + 1
for (int i = 1; i <= n1; i++) {
int temp = dp[0];
// 相当于初始化
dp[0] = i;
for (int j = 1; j <= n2; j++) {
// pre 相当于之前的 dp[i-1][j-1]
int pre = temp;
temp = dp[j];
// 如果 word1[i] 与 word2[j] 相等。第 i 个字符对应下标是 i-1
if (word1.charAt(i - 1) == word2.charAt(j - 1)){
dp[j] = pre;
}else {
dp[j] = Math.min(Math.min(dp[j - 1], pre), dp[j]) + 1;
}
// 保存要被抛弃的值
}
}
return dp[n2];
}基本 80% 的二维矩阵 dp 都可以像上面的方法一样优化成 一维矩阵的 dp,核心就是要画图,看他们的值依赖,当然,还有很多其他比较难的优化,但是,我遇到的题中,大部分都是我上面这种类型的优化。后面如何遇到其他的,我会作为案例来讲,今天就先讲最普遍最通用的优化方案。记住,画二维 dp 的矩阵图,然后看元素之间的值依赖,然后就可以很清晰着知道该如何优化了。
学习更多算法 + 计算机基础知识,欢迎关注我的微信公众号,每天准时推送技术干货