README.md

idol - The Mathematical Optimization Framework

Idol is a C++ library for mathematical optimization and complex decision making.

It is designed to help you build new algorithms easily for solving more and more challenging problems. It is a versatile and powerful tool that can be used to solve a wide range of optimization problems, including mixed-integer linear programming (MILP), quadratically constrained problems (MIQCQP and MIQP), bilevel problems (BO), robust optimization problems (RO and ARO) and many more.

• Documentation
• Using idol for Research?
• Examples
  • Branch-and-Price
  • Bilevel Problem (using coin-or/Mibs)
• Implemented Features
  • Branch-and-Bound
  • Column Generation and Branch-and-Price
  • External Solvers

Documentation

Visit our online documentation.

Using idol for Research?

If you are opting for idol in one of your research project and encounter some issues, please contact us at lefebvre(at)uni-trier.de.

Examples

Branch-and-Price

Look at how easy it is to implement a Branch-and-Price algorithm using idol.

const auto [model, decomposition] = create_model(); // Creates the model with an annotation for automatic decomposition

const auto sub_problem_specifications = 
        DantzigWolfe::SubProblem()
          .add_optimizer(Gurobi()); // Each sub-problem will be solved by Gurobi

const auto column_generation = 
        DantzigWolfeDecomposition(decomposition)
          .with_master_optimizer(Gurobi::ContinuousRelaxation()) // The master problem will be solved by Gurobi
          .with_default_sub_problem_spec(sub_problem_specifications);

const auto branch_and_bound =
        BranchAndBound()
          .with_node_selection_rule(BestBound()) // Nodes will be selected by the "best-bound" rule
          .with_branching_rule(MostInfeasible()) // Variables will be selected by the "most-fractional" rule
          .with_log_level(Info, Blue);

const auto branch_and_price = branch_and_bound + column_generation; // Embed the column generation in the Branch-and-Bound algorithm

model.use(branch_and_price);

model.optimize();

Bilevel Problem (using MibS)

Here, idol uses the external solver coin-or/MibS to solve a bilevel optimization problem with integer lower level.

/*
 This example is taken from "The Mixed Integer Linear Bilevel Programming Problem" (Moore and Bard, 1990).

    min -1 x + -10 y
    s.t.

    y in argmin { y :
        -25 x + 20 y <= 30,
        1 x + 2 y <= 10,
        2 x + -1 y <= 15,
        2 x + 10 y >= 15,
        y >= 0 and integer.
    }
    x >= 0 and integer.

 */

Env env;

// Define High Point Relaxation
Model high_point_relaxation(env);

auto x = high_point_relaxation.add_var(0, Inf, Integer, "x");
auto y = high_point_relaxation.add_var(0, Inf, Integer, "y");

high_point_relaxation.set_obj_expr(-x - 10 * y);
auto follower_c1 = high_point_relaxation.add_ctr(-25 * x + 20 * y <= 30);
auto follower_c2 = high_point_relaxation.add_ctr(x + 2 * y <= 10);
auto follower_c3 = high_point_relaxation.add_ctr(2 * x - y <= 15);
auto follower_c4 = high_point_relaxation.add_ctr(2 * x + 10 * y >= 15);

// Prepare bilevel description
Bilevel::LowerLevelDescription description(env);
description.set_follower_obj_expr(y);
description.set_follower_var(y);
description.set_follower_ctr(follower_c1);
description.set_follower_ctr(follower_c2);
description.set_follower_ctr(follower_c3);
description.set_follower_ctr(follower_c4);

// Use coin-or/MibS as external solver
high_point_relaxation.use(Bilevel::MibS(description));

// Optimize and print solution
high_point_relaxation.optimize();

std::cout << high_point_relaxation.get_status() << std::endl;
std::cout << high_point_relaxation.get_reason() << std::endl;
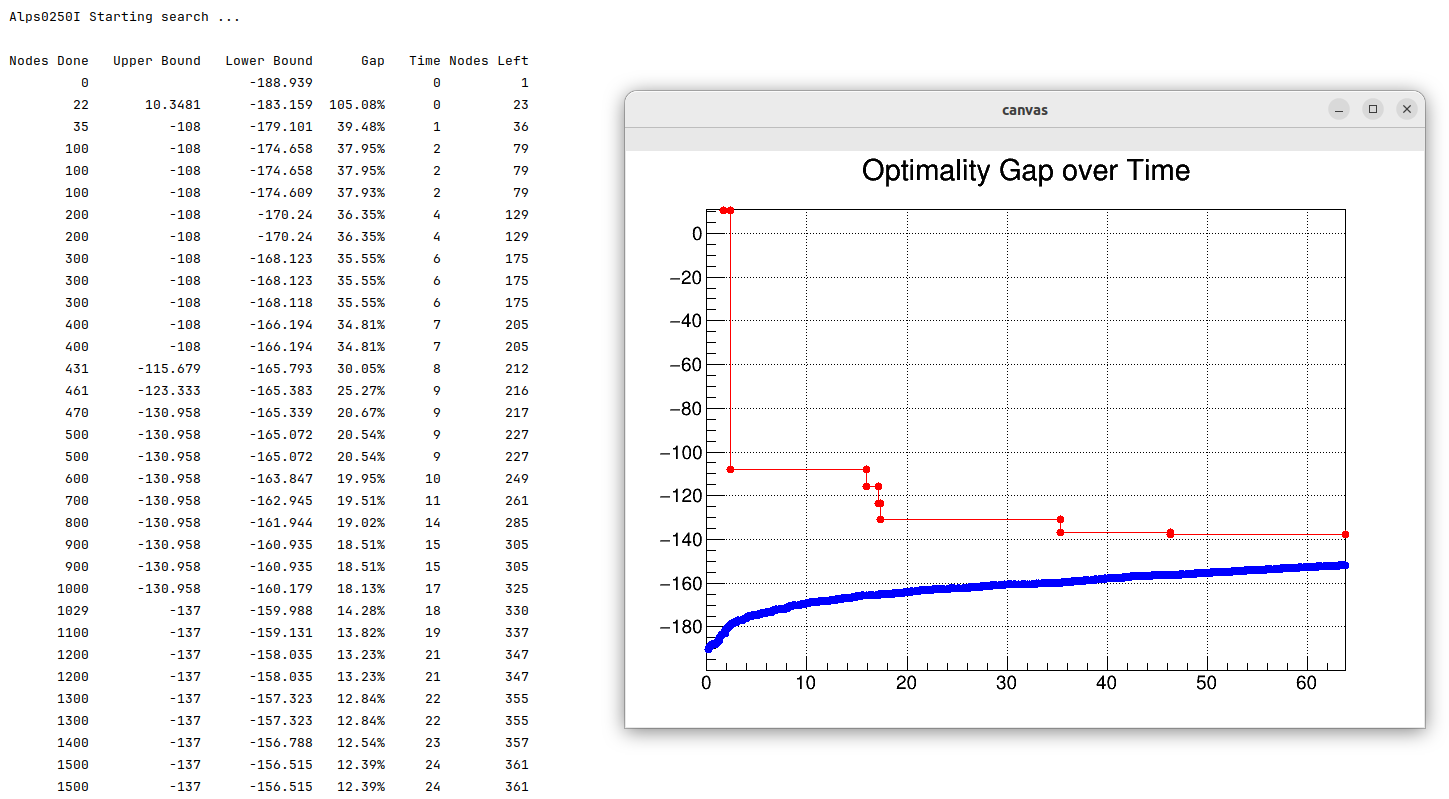
std::cout << save_primal(high_point_relaxation) << std::endl;

Idol can also be interfaced with ROOT to monitor the progress of your algorithm. For instance, here is a screenshot of the monitoring of MibS for a bilevel instance.

Implemented Features

Mixed-Integer Optimization

External Solvers

Idol can be used as a unified interface to several open-source or commercial solvers like

• Gurobi
• Mosek
• GLPK
• HiGHS
• coin-or/Osi --> Cplex, Symphony, Cbc

Branch-and-Bound

• Node selection rules: Best Bound, Worst Bound, Depth First, Best Estimate, Breadth First.
• Branching rules (for variable branching): Pseudo Cost, Strong Branching (with phases), Most Infeasible, Least Infeasible, First Found, Uniformly Random.
• Subtree exploration
• Heuristics (for variable branching): Simple Rounding, Relaxed Enforced Neighborhood, Local Branching
• Callbacks: User Cuts, Lazy Cuts

Column Generation and Branch-and-Price

• Automatic Dantzig-Wolfe reformulation
• Soft and hard branching available (i.e, branching on master or sub-problem)
• Stabilization by dual price smoothing: Wentges (1997), Neame (2000)
• Can solve sub-problems in parallel
• Supports pricing heuristics
• Heuristics: Integer Master

Bilevel Optimization

• Idol can solve optimistic mixed-integer bilevel problems using the external solver coin-or/MibS.

Two-stage Robust Optimization

Column-and-Constraint Generation (CCG)

• Generic implementation of the CCG algorithm for adjustable robust optimization problems.
• Trust region stabilization for problems with binary first stage decisions.
• Separation problem (max-min) solved by a bilevel solver.

Benchmark

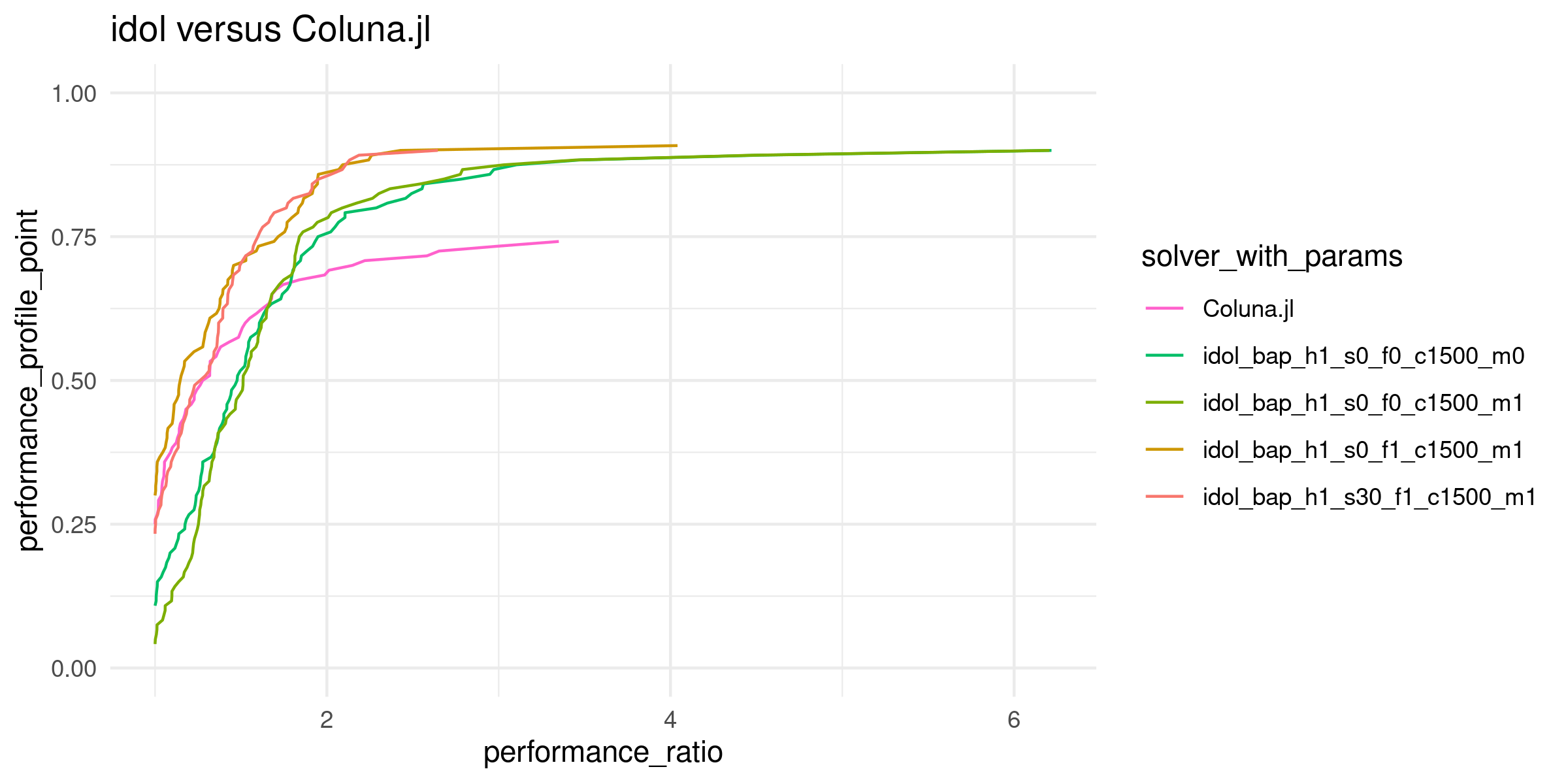
• A benchmark for the Branch-and-Price implementation is available for the Generalized Assignment Problem.
• A benchmark for the Branch-and-Bound implementation is available for the Knapsack Problem.

This is a performance profile computed according to Dolan, E., Moré, J. Benchmarking optimization software with performance profiles. Math. Program. 91, 201–213 (2002) https://doi.org/10.1007/s101070100263.

Miscellaneous

Versionning is compliant with Semantic versionning 2.0.0.