Skip to content

Latest commit

 

History

History
224 lines (184 loc) · 7.65 KB

README_EN.md

File metadata and controls

224 lines (184 loc) · 7.65 KB
comments difficulty edit_url rating source tags
true
Medium
1873
Weekly Contest 377 Q2
Array
Hash Table
Enumeration

2975. Maximum Square Area by Removing Fences From a Field

中文文档

Description

There is a large (m - 1) x (n - 1) rectangular field with corners at (1, 1) and (m, n) containing some horizontal and vertical fences given in arrays hFences and vFences respectively.

Horizontal fences are from the coordinates (hFences[i], 1) to (hFences[i], n) and vertical fences are from the coordinates (1, vFences[i]) to (m, vFences[i]).

Return the maximum area of a square field that can be formed by removing some fences (possibly none) or -1 if it is impossible to make a square field.

Since the answer may be large, return it modulo 109 + 7.

Note: The field is surrounded by two horizontal fences from the coordinates (1, 1) to (1, n) and (m, 1) to (m, n) and two vertical fences from the coordinates (1, 1) to (m, 1) and (1, n) to (m, n). These fences cannot be removed.

 

Example 1:

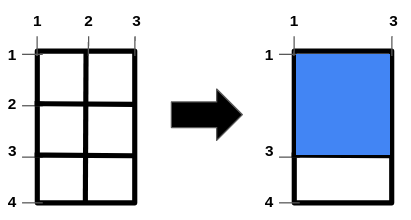
Input: m = 4, n = 3, hFences = [2,3], vFences = [2]
Output: 4
Explanation: Removing the horizontal fence at 2 and the vertical fence at 2 will give a square field of area 4.

Example 2:

Input: m = 6, n = 7, hFences = [2], vFences = [4]
Output: -1
Explanation: It can be proved that there is no way to create a square field by removing fences.

 

Constraints:

  • 3 <= m, n <= 109
  • 1 <= hFences.length, vFences.length <= 600
  • 1 < hFences[i] < m
  • 1 < vFences[i] < n
  • hFences and vFences are unique.

Solutions

Solution 1: Enumeration

We can enumerate any two horizontal fences $a$ and $b$ in $\textit{hFences}$, calculate the distance $d$ between $a$ and $b$, and record it in the hash table $hs$. Then, we enumerate any two vertical fences $c$ and $d$ in $\textit{vFences}$, calculate the distance $d$ between $c$ and $d$, and record it in the hash table $vs$. Finally, we traverse the hash table $hs$. If a certain distance $d$ in $hs$ also exists in the hash table $vs$, it indicates that there exists a square field with a side length of $d$, and the area is $d^2$. We just need to take the largest $d$ and calculate $d^2 \bmod 10^9 + 7$.

The time complexity is $O(h^2 + v^2)$, and the space complexity is $O(h^2 + v^2)$. Here, $h$ and $v$ are the lengths of $\textit{hFences}$ and $\textit{vFences}$, respectively.

Python3

class Solution:
    def maximizeSquareArea(
        self, m: int, n: int, hFences: List[int], vFences: List[int]
    ) -> int:
        def f(nums: List[int], k: int) -> Set[int]:
            nums.extend([1, k])
            nums.sort()
            return {b - a for a, b in combinations(nums, 2)}

        mod = 10**9 + 7
        hs = f(hFences, m)
        vs = f(vFences, n)
        ans = max(hs & vs, default=0)
        return ans**2 % mod if ans else -1

Java

class Solution {
    public int maximizeSquareArea(int m, int n, int[] hFences, int[] vFences) {
        Set<Integer> hs = f(hFences, m);
        Set<Integer> vs = f(vFences, n);
        hs.retainAll(vs);
        int ans = -1;
        final int mod = (int) 1e9 + 7;
        for (int x : hs) {
            ans = Math.max(ans, x);
        }
        return ans > 0 ? (int) (1L * ans * ans % mod) : -1;
    }

    private Set<Integer> f(int[] nums, int k) {
        int n = nums.length;
        nums = Arrays.copyOf(nums, n + 2);
        nums[n] = 1;
        nums[n + 1] = k;
        Arrays.sort(nums);
        Set<Integer> s = new HashSet<>();
        for (int i = 0; i < nums.length; ++i) {
            for (int j = 0; j < i; ++j) {
                s.add(nums[i] - nums[j]);
            }
        }
        return s;
    }
}

C++

class Solution {
public:
    int maximizeSquareArea(int m, int n, vector<int>& hFences, vector<int>& vFences) {
        auto f = [](vector<int>& nums, int k) {
            nums.push_back(k);
            nums.push_back(1);
            sort(nums.begin(), nums.end());
            unordered_set<int> s;
            for (int i = 0; i < nums.size(); ++i) {
                for (int j = 0; j < i; ++j) {
                    s.insert(nums[i] - nums[j]);
                }
            }
            return s;
        };
        auto hs = f(hFences, m);
        auto vs = f(vFences, n);
        int ans = 0;
        for (int h : hs) {
            if (vs.count(h)) {
                ans = max(ans, h);
            }
        }
        const int mod = 1e9 + 7;
        return ans > 0 ? 1LL * ans * ans % mod : -1;
    }
};

Go

func maximizeSquareArea(m int, n int, hFences []int, vFences []int) int {
	f := func(nums []int, k int) map[int]bool {
		nums = append(nums, 1, k)
		sort.Ints(nums)
		s := map[int]bool{}
		for i := 0; i < len(nums); i++ {
			for j := 0; j < i; j++ {
				s[nums[i]-nums[j]] = true
			}
		}
		return s
	}
	hs := f(hFences, m)
	vs := f(vFences, n)
	ans := 0
	for h := range hs {
		if vs[h] {
			ans = max(ans, h)
		}
	}
	if ans > 0 {
		return ans * ans % (1e9 + 7)
	}
	return -1
}

TypeScript

function maximizeSquareArea(m: number, n: number, hFences: number[], vFences: number[]): number {
    const f = (nums: number[], k: number): Set<number> => {
        nums.push(1, k);
        nums.sort((a, b) => a - b);
        const s: Set<number> = new Set();
        for (let i = 0; i < nums.length; ++i) {
            for (let j = 0; j < i; ++j) {
                s.add(nums[i] - nums[j]);
            }
        }
        return s;
    };
    const hs = f(hFences, m);
    const vs = f(vFences, n);
    let ans = 0;
    for (const h of hs) {
        if (vs.has(h)) {
            ans = Math.max(ans, h);
        }
    }
    return ans ? Number(BigInt(ans) ** 2n % 1000000007n) : -1;
}