comments

difficulty

edit_url

rating

source

2267. 检查是否有合法括号字符串路径

English Version

题目描述

一个括号字符串是一个非空且只包含 '(' 和 ')' 的字符串。如果下面任意条件为真，那么这个括号字符串就是 合法的 。

字符串是 () 。
字符串可以表示为 AB（A 连接 B），A 和 B 都是合法括号序列。
字符串可以表示为 (A) ，其中 A 是合法括号序列。

给你一个 m x n 的括号网格图矩阵 grid 。网格图中一个 合法括号路径 是满足以下所有条件的一条路径：

路径开始于左上角格子 (0, 0) 。
路径结束于右下角格子 (m - 1, n - 1) 。
路径每次只会向下或者向右移动。
路径经过的格子组成的括号字符串是合法的。

如果网格图中存在一条 合法括号路径 ，请返回 true ，否则返回 false 。

示例 1：

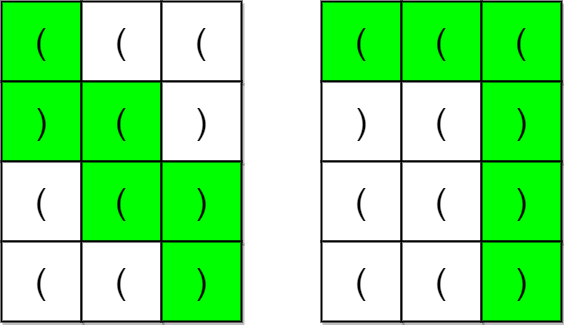
输入：grid = [["(","(","("],[")","(",")"],["(","(",")"],["(","(",")"]]
输出：true
解释：上图展示了两条路径，它们都是合法括号字符串路径。
第一条路径得到的合法字符串是 "()(())" 。
第二条路径得到的合法字符串是 "((()))" 。
注意可能有其他的合法括号字符串路径。

示例 2：

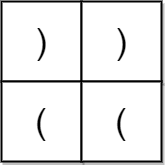
输入：grid = [[")",")"],["(","("]]
输出：false
解释：两条可行路径分别得到 "))(" 和 ")((" 。由于它们都不是合法括号字符串，我们返回 false 。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 100
grid[i][j] 要么是 '(' ，要么是 ')' 。

解法

方法一：DFS + 剪枝

我们记矩阵的行数为 $m$，列数为 $n$。

如果 $m + n - 1$ 为奇数，或者左上角和右下角的括号不匹配，那么一定不存在合法路径，直接返回 $\text{false}$。

否则，我们设计一个函数 $\textit{dfs}(i, j, k)$，表示从 $(i, j)$ 出发，且当前括号的平衡度为 $k$，是否存在合法路径。其中，平衡度 $k$ 的定义为：从 $(0, 0)$ 到 $(i, j)$ 的路径中，左括号的个数减去右括号的个数。

如果平衡度 $k$ 小于 $0$ 或者大于 $m + n - i - j$，那么一定不存在合法路径，直接返回 $\text{false}$。如果 $(i, j)$ 正好是右下角的格子，那么只有当 $k = 0$ 时才存在合法路径。否则，我们枚举 $(i, j)$ 的下一个格子 $(x, y)$，如果 $(x, y)$ 是合法的格子且 $\textit{dfs}(x, y, k)$ 为 $\text{true}$，那么就存在合法路径。

时间复杂度 $O(m \times n \times (m + n))$，空间复杂度 $O(m \times n \times (m + n))$。其中 $m$ 和 $n$ 分别是矩阵的行数和列数。

Python3

class Solution:
    def hasValidPath(self, grid: List[List[str]]) -> bool:
        @cache
        def dfs(i: int, j: int, k: int) -> bool:
            d = 1 if grid[i][j] == "(" else -1
            k += d
            if k < 0 or k > m - i + n - j:
                return False
            if i == m - 1 and j == n - 1:
                return k == 0
            for a, b in pairwise((0, 1, 0)):
                x, y = i + a, j + b
                if 0 <= x < m and 0 <= y < n and dfs(x, y, k):
                    return True
            return False

        m, n = len(grid), len(grid[0])
        if (m + n - 1) % 2 or grid[0][0] == ")" or grid[m - 1][n - 1] == "(":
            return False
        return dfs(0, 0, 0)

Java

class Solution {
    private int m, n;
    private char[][] grid;
    private boolean[][][] vis;

    public boolean hasValidPath(char[][] grid) {
        m = grid.length;
        n = grid[0].length;
        if ((m + n - 1) % 2 == 1 || grid[0][0] == ')' || grid[m - 1][n - 1] == '(') {
            return false;
        }
        this.grid = grid;
        vis = new boolean[m][n][m + n];
        return dfs(0, 0, 0);
    }

    private boolean dfs(int i, int j, int k) {
        if (vis[i][j][k]) {
            return false;
        }
        vis[i][j][k] = true;
        k += grid[i][j] == '(' ? 1 : -1;
        if (k < 0 || k > m - i + n - j) {
            return false;
        }
        if (i == m - 1 && j == n - 1) {
            return k == 0;
        }
        final int[] dirs = {1, 0, 1};
        for (int d = 0; d < 2; ++d) {
            int x = i + dirs[d], y = j + dirs[d + 1];
            if (x >= 0 && x < m && y >= 0 && y < n && dfs(x, y, k)) {
                return true;
            }
        }
        return false;
    }
}

C++

class Solution {
public:
    bool hasValidPath(vector<vector<char>>& grid) {
        int m = grid.size(), n = grid[0].size();
        if ((m + n - 1) % 2 || grid[0][0] == ')' || grid[m - 1][n - 1] == '(') {
            return false;
        }
        bool vis[m][n][m + n];
        memset(vis, false, sizeof(vis));
        int dirs[3] = {1, 0, 1};
        auto dfs = [&](this auto&& dfs, int i, int j, int k) -> bool {
            if (vis[i][j][k]) {
                return false;
            }
            vis[i][j][k] = true;
            k += grid[i][j] == '(' ? 1 : -1;
            if (k < 0 || k > m - i + n - j) {
                return false;
            }
            if (i == m - 1 && j == n - 1) {
                return k == 0;
            }
            for (int d = 0; d < 2; ++d) {
                int x = i + dirs[d], y = j + dirs[d + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && dfs(x, y, k)) {
                    return true;
                }
            }
            return false;
        };
        return dfs(0, 0, 0);
    }
};

Go

func hasValidPath(grid [][]byte) bool {
	m, n := len(grid), len(grid[0])
	if (m+n-1)%2 == 1 || grid[0][0] == ')' || grid[m-1][n-1] == '(' {
		return false
	}
	vis := make([][][]bool, m)
	for i := range vis {
		vis[i] = make([][]bool, n)
		for j := range vis[i] {
			vis[i][j] = make([]bool, m+n)
		}
	}
	dirs := [3]int{1, 0, 1}
	var dfs func(i, j, k int) bool
	dfs = func(i, j, k int) bool {
		if vis[i][j][k] {
			return false
		}
		vis[i][j][k] = true
		if grid[i][j] == '(' {
			k++
		} else {
			k--
		}
		if k < 0 || k > m-i+n-j {
			return false
		}
		if i == m-1 && j == n-1 {
			return k == 0
		}
		for d := 0; d < 2; d++ {
			x, y := i+dirs[d], j+dirs[d+1]
			if x >= 0 && x < m && y >= 0 && y < n && dfs(x, y, k) {
				return true
			}
		}
		return false
	}
	return dfs(0, 0, 0)
}

TypeScript

function hasValidPath(grid: string[][]): boolean {
    const m = grid.length,
        n = grid[0].length;

    if ((m + n - 1) % 2 || grid[0][0] === ')' || grid[m - 1][n - 1] === '(') {
        return false;
    }

    const vis: boolean[][][] = Array.from({ length: m }, () =>
        Array.from({ length: n }, () => Array(m + n).fill(false)),
    );
    const dirs = [1, 0, 1];

    const dfs = (i: number, j: number, k: number): boolean => {
        if (vis[i][j][k]) {
            return false;
        }

        vis[i][j][k] = true;
        k += grid[i][j] === '(' ? 1 : -1;

        if (k < 0 || k > m - i + n - j) {
            return false;
        }

        if (i === m - 1 && j === n - 1) {
            return k === 0;
        }

        for (let d = 0; d < 2; ++d) {
            const x = i + dirs[d],
                y = j + dirs[d + 1];
            if (x >= 0 && x < m && y >= 0 && y < n && dfs(x, y, k)) {
                return true;
            }
        }

        return false;
    };

    return dfs(0, 0, 0);
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README.md

README.md

2267. 检查是否有合法括号字符串路径

题目描述

解法

方法一：DFS + 剪枝

Python3

Java

C++

Go

TypeScript

Files

README.md

Latest commit

History

README.md

File metadata and controls

2267. 检查是否有合法括号字符串路径

题目描述

解法

方法一：DFS + 剪枝

Python3

Java

C++

Go

TypeScript