| comments | difficulty | edit_url | rating | source | tags | |
|---|---|---|---|---|---|---|
true |
Hard |
2241 |
Weekly Contest 160 Q4 |
|
Given a rectangle of size n x m, return the minimum number of integer-sided squares that tile the rectangle.
Example 1:
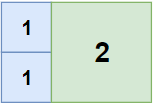
Input: n = 2, m = 3 Output: 3 Explanation:3squares are necessary to cover the rectangle.2(squares of1x1)1(square of2x2)
Example 2:
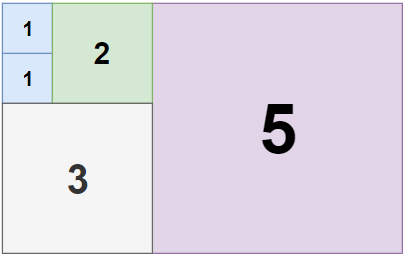
Input: n = 5, m = 8 Output: 5
Example 3:
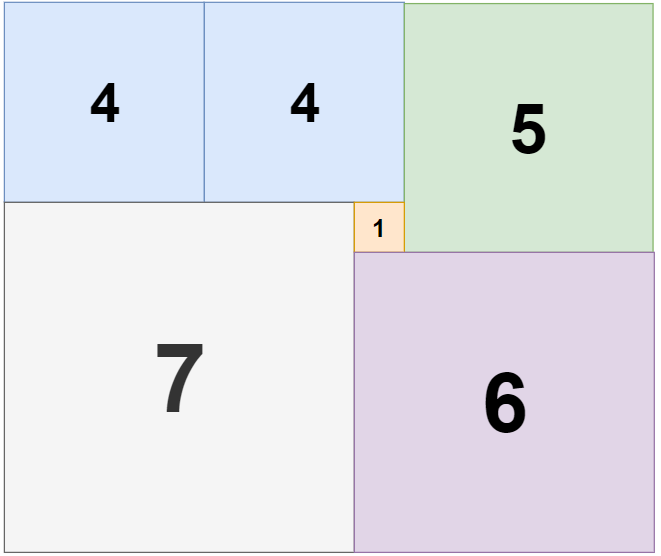
Input: n = 11, m = 13 Output: 6
Constraints:
1 <= n, m <= 13
We can perform recursive backtracking by position, during which we use a variable
- If
$j = m$ , i.e., the$i$ -th row has been completely filled, then we recurse to the next row, i.e.,$(i + 1, 0)$ . - If
$i = n$ , it means that all positions have been filled, we update the answer and return. - If the current position
$(i, j)$ has been filled, then directly recurse to the next position$(i, j + 1)$ . - Otherwise, we enumerate the maximum square side length
$w$ that the current position$(i, j)$ can fill, and fill all positions from$(i, j)$ to$(i + w - 1, j + w - 1)$ , then recurse to the next position$(i, j + w)$ . When backtracking, we need to clear all positions from$(i, j)$ to$(i + w - 1, j + w - 1)$ .
Since each position only has two states: filled or not filled, we can use an integer to represent the current state. We use an integer array
class Solution:
def tilingRectangle(self, n: int, m: int) -> int:
def dfs(i: int, j: int, t: int):
nonlocal ans
if j == m:
i += 1
j = 0
if i == n:
ans = t
return
if filled[i] >> j & 1:
dfs(i, j + 1, t)
elif t + 1 < ans:
r = c = 0
for k in range(i, n):
if filled[k] >> j & 1:
break
r += 1
for k in range(j, m):
if filled[i] >> k & 1:
break
c += 1
mx = r if r < c else c
for w in range(1, mx + 1):
for k in range(w):
filled[i + w - 1] |= 1 << (j + k)
filled[i + k] |= 1 << (j + w - 1)
dfs(i, j + w, t + 1)
for x in range(i, i + mx):
for y in range(j, j + mx):
filled[x] ^= 1 << y
ans = n * m
filled = [0] * n
dfs(0, 0, 0)
return ansclass Solution {
private int n;
private int m;
private int[] filled;
private int ans;
public int tilingRectangle(int n, int m) {
this.n = n;
this.m = m;
ans = n * m;
filled = new int[n];
dfs(0, 0, 0);
return ans;
}
private void dfs(int i, int j, int t) {
if (j == m) {
++i;
j = 0;
}
if (i == n) {
ans = t;
return;
}
if ((filled[i] >> j & 1) == 1) {
dfs(i, j + 1, t);
} else if (t + 1 < ans) {
int r = 0, c = 0;
for (int k = i; k < n; ++k) {
if ((filled[k] >> j & 1) == 1) {
break;
}
++r;
}
for (int k = j; k < m; ++k) {
if ((filled[i] >> k & 1) == 1) {
break;
}
++c;
}
int mx = Math.min(r, c);
for (int w = 1; w <= mx; ++w) {
for (int k = 0; k < w; ++k) {
filled[i + w - 1] |= 1 << (j + k);
filled[i + k] |= 1 << (j + w - 1);
}
dfs(i, j + w, t + 1);
}
for (int x = i; x < i + mx; ++x) {
for (int y = j; y < j + mx; ++y) {
filled[x] ^= 1 << y;
}
}
}
}
}class Solution {
public:
int tilingRectangle(int n, int m) {
memset(filled, 0, sizeof(filled));
this->n = n;
this->m = m;
ans = n * m;
dfs(0, 0, 0);
return ans;
}
private:
int filled[13];
int n, m;
int ans;
void dfs(int i, int j, int t) {
if (j == m) {
++i;
j = 0;
}
if (i == n) {
ans = t;
return;
}
if (filled[i] >> j & 1) {
dfs(i, j + 1, t);
} else if (t + 1 < ans) {
int r = 0, c = 0;
for (int k = i; k < n; ++k) {
if (filled[k] >> j & 1) {
break;
}
++r;
}
for (int k = j; k < m; ++k) {
if (filled[i] >> k & 1) {
break;
}
++c;
}
int mx = min(r, c);
for (int w = 1; w <= mx; ++w) {
for (int k = 0; k < w; ++k) {
filled[i + w - 1] |= 1 << (j + k);
filled[i + k] |= 1 << (j + w - 1);
}
dfs(i, j + w, t + 1);
}
for (int x = i; x < i + mx; ++x) {
for (int y = j; y < j + mx; ++y) {
filled[x] ^= 1 << y;
}
}
}
}
};func tilingRectangle(n int, m int) int {
ans := n * m
filled := make([]int, n)
var dfs func(i, j, t int)
dfs = func(i, j, t int) {
if j == m {
i++
j = 0
}
if i == n {
ans = t
return
}
if filled[i]>>j&1 == 1 {
dfs(i, j+1, t)
} else if t+1 < ans {
var r, c int
for k := i; k < n; k++ {
if filled[k]>>j&1 == 1 {
break
}
r++
}
for k := j; k < m; k++ {
if filled[i]>>k&1 == 1 {
break
}
c++
}
mx := min(r, c)
for w := 1; w <= mx; w++ {
for k := 0; k < w; k++ {
filled[i+w-1] |= 1 << (j + k)
filled[i+k] |= 1 << (j + w - 1)
}
dfs(i, j+w, t+1)
}
for x := i; x < i+mx; x++ {
for y := j; y < j+mx; y++ {
filled[x] ^= 1 << y
}
}
}
}
dfs(0, 0, 0)
return ans
}function tilingRectangle(n: number, m: number): number {
let ans = n * m;
const filled: number[] = new Array(n).fill(0);
const dfs = (i: number, j: number, t: number) => {
if (j === m) {
++i;
j = 0;
}
if (i === n) {
ans = t;
return;
}
if ((filled[i] >> j) & 1) {
dfs(i, j + 1, t);
} else if (t + 1 < ans) {
let [r, c] = [0, 0];
for (let k = i; k < n; ++k) {
if ((filled[k] >> j) & 1) {
break;
}
++r;
}
for (let k = j; k < m; ++k) {
if ((filled[i] >> k) & 1) {
break;
}
++c;
}
const mx = Math.min(r, c);
for (let w = 1; w <= mx; ++w) {
for (let k = 0; k < w; ++k) {
filled[i + w - 1] |= 1 << (j + k);
filled[i + k] |= 1 << (j + w - 1);
}
dfs(i, j + w, t + 1);
}
for (let x = i; x < i + mx; ++x) {
for (let y = j; y < j + mx; ++y) {
filled[x] ^= 1 << y;
}
}
}
};
dfs(0, 0, 0);
return ans;
}class Solution:
def tilingRectangle(self, n: int, m: int) -> int:
def dfs(i: int, j: int, t: int):
nonlocal ans
if j == m:
i += 1
j = 0
if i == n:
ans = t
return
if filled[i] >> j & 1:
dfs(i, j + 1, t)
elif t + 1 < ans:
r = c = 0
for k in range(i, n):
if filled[k] >> j & 1:
break
r += 1
for k in range(j, m):
if filled[i] >> k & 1:
break
c += 1
mx = min(r, c)
for x in range(i, i + mx):
for y in range(j, j + mx):
filled[x] |= 1 << y
for w in range(mx, 0, -1):
dfs(i, j + w, t + 1)
for k in range(w):
filled[i + w - 1] ^= 1 << (j + k)
if k < w - 1:
filled[i + k] ^= 1 << (j + w - 1)
ans = n * m
filled = [0] * n
dfs(0, 0, 0)
return ansclass Solution {
private int n;
private int m;
private int[] filled;
private int ans;
public int tilingRectangle(int n, int m) {
this.n = n;
this.m = m;
ans = n * m;
filled = new int[n];
dfs(0, 0, 0);
return ans;
}
private void dfs(int i, int j, int t) {
if (j == m) {
++i;
j = 0;
}
if (i == n) {
ans = t;
return;
}
if ((filled[i] >> j & 1) == 1) {
dfs(i, j + 1, t);
} else if (t + 1 < ans) {
int r = 0, c = 0;
for (int k = i; k < n; ++k) {
if ((filled[k] >> j & 1) == 1) {
break;
}
++r;
}
for (int k = j; k < m; ++k) {
if ((filled[i] >> k & 1) == 1) {
break;
}
++c;
}
int mx = Math.min(r, c);
for (int x = i; x < i + mx; ++x) {
for (int y = j; y < j + mx; ++y) {
filled[x] |= 1 << y;
}
}
for (int w = mx; w > 0; --w) {
dfs(i, j + w, t + 1);
for (int k = 0; k < w; ++k) {
filled[i + w - 1] ^= 1 << (j + k);
if (k < w - 1) {
filled[i + k] ^= 1 << (j + w - 1);
}
}
}
}
}
}class Solution {
public:
int tilingRectangle(int n, int m) {
memset(filled, 0, sizeof(filled));
this->n = n;
this->m = m;
ans = n * m;
dfs(0, 0, 0);
return ans;
}
private:
int filled[13];
int n, m;
int ans;
void dfs(int i, int j, int t) {
if (j == m) {
++i;
j = 0;
}
if (i == n) {
ans = t;
return;
}
if (filled[i] >> j & 1) {
dfs(i, j + 1, t);
} else if (t + 1 < ans) {
int r = 0, c = 0;
for (int k = i; k < n; ++k) {
if (filled[k] >> j & 1) {
break;
}
++r;
}
for (int k = j; k < m; ++k) {
if (filled[i] >> k & 1) {
break;
}
++c;
}
int mx = min(r, c);
for (int x = i; x < i + mx; ++x) {
for (int y = j; y < j + mx; ++y) {
filled[x] |= 1 << y;
}
}
for (int w = mx; w; --w) {
dfs(i, j + w, t + 1);
for (int k = 0; k < w; ++k) {
filled[i + w - 1] ^= 1 << (j + k);
if (k < w - 1) {
filled[i + k] ^= 1 << (j + w - 1);
}
}
}
}
}
};func tilingRectangle(n int, m int) int {
ans := n * m
filled := make([]int, n)
var dfs func(i, j, t int)
dfs = func(i, j, t int) {
if j == m {
i++
j = 0
}
if i == n {
ans = t
return
}
if filled[i]>>j&1 == 1 {
dfs(i, j+1, t)
} else if t+1 < ans {
var r, c int
for k := i; k < n; k++ {
if filled[k]>>j&1 == 1 {
break
}
r++
}
for k := j; k < m; k++ {
if filled[i]>>k&1 == 1 {
break
}
c++
}
mx := min(r, c)
for x := i; x < i+mx; x++ {
for y := j; y < j+mx; y++ {
filled[x] |= 1 << y
}
}
for w := mx; w > 0; w-- {
dfs(i, j+w, t+1)
for k := 0; k < w; k++ {
filled[i+w-1] ^= 1 << (j + k)
if k < w-1 {
filled[i+k] ^= 1 << (j + w - 1)
}
}
}
}
}
dfs(0, 0, 0)
return ans
}function tilingRectangle(n: number, m: number): number {
let ans = n * m;
const filled: number[] = new Array(n).fill(0);
const dfs = (i: number, j: number, t: number) => {
if (j === m) {
++i;
j = 0;
}
if (i === n) {
ans = t;
return;
}
if ((filled[i] >> j) & 1) {
dfs(i, j + 1, t);
} else if (t + 1 < ans) {
let [r, c] = [0, 0];
for (let k = i; k < n; ++k) {
if ((filled[k] >> j) & 1) {
break;
}
++r;
}
for (let k = j; k < m; ++k) {
if ((filled[i] >> k) & 1) {
break;
}
++c;
}
const mx = Math.min(r, c);
for (let x = i; x < i + mx; ++x) {
for (let y = j; y < j + mx; ++y) {
filled[x] |= 1 << y;
}
}
for (let w = mx; w > 0; --w) {
dfs(i, j + w, t + 1);
for (let k = 0; k < w; ++k) {
filled[i + w - 1] ^= 1 << (j + k);
if (k < w - 1) {
filled[i + k] ^= 1 << (j + w - 1);
}
}
}
}
};
dfs(0, 0, 0);
return ans;
}