| comments | difficulty | edit_url | rating | source | tags | |||
|---|---|---|---|---|---|---|---|---|
true |
Hard |
2022 |
Weekly Contest 156 Q4 |
|
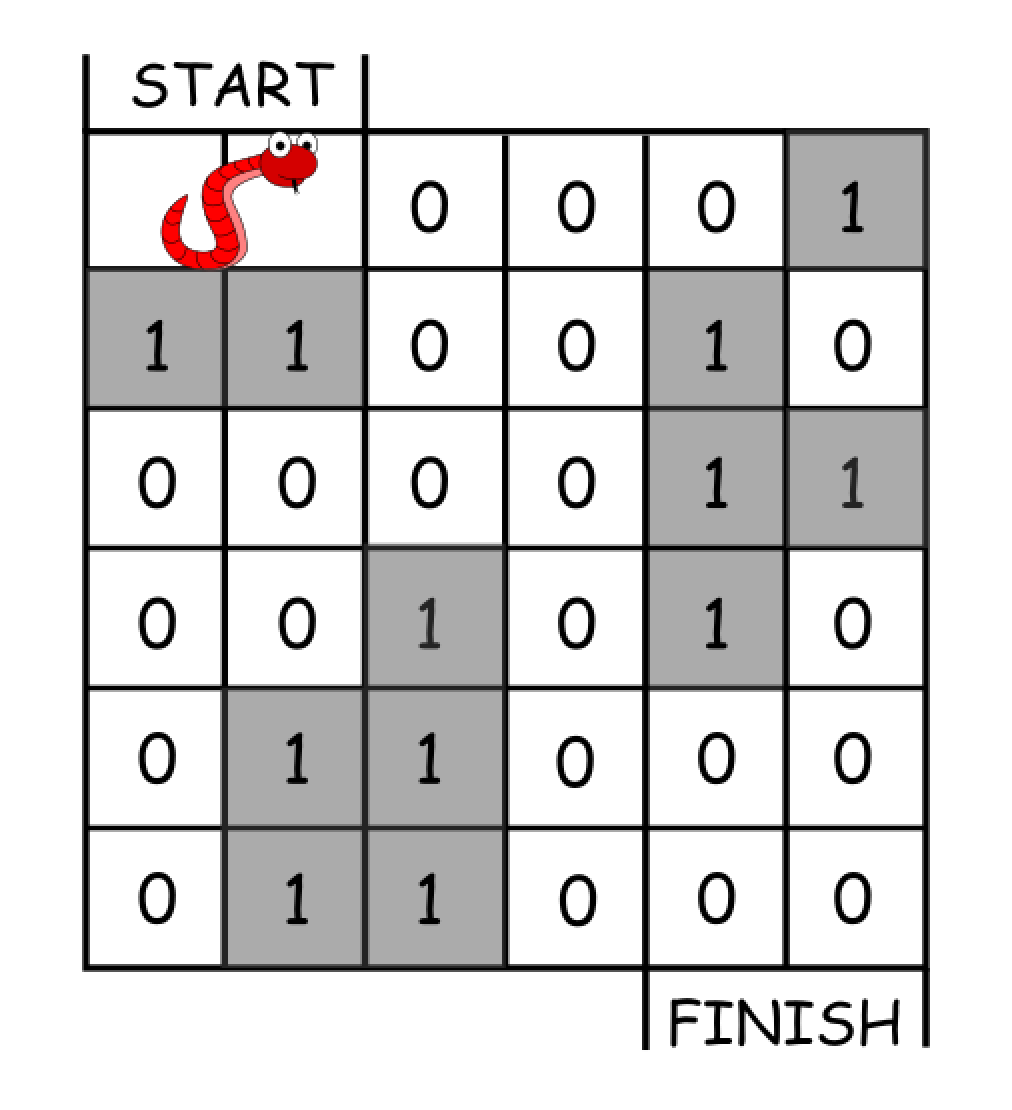
In an n*n grid, there is a snake that spans 2 cells and starts moving from the top left corner at (0, 0) and (0, 1). The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at (n-1, n-2) and (n-1, n-1).
In one move the snake can:
- Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
- Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
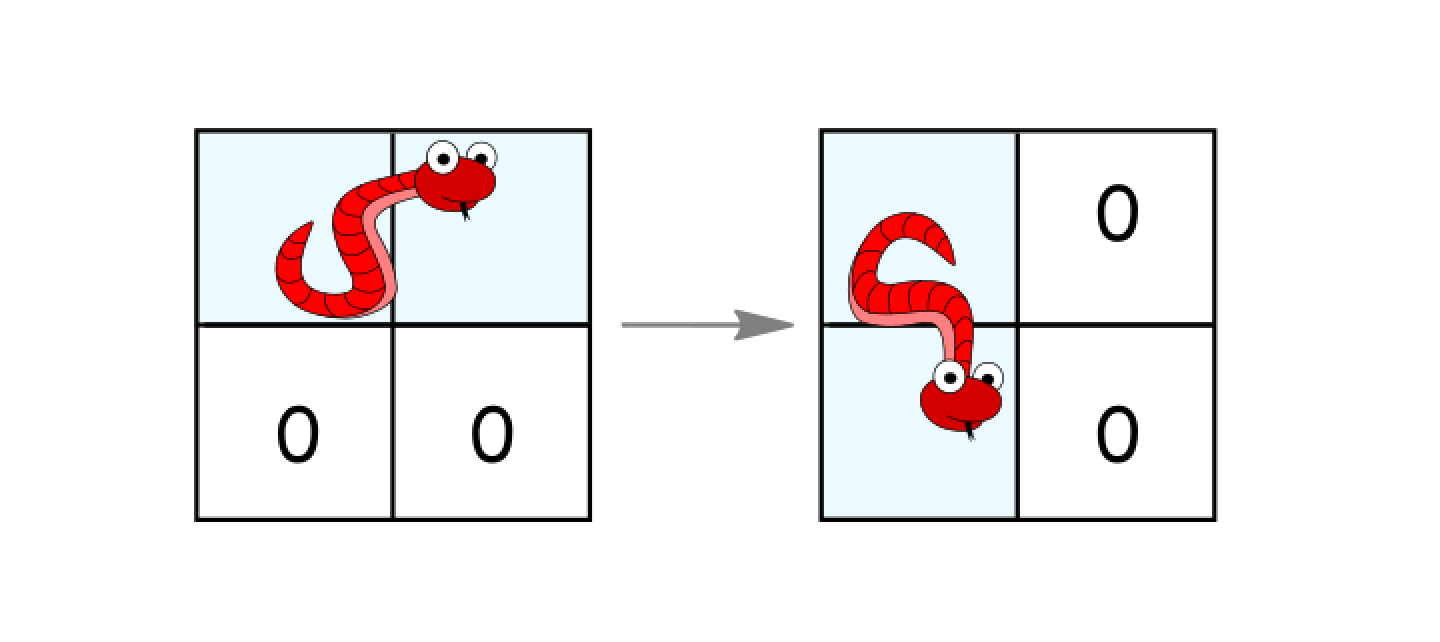
- Rotate clockwise if it's in a horizontal position and the two cells under it are both empty. In that case the snake moves from
(r, c)and(r, c+1)to(r, c)and(r+1, c).
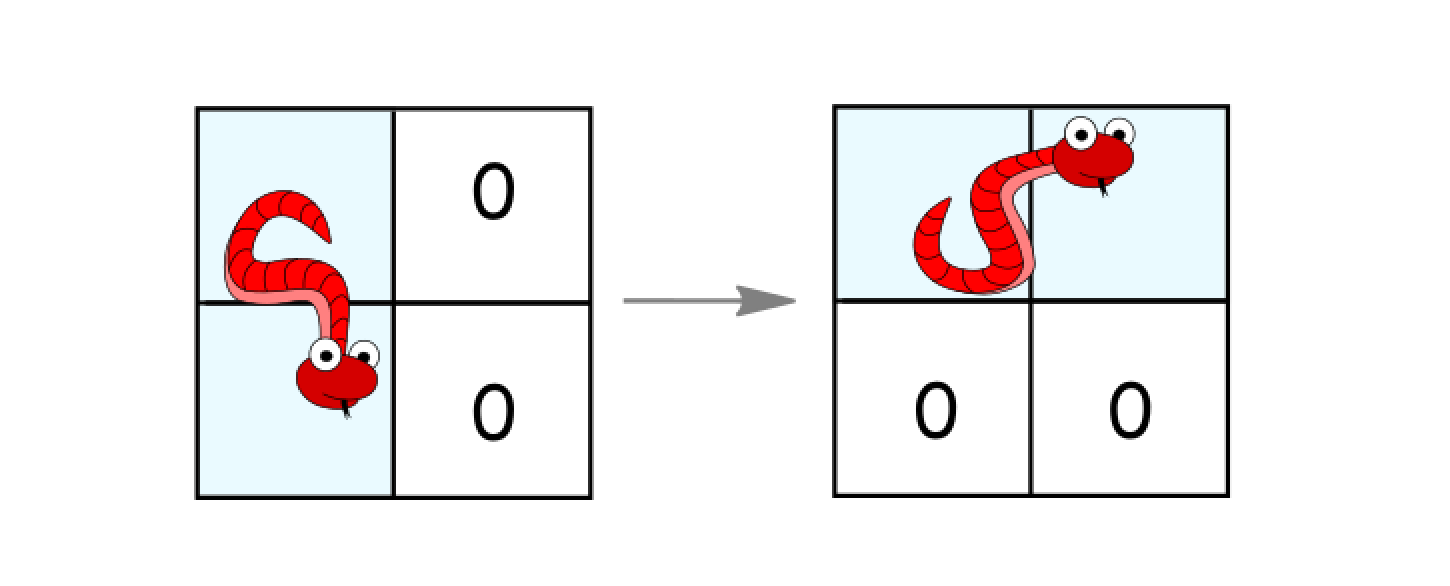
- Rotate counterclockwise if it's in a vertical position and the two cells to its right are both empty. In that case the snake moves from
(r, c)and(r+1, c)to(r, c)and(r, c+1).
Return the minimum number of moves to reach the target.
If there is no way to reach the target, return -1.
Example 1:
Input: grid = [[0,0,0,0,0,1],
[1,1,0,0,1,0],
[0,0,0,0,1,1],
[0,0,1,0,1,0],
[0,1,1,0,0,0],
[0,1,1,0,0,0]]
Output: 11
Explanation:
One possible solution is [right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down].
Example 2:
Input: grid = [[0,0,1,1,1,1], [0,0,0,0,1,1], [1,1,0,0,0,1], [1,1,1,0,0,1], [1,1,1,0,0,1], [1,1,1,0,0,0]] Output: 9
Constraints:
2 <= n <= 1000 <= grid[i][j] <= 1- It is guaranteed that the snake starts at empty cells.
The problem asks for the minimum number of moves for the snake to reach the target position from the starting position. We consider using Breadth-First Search (BFS) to solve it.
We define the following data structures or variables:
- Queue
$q$ : Stores the current position of the snake. Each position is a tuple$(a, b)$ , where$a$ represents the tail position of the snake, and$b$ represents the head position of the snake. Initially, we add the position$(0, 1)$ to the queue$q$ . If we flatten the 2D maze into a 1D array, then the position$(0, 1)$ represents the two cells with indices$0$ and$1$ in the 1D array. - Target position
$target$ : The value is fixed at$(n^2 - 2, n^2 - 1)$ , which is the last two cells of the last row of the 2D maze. - Array or set
$vis$ : Stores whether the current position state of the snake has been visited. Each state is a tuple$(a, status)$ , where$a$ represents the tail position of the snake, and$status$ represents the current state of the snake, with values of$0$ or$1$ , representing the horizontal and vertical states of the snake, respectively. Initially, add the state of the starting position$(0, 1)$ to the set$vis$ . - Answer variable
$ans$ : Stores the number of moves for the snake to reach the target position from the starting position. Initially, it is$0$ .
We use BFS to solve it. Each time we take a position from the queue
Finally, if the queue
The time complexity is
class Solution:
def minimumMoves(self, grid: List[List[int]]) -> int:
def move(i1, j1, i2, j2):
if 0 <= i1 < n and 0 <= j1 < n and 0 <= i2 < n and 0 <= j2 < n:
a, b = i1 * n + j1, i2 * n + j2
status = 0 if i1 == i2 else 1
if (a, status) not in vis and grid[i1][j1] == 0 and grid[i2][j2] == 0:
q.append((a, b))
vis.add((a, status))
n = len(grid)
target = (n * n - 2, n * n - 1)
q = deque([(0, 1)])
vis = {(0, 0)}
ans = 0
while q:
for _ in range(len(q)):
a, b = q.popleft()
if (a, b) == target:
return ans
i1, j1 = a // n, a % n
i2, j2 = b // n, b % n
# 尝试向右平移(保持身体水平/垂直状态)
move(i1, j1 + 1, i2, j2 + 1)
# 尝试向下平移(保持身体水平/垂直状态)
move(i1 + 1, j1, i2 + 1, j2)
# 当前处于水平状态,且 grid[i1 + 1][j2] 无障碍,尝试顺时针旋转90°
if i1 == i2 and i1 + 1 < n and grid[i1 + 1][j2] == 0:
move(i1, j1, i1 + 1, j1)
# 当前处于垂直状态,且 grid[i2][j1 + 1] 无障碍,尝试逆时针旋转90°
if j1 == j2 and j1 + 1 < n and grid[i2][j1 + 1] == 0:
move(i1, j1, i1, j1 + 1)
ans += 1
return -1class Solution {
private int n;
private int[][] grid;
private boolean[][] vis;
private Deque<int[]> q = new ArrayDeque<>();
public int minimumMoves(int[][] grid) {
this.grid = grid;
n = grid.length;
vis = new boolean[n * n][2];
int[] target = {n * n - 2, n * n - 1};
q.offer(new int[] {0, 1});
vis[0][0] = true;
int ans = 0;
while (!q.isEmpty()) {
for (int k = q.size(); k > 0; --k) {
var p = q.poll();
if (p[0] == target[0] && p[1] == target[1]) {
return ans;
}
int i1 = p[0] / n, j1 = p[0] % n;
int i2 = p[1] / n, j2 = p[1] % n;
// 尝试向右平移(保持身体水平/垂直状态)
move(i1, j1 + 1, i2, j2 + 1);
// 尝试向下平移(保持身体水平/垂直状态)
move(i1 + 1, j1, i2 + 1, j2);
// 当前处于水平状态,且 grid[i1 + 1][j2] 无障碍,尝试顺时针旋转90°
if (i1 == i2 && i1 + 1 < n && grid[i1 + 1][j2] == 0) {
move(i1, j1, i1 + 1, j1);
}
// 当前处于垂直状态,且 grid[i2][j1 + 1] 无障碍,尝试逆时针旋转90°
if (j1 == j2 && j1 + 1 < n && grid[i2][j1 + 1] == 0) {
move(i1, j1, i1, j1 + 1);
}
}
++ans;
}
return -1;
}
private void move(int i1, int j1, int i2, int j2) {
if (i1 >= 0 && i1 < n && j1 >= 0 && j1 < n && i2 >= 0 && i2 < n && j2 >= 0 && j2 < n) {
int a = i1 * n + j1, b = i2 * n + j2;
int status = i1 == i2 ? 0 : 1;
if (!vis[a][status] && grid[i1][j1] == 0 && grid[i2][j2] == 0) {
q.offer(new int[] {a, b});
vis[a][status] = true;
}
}
}
}class Solution {
public:
int minimumMoves(vector<vector<int>>& grid) {
int n = grid.size();
auto target = make_pair(n * n - 2, n * n - 1);
queue<pair<int, int>> q;
q.emplace(0, 1);
bool vis[n * n][2];
memset(vis, 0, sizeof vis);
vis[0][0] = true;
auto move = [&](int i1, int j1, int i2, int j2) {
if (i1 >= 0 && i1 < n && j1 >= 0 && j1 < n && i2 >= 0 && i2 < n && j2 >= 0 && j2 < n) {
int a = i1 * n + j1, b = i2 * n + j2;
int status = i1 == i2 ? 0 : 1;
if (!vis[a][status] && grid[i1][j1] == 0 && grid[i2][j2] == 0) {
q.emplace(a, b);
vis[a][status] = true;
}
}
};
int ans = 0;
while (!q.empty()) {
for (int k = q.size(); k; --k) {
auto p = q.front();
q.pop();
if (p == target) {
return ans;
}
auto [a, b] = p;
int i1 = a / n, j1 = a % n;
int i2 = b / n, j2 = b % n;
// 尝试向右平移(保持身体水平/垂直状态)
move(i1, j1 + 1, i2, j2 + 1);
// 尝试向下平移(保持身体水平/垂直状态)
move(i1 + 1, j1, i2 + 1, j2);
// 当前处于水平状态,且 grid[i1 + 1][j2] 无障碍,尝试顺时针旋转90°
if (i1 == i2 && i1 + 1 < n && grid[i1 + 1][j2] == 0) {
move(i1, j1, i1 + 1, j1);
}
// 当前处于垂直状态,且 grid[i2][j1 + 1] 无障碍,尝试逆时针旋转90°
if (j1 == j2 && j1 + 1 < n && grid[i2][j1 + 1] == 0) {
move(i1, j1, i1, j1 + 1);
}
}
++ans;
}
return -1;
}
};func minimumMoves(grid [][]int) int {
n := len(grid)
type pair struct{ a, b int }
target := pair{n*n - 2, n*n - 1}
q := []pair{pair{0, 1}}
vis := make([][2]bool, n*n)
vis[0][0] = true
move := func(i1, j1, i2, j2 int) {
if i1 >= 0 && i1 < n && j1 >= 0 && j1 < n && i2 >= 0 && i2 < n && j2 >= 0 && j2 < n {
a, b := i1*n+j1, i2*n+j2
status := 1
if i1 == i2 {
status = 0
}
if !vis[a][status] && grid[i1][j1] == 0 && grid[i2][j2] == 0 {
q = append(q, pair{a, b})
vis[a][status] = true
}
}
}
ans := 0
for len(q) > 0 {
for k := len(q); k > 0; k-- {
p := q[0]
q = q[1:]
if p == target {
return ans
}
a, b := p.a, p.b
i1, j1 := a/n, a%n
i2, j2 := b/n, b%n
// 尝试向右平移(保持身体水平/垂直状态)
move(i1, j1+1, i2, j2+1)
// 尝试向下平移(保持身体水平/垂直状态)
move(i1+1, j1, i2+1, j2)
// 当前处于水平状态,且 grid[i1 + 1][j2] 无障碍,尝试顺时针旋转90°
if i1 == i2 && i1+1 < n && grid[i1+1][j2] == 0 {
move(i1, j1, i1+1, j1)
}
// 当前处于垂直状态,且 grid[i2][j1 + 1] 无障碍,尝试逆时针旋转90°
if j1 == j2 && j1+1 < n && grid[i2][j1+1] == 0 {
move(i1, j1, i1, j1+1)
}
}
ans++
}
return -1
}function minimumMoves(grid: number[][]): number {
const n = grid.length;
const target: number[] = [n * n - 2, n * n - 1];
const q: number[][] = [[0, 1]];
const vis = Array.from({ length: n * n }, () => Array(2).fill(false));
vis[0][0] = true;
const move = (i1: number, j1: number, i2: number, j2: number) => {
if (i1 >= 0 && i1 < n && j1 >= 0 && j1 < n && i2 >= 0 && i2 < n && j2 >= 0 && j2 < n) {
const a = i1 * n + j1;
const b = i2 * n + j2;
const status = i1 === i2 ? 0 : 1;
if (!vis[a][status] && grid[i1][j1] == 0 && grid[i2][j2] == 0) {
q.push([a, b]);
vis[a][status] = true;
}
}
};
let ans = 0;
while (q.length) {
for (let k = q.length; k; --k) {
const p: number[] = q.shift();
if (p[0] === target[0] && p[1] === target[1]) {
return ans;
}
const [i1, j1] = [~~(p[0] / n), p[0] % n];
const [i2, j2] = [~~(p[1] / n), p[1] % n];
// 尝试向右平移(保持身体水平/垂直状态)
move(i1, j1 + 1, i2, j2 + 1);
// 尝试向下平移(保持身体水平/垂直状态)
move(i1 + 1, j1, i2 + 1, j2);
// 当前处于水平状态,且 grid[i1 + 1][j2] 无障碍,尝试顺时针旋转90°
if (i1 == i2 && i1 + 1 < n && grid[i1 + 1][j2] == 0) {
move(i1, j1, i1 + 1, j1);
}
// 当前处于垂直状态,且 grid[i2][j1 + 1] 无障碍,尝试逆时针旋转90°
if (j1 == j2 && j1 + 1 < n && grid[i2][j1 + 1] == 0) {
move(i1, j1, i1, j1 + 1);
}
}
++ans;
}
return -1;
}/**
* @param {number[][]} grid
* @return {number}
*/
var minimumMoves = function (grid) {
const n = grid.length;
const target = [n * n - 2, n * n - 1];
const q = [[0, 1]];
const vis = Array.from({ length: n * n }, () => Array(2).fill(false));
vis[0][0] = true;
const move = (i1, j1, i2, j2) => {
if (i1 >= 0 && i1 < n && j1 >= 0 && j1 < n && i2 >= 0 && i2 < n && j2 >= 0 && j2 < n) {
const a = i1 * n + j1;
const b = i2 * n + j2;
const status = i1 === i2 ? 0 : 1;
if (!vis[a][status] && grid[i1][j1] == 0 && grid[i2][j2] == 0) {
q.push([a, b]);
vis[a][status] = true;
}
}
};
let ans = 0;
while (q.length) {
for (let k = q.length; k; --k) {
const p = q.shift();
if (p[0] === target[0] && p[1] === target[1]) {
return ans;
}
const [i1, j1] = [~~(p[0] / n), p[0] % n];
const [i2, j2] = [~~(p[1] / n), p[1] % n];
// 尝试向右平移(保持身体水平/垂直状态)
move(i1, j1 + 1, i2, j2 + 1);
// 尝试向下平移(保持身体水平/垂直状态)
move(i1 + 1, j1, i2 + 1, j2);
// 当前处于水平状态,且 grid[i1 + 1][j2] 无障碍,尝试顺时针旋转90°
if (i1 == i2 && i1 + 1 < n && grid[i1 + 1][j2] == 0) {
move(i1, j1, i1 + 1, j1);
}
// 当前处于垂直状态,且 grid[i2][j1 + 1] 无障碍,尝试逆时针旋转90°
if (j1 == j2 && j1 + 1 < n && grid[i2][j1 + 1] == 0) {
move(i1, j1, i1, j1 + 1);
}
}
++ans;
}
return -1;
};