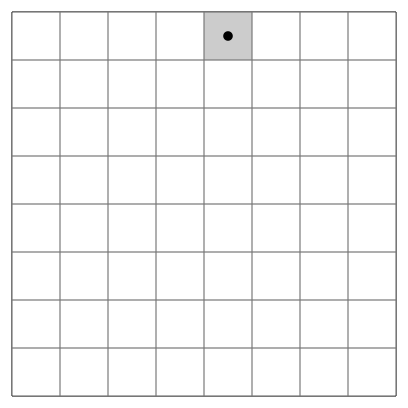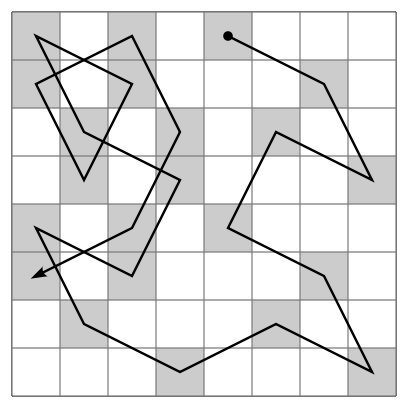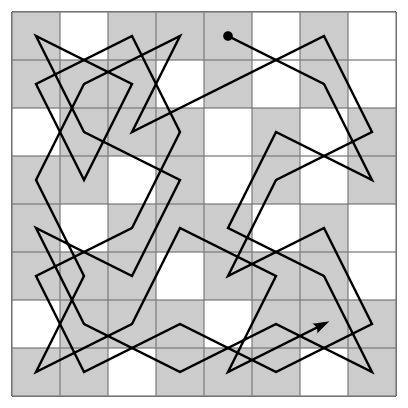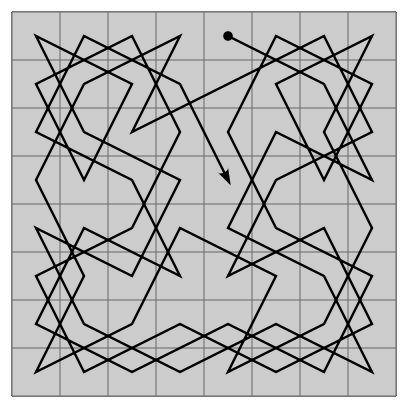
A knights tour is a sequence of L-shaped knight moves on an m by n chessboard such that, following the sequence, a knight visits each square exactly once. If the sequence ends with the knight returning to its starting position, the tour is called closed. The problem of finding a knights tour is an instance of the more general NP-Complete hamiltonian path problem. While the knights tour problem can be solved in linear time, the implementation here uses backtracking and is significantly slower. In this implementation, each of 8 possible moves are tried at each level of the recursive tree. If at any point the algorithm finds a dead end in the sequence of moves it is currently exploring, it undoes the current move and continues to exhaust all moves from the earlier steps. The algorithm continues trying all of these moves in a brute force way until it either reaches a depth of m+n in the recursive tree and has covered squares on the board or has tried all possible moves.