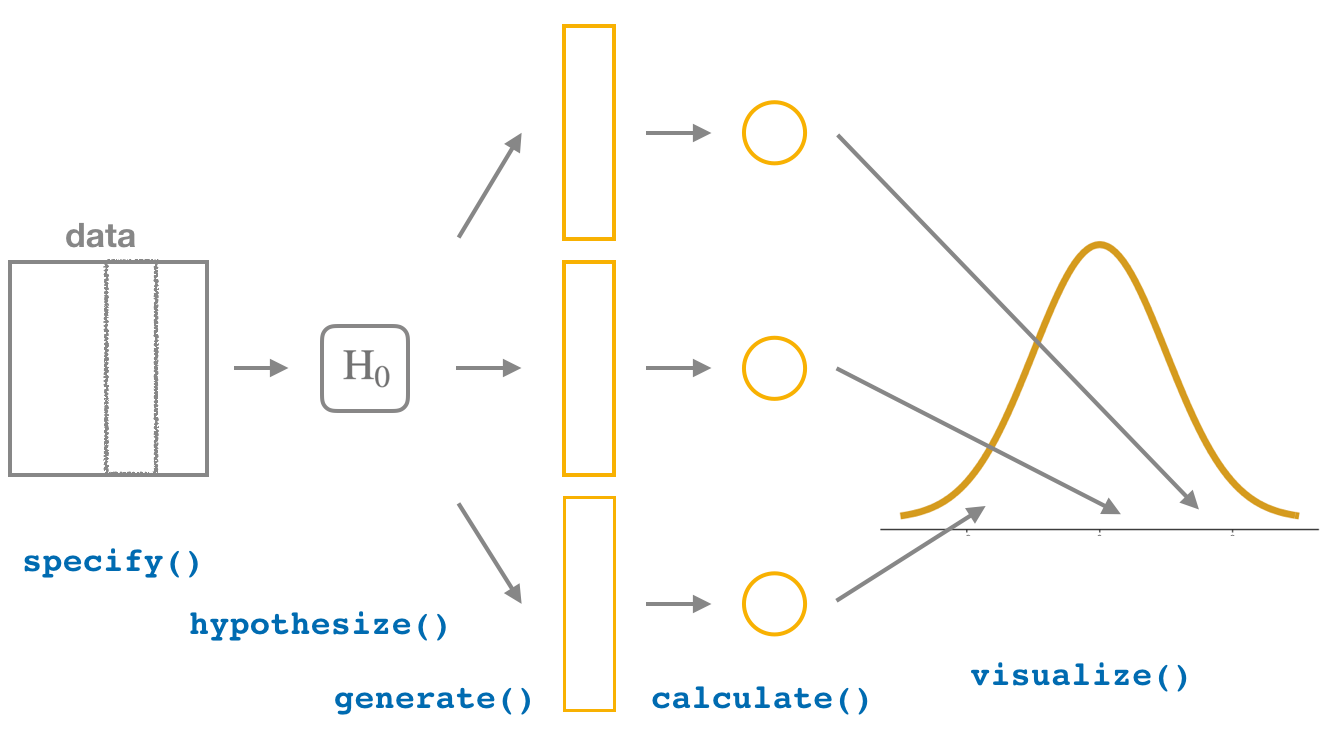
library(tidyverse)
-library(infer)
-set.seed(2)
-
-data <- read_csv("https://moderndive.com/data/ageAtMar.csv")
-
-graduation <- rep_sample_n(data, size = 500, replace = F) %>% ungroup %>% select(-replicate)
-Rows: 5534 Columns: 1 -── Column specification ──────────────────────────────────────────────────────── -Delimiter: "," -dbl (1): age - -ℹ Use `spec()` to retrieve the full column specification for this data. -ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message. --
Reminders¶
-
-
- Worksheet 6 and tutorial 6 are due on Sunday -
- Practice problems for mid-term 1 - Please find under Midterm 1 module on Canvas -
- Midterm 1 is on Thursday July 20 at 1:30 PM in ESB 1012
-
-
- open book (but not collaborative) -
- will be served on Canvas -
- covers all the material from modules 1 - 4 -
- make sure you have either Chrome, Firefox, or some other browser compatible with all of Canvas functionality. Sometimes Safari has trouble loading images and math. -
- Download your previous worksheets/tutorials onto your local computer just in case! Do not try to access online during the exam. -
- ChatGPT is not allowed -
-
Statistical Inference¶
-
-
- Point estimation: we estimate an unknown parameter using a single number calculated from sample data. -
- Interval estimation: we estimate an unknown parameter using an interval of values that plausibly contain the true parameter value (and state how confident we are the interval captures the true value). -
-
-
- Hypothesis testing: we make a statement about the value of an unknown population parameter, and we check whether or not the data obtained from the sample provide evidence against this claim. -
Let's assume that the deck of cards is fair. What assumption are we making about the value of the population proportion of red cards in the deck ($p$)?
-Assume $p$ = 0.5
- -Randomly draw $n = 10$ cards¶
Suppose we find $\hat p$ = 1!
- -Hypothesis Testing Overview¶
-
-
- State hypotheses -
- Set significance level -
- Collect data -
- Calculate test statistic -
- Calculate P-value -
- Draw a conclusion -
Hypothesis testing¶
Suppose Apple claims that the new Macbook Pro can work for more than 20 hours without a recharge. You suspect that the battery life is less than they claim. You randomly selects multiple Macbooks and measures how long they hold up without a recharge. You find the average time is 19 hours. Is there sufficient evidence to refute Apple's claim?
- -
-
-
-Hypotheses¶
In statistics, a hypothesis is a statement about a parameter. We carry out a hypothesis test to test the claim.
--
-
- Null hypothesis ($H_0$) -
- Alternative hypothesis ($H_1$ or $H_A$) -
Null Hypothesis¶
Statement about the value of a population parameter whose general form is:
-$H_0$ : population parameter = specified value
- -E.g. In the Macbook example, we want to test
-$H_0: \mu = 20$ hours
-where $\mu$ is the true mean of the battery life of new Macbook Pros.
- --
-
- The null hypothesis states that an observed difference is due to chance variation -
- Claim that there is "no effect" or "no difference of interest." -
- It often represents the status quo, what you should conclude if there’s no evidence to say otherwise. -
- For example unless we see "strong" evidence that a new, untested drug works, we are going to assume that it does not. -
Alternative Hypothesis¶
Statement that opposes the null hypothesis
-$H_A$ : population parameter $\ne$ specified value
-$H_A$ : population parameter $>$ specified value
-$H_A$ : population parameter $<$ specified value
- -E.g. In the Macbook example, $H_A: \mu <20$ hours (we are testing whether there is evidence to refute Apple's claim)
- --
-
- States that an observed difference is real -
- Often it is a claim the experimenter or researcher wants to find evidence to support -
Hypotheses¶
-
-
- The hypotheses should be formulated before viewing or analyzing the data. -
- We start by assuming the null hypothesis is true, and then we see if the data is compatible or incompatible with this assumption. -
Test statistic¶
-
-
- We start by collecting a sample and calculating the statistic that we are going to use for the test. -
- A test statistic is a point estimate/sample statistic used for hypothesis testing -
- As usual, everything revolves around the distribution of our statistic -
Example¶
Suppose 500 randomly sampled Canadian adults recently completed a survey indicating their age of graduation from school. The ages are stored in the data set graduation. Suppose from past surveys, it is known that the average age of graduation was 23 years. We are interested to see if the average in recent years has increased.
library(tidyverse)
-library(infer)
-
-head(graduation)
-| age |
|---|
| <dbl> |
| 24 |
| 16 |
| 22 |
| 23 |
| 18 |
| 22 |
Do the data suggest that the average age of graduation for Canadian adults has increased in recent years?
- -Q. What is the null and alternative hypotheses?¶
A. $H_0: \mu = 23 \; \;$ vs. $\; \; H_A: \mu \ne 23$
-B. $H_0: \mu = 23 \; \;$ vs. $\; \; H_A: \mu < 23$
-C. $H_0: \mu = 23 \; \;$ vs. $\; \; H_A: \mu > 23$
-where $\mu$ represents the mean age of graduation for all Canadian adults in recent years.
- -Look at the data¶
-observed_sample_mean <- graduation %>% summarize(mean_age = mean(age)) %>% pull()
-observed_sample_mean
-graduation %>% ggplot(aes(x = age)) +
- geom_histogram(binwidth = 3, color = "white") +
- theme(text = element_text(size=20))
-set.seed(2018)
-boot_distn <- graduation %>%
- specify(response = age) %>%
- generate(type = "bootstrap", reps = 1000) %>%
- calculate(stat = "mean") %>%
- visualize() +
- geom_vline(xintercept = observed_sample_mean, color = "red", alpha=.3, lwd=2) +
- xlab("Mean Age") +
- theme(text = element_text(size=20))
-boot_distn
-Idea¶
-
-
- Hypothesis tests assume the null hypothesis is true -
- Bootstrap distribution centered at the observed sample statistic -
-
-
- If the null hypothesis is true then we would expect the mean value of the data to be 23 -
- Let's shift all of the measurements so that the mean of the shifted data is equal to the hypothesized mean -
set.seed(2018)
-null_distn <- graduation %>%
- specify(response = age) %>%
- hypothesize(null = "point", mu = 23) %>%
- generate(reps = 1000) %>%
- calculate(stat = "mean")
-
-head(null_distn)
-Setting `type = "bootstrap"` in `generate()`. - --
| replicate | stat |
|---|---|
| <int> | <dbl> |
| 1 | 22.910 |
| 2 | 23.172 |
| 3 | 22.750 |
| 4 | 22.814 |
| 5 | 23.176 |
| 6 | 22.954 |
null_distn %>% visualize() +
- geom_vline(xintercept = observed_sample_mean, color = "red", lwd=2, alpha=.3) +
- geom_vline(xintercept = 23, color = "blue", lwd=2, alpha=.3) +
- xlab("Mean age") +
- theme(text = element_text(size=20))
-$p$-value¶
-
-
$p$-value summarizes the evidence
-
-It describes how unusual the data would be if $H_0$ were true.
-
-$p$-value is defined as the probability of observing a result as extreme or more extreme towards the alternative hypothesis than what we observed given that $H_0$ is true.
-
-
 -
-
-
-# plot the null model with shaded p-value
-null_model_plot <- null_distn %>%
- visualize() +
- shade_p_value(obs_stat = observed_sample_mean, direction = "greater") +
- geom_vline(xintercept = 23, color = "blue", lwd=2) +
- xlab("Mean age") +
- theme(text = element_text(size=20))
-null_model_plot
-head(null_distn)
-| replicate | stat |
|---|---|
| <int> | <dbl> |
| 1 | 22.910 |
| 2 | 23.172 |
| 3 | 22.750 |
| 4 | 22.814 |
| 5 | 23.176 |
| 6 | 22.954 |
pvalue <- null_distn %>%
- get_pvalue(obs_stat = observed_sample_mean, direction = "greater")
-pvalue
-
-sum(null_distn$stat > observed_sample_mean)/1000
-| p_value |
|---|
| <dbl> |
| 0.01 |
Significance level $\alpha$¶
-
-
The significance level is a predetermined number such that we reject $H_0$ if the $p$-value is less than or equal to that number
-
-In practice, the common significance levels are $\alpha=0.01$, $0.05$ or $0.10$
-
-
-
-
-
- We should choose the significance level ahead of time. -
- When we reject $H_0$, we say the results are statistically significant.
-
-
- If $p$-value $\leq \alpha\; \Rightarrow$ Reject $H_0$ -
- If $p$-value $> \alpha\; \Rightarrow$ Do not reject $H_0$ -
-
Conclusion¶
We estimate the $p$-value to be 0.01.
-Suppose $\alpha = 0.05$, then we reject the null hypothesis. -There is evidence that the true average age of graduation of Canadian adults in recent years is greater than the previously documented value of 23 years.
- -Decisions and Types of errors in Hypothesis Testing¶
 -
-
-
-Type I error¶
-
-
- The probability of committing a type I error equals the significance level you set for your hypothesis test denoted by $\alpha$. -
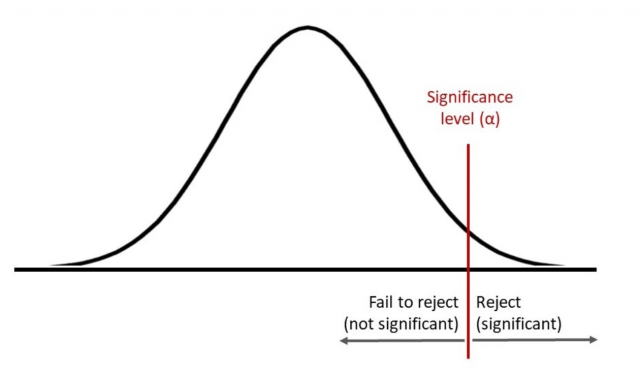
For example, for a right-tailed test with $\alpha = 0.05$:
-Suppose we have a null model below
- -
-
-
--
-
- When our test statistic falls in the rejection region, the $p$-value will be less than the significance level. The null hypothesis is rejected. -
Type II error¶
-
-
- The probability of a Type II Error is denoted by $\beta$ -
- We will talk more about this in future lectures -
Q. In our example, we rejected the null hypothesis. What type of error are we at risk of making?¶
A. Type I error
-B. Type II error
-C. Neither
- -Hypothesis testing summary¶
-
-
- State hypotheses -
- Set significance level -
- Collect data -
- Calculate test statistic -
- Calculate P-value -
- Draw a conclusion -
Get started on worksheet 6!¶
-
-
- Navigate to Canvas, open
worksheet_06
-
If you get stuck:
--
-
- Discuss with your neighbours, the TAs & Instructors, and consult the textbook reading to help you get unstuck when needed! -
- Ask your group mates if you need help with any questions -
- The TAs and myself will walk around and answer questions -
What did you learn today?¶
-
-
-
-
-
Take a break!¶
Come back at 3:06 PM and Parsa will lead you through tutorial_06
 -
-
-
-