- 纹理是什么:一种可供着色器读写的结构化存储形式 Image[Height][Width][4]
- 为什么出现了纹理:
- 通过牺牲几何细节,减低了建模工作量,减低了模型数据储存空间,同时也提升了读取速度。能够高效修改表面材质和模型。[Texturing is a technique for efficiently modeling variations in a surface’s material and finish.]
- 纹理管线:
模型空间位置=>投影函数[展uv阶段用到的:平面映射,圆柱映射,立方体映射]
=>纹理映射=>纹理坐标=>通讯函数[Wrap,Repeat,Mirror,Clamp,Border,Offset,Tilling]=>纹理空间坐标=>
纹理采样[避免依赖纹理读取][SAMPLER:Uniform类型的变量]=>纹理值
- 依赖纹理读取:在RTR4中的原文解释是1
- 纹素:图像纹理上的像素通常被称为纹素,以区分它和屏幕上的像素。2
- 纹理管线:纹理化的过程广义上被描述成为纹理化管线。3
- 纹理管线的过程:纹理化的始点一般是模型上的局部坐标,也可以是世界坐标。以达到模型移动之后,纹理也跟着移动的目的。使用投影函数(projector function),获取到的坐标叫做纹理坐标(texture coordinates),投影函数被用作于获取纹理。这一过程叫做映射(Mapping)。有的时候用作纹理的图像就被叫做为纹理,这其实是不太严谨的。
在使用刚刚获取的纹理坐标来获取纹理之前,还会使用一个或多个通讯函数(corresponder functions)来将纹理坐标转换到纹理空间(Texture Space location)。纹理空间的坐标将会从纹理获取对应的值(Obtain value),而获取到的值还可以是数组的索引值来检索另外一张图像纹理的像素,会被进一步被潜在地被转换(value transform function),最后获取到的数值被用作于修改模型表面的某种属性。4
- 例子:一面砖墙的例子 模型空间坐标(x,y,z)为(-2.3,7.1,88.2)---Object space location 使用投影函数[projector Function]将三维坐标(x,y,z)转换成二维坐标(u,v) 假设投影得到的UV坐标为(0.32,0.29),这个纹理坐标将会用于查找图像上的颜色---parameter space coordinates 假设纹理分辨率为256*256,所以在通信函数[Corresponder Function]中将返回实际图像中坐标位置(0.32,0.29) * (256,256)=(81.92,74.24)。---texture space location 去掉分数后,像素(81,74)就在图像上会被寻获[Obtain Value],得到颜色值(0.9,0.8,0.7)。---texture value 由于纹理的颜色空间是SRGB,想用于着色计算就必须转换成Linear空间[Value Transform Function],最后转换为(0.787,0.604,0.448)---transformed texture value 注:本例使用的投影方式相当于正交投影,砖墙其表面的一个值经过这个投影方式返回[0,1]的UV值
- API裁剪纹理 使得只有裁剪过后的子图像运用到后续着色中
- 矩阵变换[适用于顶点着色器或片元着色器] 常见变换有: Translating,Rotating,Scaling,Shearing(剪切) 需要注意的是:纹理图像本身没有发生变化,是纹理坐标空间发生了变化。5
- 包裹/寻址模式 Wrap Mode/Texture Addressing Mode
- Wrap,Repeat/Tile
- Mirror
- Clamp/Clamp to edge
- Border/Clamp to border
纹理值一般包括:
- 图像纹理 Image Texturing
- 程序纹理 Procedural Texturing
- Rapidly sample
-
Filter Textured images
[解决纹理映射在模型表面后,经过旋转,缩放之后一个像素可能覆盖多个纹素的情况]
-
Magnification 放大插值方式
- 解决少数几个纹素覆盖多个像素
- Nearest neighbor filtering 最邻近点插值滤波[常用于制作像素化风格(pixelation)] 像素化的产生原因是:当放大的时候,像素当前的值直接取离像素中心最近的纹素。
-
Bilinear filtering 双线性插值滤波(使用2*2的滤波器)
- 双线性插值举例: 假设取得点P(u,v)=(81.92,74.24) 从样本位置减去像素中心-(0.5,0.5)=(81.42,73.74) 最接近样本位置的四个像素点范围是t(x,y)=(81,73),t(x+1,y+1)=(82,74) 样本中心相对于该四个像素中心形成的坐标系的位置是(0.42,0.74) 所以插值颜色= $(1-0.42)(1-0.74)t(x,y)+$ $0.42(1-0.74)t(x+1,y)+$ $(1-0.42)0.74t(x,y+1)+$ $0.420.74t(x+1,y+1)$ 四个纹素的权重值之和为1
-
Cubic filtering 三次卷积插值滤波/立方卷积插值 (使用4 * 4或者5 * 5滤波器)
卷积采样公式:
$F(i+v,j+u)=\sum_{row=-1}^{2}\sum_{col=-1}^{2}f(i+row,j+col)S(row-v)S(col-u)$
$S(x)=\left{\begin{matrix} (a+2)|x|^3-(a+3)|x|^2+1 & |x|\leq1\ a|x|^3-5a|x|^2+8a|x|-4a & 1<|x|<2\ 0&其他 \end{matrix}\right.$
- 立方卷积插值举例: 假设取得点P(u,v)=(81.92,74.24) 向下取整取最邻近的像素点作为原点P00=(81,74),u=0.92,v=0.24 计算取样原点P00周围其他15个纹素的S(row-v)*S(col-u)的值 最后卷积求得采样结果
-
Qu´ılez光滑曲线插值:
- 主要思路:使用光滑的曲线在2*2的纹素组之间进行插值
- 常见的插值曲线:
- smoothstep:$x^3(3-2x)$
- quintic:$x^3(6x^2-15x+10)$
- 采样例子: 假设取得点P=(81.92,74.24) u'=81.92 * 256+0.5=20972.02,v'=74.24 * 256+0.5=19005.94[+0.5:保证在插值曲线上x=0,s(x)=0.5,从而固定曲线的位置在(0,0.5); 256*:使得frac取小数曲线在0~1之间出现256个y≈1的点保证在纹理像素点数量和当前曲线的频率相匹配] u'=0.02,v'=0.94 u'=(s(u')-0.5+20972)/256[/256:Remap回(0,256);-0.5偏移(0,0.5)到(0,0)] v'=(s(v')-0.5+19005)/256 然后再用双线性插值的办法进行插值 参考Graphtoy曲线:6
- 插值效果对比: 最邻近<线性<Qu´ılez曲线插值<立方卷积插值
-
Minnification 缩小插值方式
- 解决多个纹素覆盖一个像素,造成纹素跨度过大导致颜色丢失与闪烁
- 为了保障采样质量,需要确保纹理的信号频率不大于采样频率的一半,即每个纹素至少对应一个像素,所以要么提高采样频率,要么降低纹理的频率。
- 提高采样频率:
-
Nearest neighbor filtering 最邻近点插值滤波
- 原理与放大插值一样,由于一个像素映射时覆盖了多个纹素导致出现伪影(artifacts) 这样的伪影会根据观察者的视角的移动而发生变化,属于时效性的走样。
-
Bilinear filtering 最邻近点插值滤波
- 原理与放大插值一样,但是如果一个像素映射是覆盖了超过4个纹素的时候,就又会产生走样现象
-
Nearest neighbor filtering 最邻近点插值滤波
- 降低纹理的频率:
- 纹理走样处理思路:都是通过预处理纹理创建出一组纹素对应一个像素快速近似的数据结构。
- MipMapping
- 处理过程:原始纹理被反复使用滤波器降采样成更小的图像,直到纹理的一个维度或者两个维度都等于一个纹素大小。
- 高质量的Mipmap两大要素:
- Good Filtering
- box filter
- 2*2的均值filter,质量差,存在会模糊低频的问题。
- 好的Filter有:高斯,Lanczos,Kaiser类似的Filter,有一些API本身就支持效果比较好的Filter内置在GPU中
- box filter
- Gamma correction 由于大部分的纹理贴图储存空间是非线性空间(SRGB?),不进行Gamma矫正会导致使用完滤波器之后,会修改Mipmap的感知亮度。不使用Gamma矫正,当离物体得越远,物体整体会变得更加得暗,对比度和细节也会受到影响。所以使用SRGB纹理的时候,参与着色之前,必须将其转换成Linear空间
- Good Filtering
- 访问使用Mipmap,计算LOD(Level of Detail)
- 利用像素单元形成的四边形中,较长的边缘来近似像素的覆盖范围
- 另一种是最常用的,测量四个导数的绝对值的最大值作为测量值(
$\frac{\partial u}{\partial x},\frac{\partial v}{\partial x},\frac{\partial u}{\partial y},\frac{\partial v}{\partial y}$ )- float mipmapLevel(float2 uv) {
float dx = ddx(uv);//dudv/dx
float dy = ddy(uv);//dudv/dy
float d = max(dot(dx, dx), dot(dy, dy)); return 0.5 * log2(d); //log2(sqrt(d))小于等于0则说明d<=1则texel小于等于pixel需要放大纹理插值 //大于0这说明需要使用缩小滤波后的Mipmap //Log2是由于缩小滤波的层级一共有Log2(max(Width,Height)) } - DDX,DDY需要注意: 由于它是基于相邻像素的梯度来计算的,所以只能在FragmentShader中使用,而不能用在VertexShader,要想在VS中使用Mipmap,需要手动计算LOD
- 三线性插值 (u,v,d)三元组获取Mipmap d是float类型,采样每个像素时,对d最近的两层Level做一次双线性过滤,整个过程叫做三线性插值。
- float mipmapLevel(float2 uv) {
- 内存消耗:比原本多了1/3
- 存在问题:过度模糊[overblurring],由于假设贴图投射到屏幕空间时都是各向同性的,但实际运用过程中,纹理空间中UV的跨度是不均匀的,是各向异性的。访问MipMap的时候检索的是正方形区域,检索矩形区域是不可能的,为了避免走样,我们选择最大跨度的方向作为正方形边长,这就通常导致采样的纹素在UV方向上跨度不一致的时候,跨度小的方向采样到的LOD偏大(模糊)[即max(dot(dx, dx), dot(dy, dy));]
- Anisotropic Filtering 各向异性过滤方法:
-
RipMap
- 预处理不光生成正方形区域,也生成了各种比例的矩形区域
- 缺点:部分解决UV跨度局限在正方形区域问题,但是实际上还是使用了一个矩形来近似采样,有的时候在斜向对角的情况拿一个矩形去框住采样区域也是不太合适的,也包含了太多无关紧要的采样区域,这样得出来的采样结果也是会存在一定的过度模糊的效应。
-
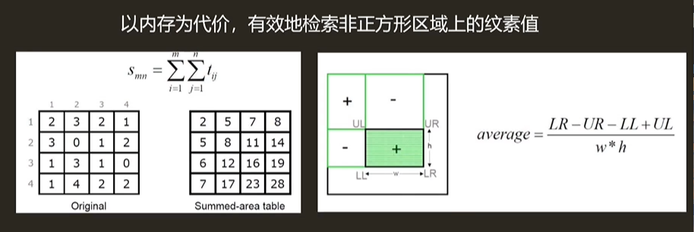
Summed Area Table 积分图
- 使用SAT之前,首先得创建一个与纹理大小相同的数组,数组的每个位置需要计算当前这个位置和原点(0,0)形成的矩形中所有纹素之和。
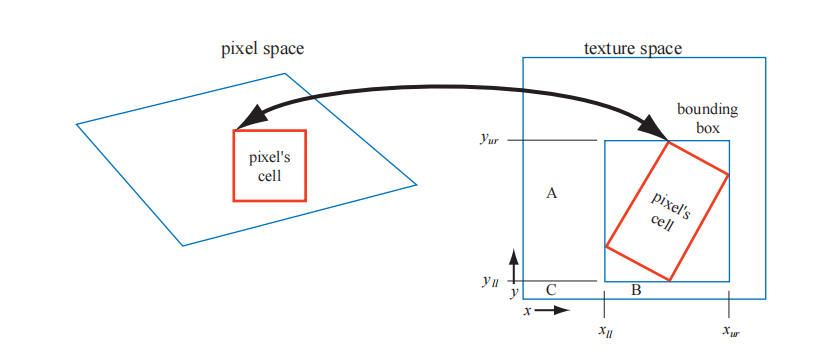
- 在纹理化的过程中,像素单元投影回纹理被矩形绑定,然后访问SAT求和区域以计算矩形的平均颜色,平均值计算公式如下:
D3D:注意坐标原点为左上
示例: 求(4,4)到(2,3)矩形区域 C=(28+5-8-17)/(3*2)=4/3=(1+2+1+0+2+2)/(3 *2) 注意:(1,2)为包围盒的左上角 OpenGL:RTR4配图 注意坐标原点为左下
$c=\frac{ s[x_{ur},y_{ur}]-s[x_{ur},y_{ll}]-s[x_{ll},y_{ur}]+s[x_{ll},y_{ll}] }{ (x_{ur}-x_{ll})(y_{ur}-y_{ll}) }$ 注意:$(x_{ll}+1,y_{ll}+1)$为包围盒的左下角- 缺点:跟RipMap类似,也是由于在对角线视角,存在像素投影到纹理空间的矩形区域是斜着的,存在有无关紧要的采样区域,从而造成一定的模糊效应。耗费内存多,额外需要至少2倍的内存开销,更大的纹理也需要更高的精度。
- 优点:在各向异性过滤的方法中速度算是比较快的。
-
Unconstrained Anisotropic Filtering 无约束各向异性过滤
- 原理:重用现有的Mipmap硬件,在将像素投影回纹理空间后,在投影形成的四边形区域中,使用最短的边作为d决定LOD,使得Mipmap样本的平均面积变小(减少模糊),然后创建平行于四边形的最长边并且穿过中心的各向异性线。当各向异性过滤的数值在1:1到2:1[指各向异性数值2X,4X,8X,16X,具体采样的时候应该是各向异性过滤线跟d的比值?]之间时,沿着这条线采集两个样本。在各向异性过滤数值较高的情况下沿轴取的采样点就越多。
- 内存影响不大,开启之后不会消耗3倍的纹理缓存,只会多1/3的缓存消耗
- 采样次数增加,各向异性过滤基于三线性过滤的,当uv不是1:1时,各向异性过滤就会比三线性插值采样更多的点,[16X各向异性过滤采样不一定采样采够128次,需要采样精度到了的时候才会采够128次]
-
EWA过滤
- 原理:不使用矩形区域覆盖投影形成的四边形区域,而是使用椭圆形逐步扩大,使得椭圆能够恰好包裹住四边形区域,减少不必要的采样区域。
-
-
Magnification 放大插值方式
-
Texture coordinate systems differences in DirectX and OpenGL
- DirectX the Upper Left corner[左上角] of texture is (0,0),and the lower right is (1,1)
- OpenGL the texel (0,0) is located in the lower left[左下角],a y-axis-flip from DirectX.
- 浮点型纹理坐标空间像素的中心
- Truncating 截断 DirectX 10 向OpenGL靠拢,中心改为(0.5,0.5),使用向下取整
- Rounding 四舍五入 DirectX 9.0 定义中心为(0,0)
- 纹理大小 纹理图像应用在GPU上通常是POT(power-of-two)2的整数次幂贴图。现代的GPU能够处理任意大小的非2的整数次幂大小的贴图了NPOT(non-power-of-two),但是仍有部分老旧的移动GPU是不支持对NPOT纹理进行mipmapping处理的。现在DX12最大支持16384^2大小的纹素。
- 优化
- CPU提交命令优化
- 纹理图集,纹理数组 通过打包纹理到一起,降低反复纹理传输指令到命令缓冲区的次数,减少因为频繁改变纹理所带来的消耗。
- GPU降低带宽优化
- 压缩纹理 通过硬件解码,减少包体大小,内存使用率提升
- CPU提交命令优化
- 常见的纹理
- CubeMap立方体贴图
- 常用于HDR,LightProbe
- Bump Map
- 不增加顶点的情况下,改变几何体表面的法线,定义出一个虚拟的高度,模拟凹凸不平的效果
- Displacement Map
- 位移贴图是把顶点作位置的移动,需要模型的点比较多。可以使用动态曲面细分的技巧,减少所需的顶点。
- CubeMap立方体贴图
Footnotes
-
One term worth explaining at this point is dependent texture read, which has two definitions. The first applies to mobile devices in particular.When accessing a texture via texture2D or similar, a dependent texture read occurs whenever the pixel shader calculates texture coordinates instead of using the unmodified texture coordinates passed in from the vertex shader [66]. Note that this means any change at all to the incoming texture coordinates, even such simple actions as swapping the u and v values. Older mobile GPUs, those that do not support OpenGL ES 3.0, run more efficiently when the shader has no dependent texture reads, as the texel data can then be prefetched. The other, older, definition of this term was particularly important for early desktop GPUs. In this context a dependent texture read occurs when one texture’s coordinates are dependent on the result of some previous texture’s values. For example, one texture might change the shading normal, which in turn changes the coordinates used to access a cube map. Such functionality was limited or even non-existent on early GPUs. Today such reads can have an impact on performance, depending on the number of pixels being computed in a batch, among other factors.See Section 23.8 for more information. 机翻:在这一点上值得解释的一个术语是依赖纹理读取,它有两个定义。 第一种特别适用于移动设备。 当通过texture2D或类似的方法访问纹理时,每当像素着色器计算纹理坐标时,就会发生一个相关的纹理读取,而不是使用从顶点着色器[66]传入的未修改的纹理坐标。 请注意,这意味着对传入纹理坐标的任何更改,即使是交换u和v值这样的简单操作。 旧的移动GPU,那些不支持OpenGLES3.0的,当着色器没有依赖的纹理读取时,运行效率更高,因为文本数据可以被预取。对于早期的桌面GPU来说,这个术语的另一个更古老的定义尤为重要。 在此上下文中,当一个纹理的坐标依赖于某些先前纹理的值的结果时,就会发生依赖的纹理读取。 例如,一个纹理可能会改变着色法线,从而又会改变用于访问立方体映射的坐标。这些功能在早期的GPU上是有限的,甚至是不存在的。今天,这种读取可以影响性能,这取决于在批处理中计算的像素数,以及其他因素。 详情见第23.8节。 ↩
-
The pixels in the image texture are often called texels, to differentiate them from the pixels on the screen. ↩
-
Texturing can be described by a generalized texture pipeline. ↩
-
A location in space is the starting point for the texturing process. This location can be in world space, but is more often in the model’s frame of reference, so that as the model moves, the texture moves along with it. Using Kershaw’s terminology [884], this point in space then has a projector function applied to it to obtain a set of numbers, called texture coordinates, that will be used for accessing the texture. This process is called mapping, which leads to the phrase texture mapping. Sometimes the texture image itself is called the texture map, though this is not strictly correct. Before these new values may be used to access the texture, one or more corresponder functions can be used to transform the texture coordinates to texture space. These texture-space locations are used to obtain values from the texture, e.g., they may be array indices into an image texture to retrieve a pixel. The retrieved values are then potentially transformed yet again by a value transform function, and finally these new values are used to modify some property of the surface, such as the material or shading normal. Figure 6.2 shows this process in detail for the application of a single texture. The reason for the complexity of the pipeline is that each step provides the user with a useful control. It should be noted that not all steps need to be activated at all times. ↩
-
This is because texture transforms actually affect the space that determines where the image is seen. The image itself is not an object being transformed; the space defining the image’s location is being changed. ↩
-
https://graphtoy.com/?f1(x,t)=x&v1=true&f2(x,t)=frac(2*f1(x,t)+0.5)&v2=false&f3(x,t)=trunc(2*f1(x,t)+0.5)&v3=false&f4(x,t)=f2(x,t)%C2%B3*(6*f2(x,t)%C2%B2-15*f2(x,t)+10)&v4=true&f5(x,t)=(f4(x,t)-0.5+f3(x,t))/2&v5=true&f6(x,t)=(f4(x,t))/2&v6=true&grid=true&coords=-0.1721714803184537,0.23028612085331285,1.6334672766021194 ↩