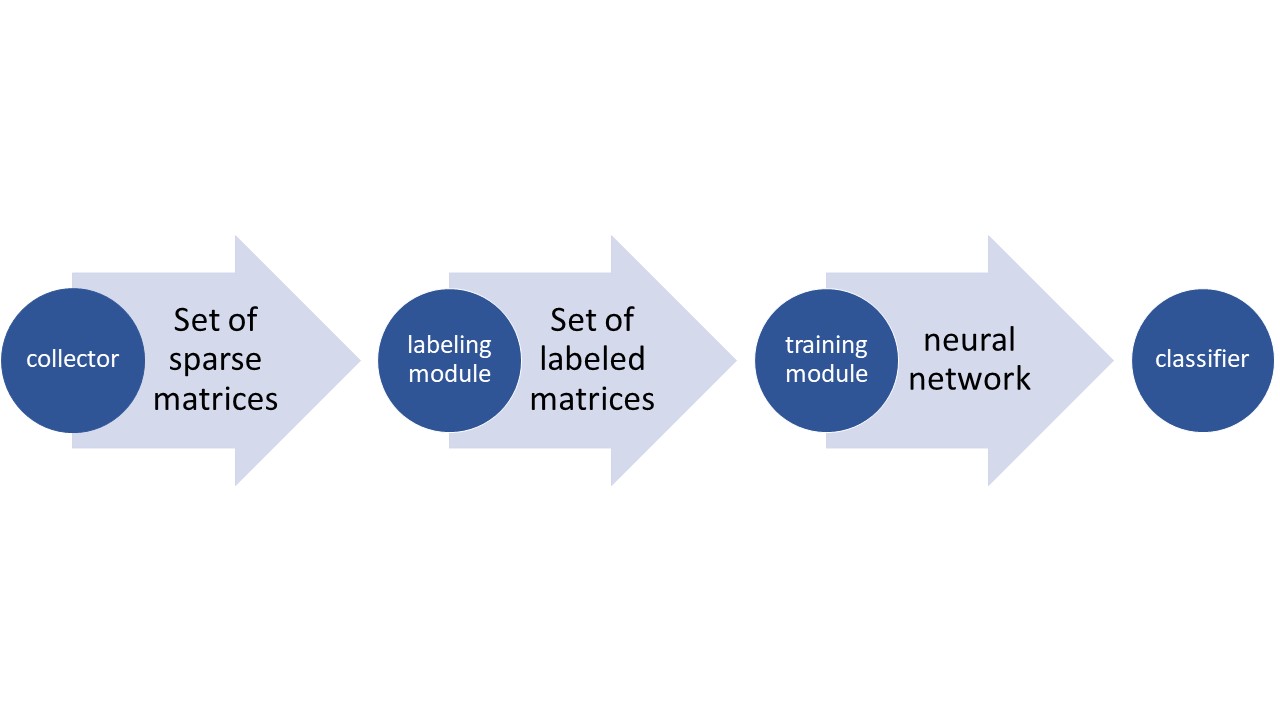
Linear Algebra meets Machine Learning is PSE Project from the Karlsruhe Institute of Technology. It uses a Convolutional Neural Network to find the fastest iterative solver for a given sparse linear system. A part of our program relies on the C++ library ginkgo and the ssget tool.
Finding the solution of a sparse linear system is frequently occurring problem in physics, electrical engineering and other domains of science. When the linear systems get big enough it can take quite a while to solve them. This is why in big sparse linear systems iterative solvers are used to approximate a solution. There are different iterative solvers (our work includes Cgs, Cg, Fcg, Bicgstab and Fcg) which solve different linear systems at different speeds. We trained a neural network to identify which iterative solver solves a given linear system the fastest. You can now give our program a sparse matrix(from the linear system) in the hdf5 format and it will determine which solver will likely solve it the fastest.
If you just want to classify a matrix you can simply clone our repo and start the program on your Linux or Windows device.
git clone https://github.com/TheSlimvReal/PSE---LA-meets-MLIf you however want to access our other functionality (including collecting, labeling and training, explained below) you will have to execute the program on a Linux device. Furthermore you will have to install a c++ compiler and cuda as well as the Ginkgo library (https://github.com/ginkgo-project/ginkgo) and ssget (https://github.com/ginkgo-project/ssget). The paths all of those programs have to be specified in our configuration file.
Our main component is the classifier. Simply start our program by running run.py and insert
classify -p <path> -n <network> In the python shell. The path in this case is the full path to an hdf5 file, containing one matrix. You may specify to use your own neural network but this is not required. The result will be for example:
Matrix 1, predicted solver CgsIf you want to collect your own matrices from the suite sparse collection, type
collect collect -a <amount> -n <name> -s <size> -p <saving_path>Where amount is an integer which specifies how many matrices you want to collect, size is an integer specifying the size of the marices, name is a string specifing the name under which the matrices will be safed and saving_path a full path in which the matrices should be stored(may be an empty string, in which case a default value will be used)
As a result the matrices will be saved in one hdf5 file at the specified path.
If you want to label a set of matrices with their corresponding fastest iterative solver, you may use the command
label -p <path> -n <name> -s <saving path>Where path is a full path specifying which matrices to label(should be an hdf5 file), the saving_path specifies where to safe the matrices with its corresponding labels and the name is s string specifying how the saved hdf5 file should be named. All parameters may be an empty string in which case default values will be used.
If you want to train the neural network yourself you may type
train -p <path> -n <name> -s <saving path>Where path is a full path specifying where the neural network which should be trained i , the saving_path specifies where to safe neural network and the name is s string specifying how the neural network should be named.All of the arguments may be an empty string in which case default values will be used.
Moreover you may type
helpto see all the available commands. Or you may type
<command> --helpfor further information on a specific command.
For furher information please be free to visit our Wiki.
Pull requests are welcome. For major changes, please open an issue first to discuss what you would like to change.
This Project was created by Anna Ricker, Simon Hanselmann, Yannick Funk, Fabian Koffer and Dennis Groetzinger
with the help and overseeing of the supervisors Hartwig Anzt and Markus Goetz.