576. Out of Boundary Paths

576. Out of Boundary Paths (Medium)

There is an m by n grid with a ball. Given the start coordinate (i,j) of the ball, you can move the ball to adjacent cell or cross the grid boundary in four directions (up, down, left, right). However, you can at most move N times. Find out the number of paths to move the ball out of grid boundary. The answer may be very large, return it after mod 10⁹ + 7.

 

Example 1:

Input: m = 2, n = 2, N = 2, i = 0, j = 0
Output: 6
Explanation: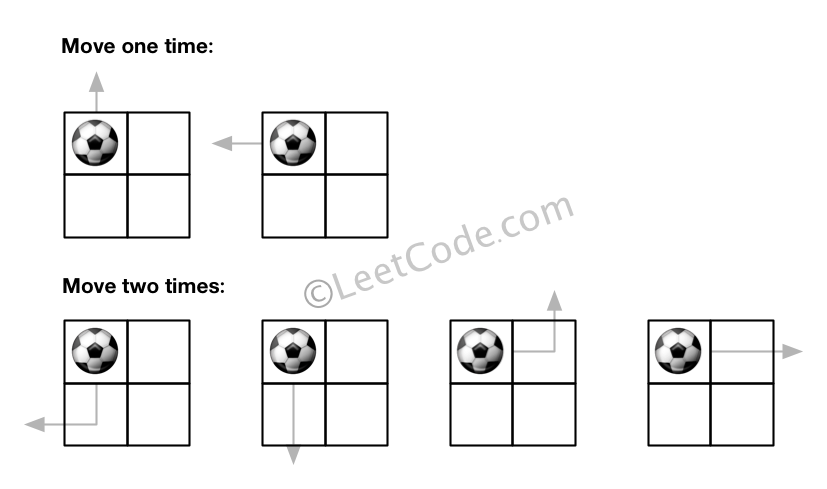

Example 2:

Input: m = 1, n = 3, N = 3, i = 0, j = 1
Output: 12
Explanation: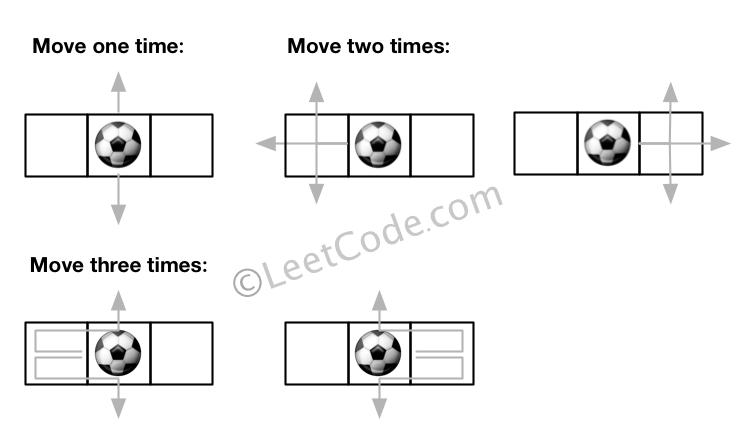

 

Note:

1. Once you move the ball out of boundary, you cannot move it back.
2. The length and height of the grid is in range [1,50].
3. N is in range [0,50].

Related Topics:
Dynamic Programming, Depth-first Search

Similar Questions:

• Knight Probability in Chessboard (Medium)

Solution 1. DP Top-down

// OJ: https://leetcode.com/problems/out-of-boundary-paths/
// Author: github.com/lzl124631x
// Time: O(mnN)
// Space: O(mnN)
typedef long long LL;
class Solution {
    const int dirs[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
    const int mod = 1e9 + 7;
    inline int hash(int x, int y, int n) { return 10000 * x + 100 * y + n; }
    unordered_map<int, int> dp;
    int dfs(int m, int n, int N, int i, int j) {
        if (i < 0 || i >= m || j < 0 || j >= n) return 1;
        if (!N) return 0;
        int key = hash(i, j, N);
        if (dp.count(key)) return dp[key];
        LL cnt = 0;
        for (auto &dir : dirs) cnt = (cnt + dfs(m, n, N - 1, i + dir[0], j + dir[1])) % mod;
        return dp[key] = cnt;
    }
public:
    int findPaths(int m, int n, int N, int i, int j) {
        return dfs(m, n, N, i, j);
    }
};

Solution 2. DP Bottom-up

Let dp[i][j][k] be the number of ways to go out of boundary from point (i, j) using exactly k steps.

dp[i][j][1] is the number of edges the point (i, j) touches.

dp[i][j][k] = Sum( dp[a][b][k - 1] | (a, b) is neighbor of (i, j) )

The answer is Sum( dp[x][y][k] | k = 1, 2, ..., N ).

Follow-up: Why not define dp[i][j][k] as the number of ways to go out of boundary from point (i, j) in k steps?

Because when computing dp[i][j][k], assume we know dp[i][j][k - 1], then we need to compute the ways to go out of boundary with exact k steps.

So we need the number of ways with exact k steps any way.

// OJ: https://leetcode.com/problems/out-of-boundary-paths/
// Author: github.com/lzl124631x
// Time: O(mnN)
// Space: O(mn)
class Solution {
public:
    const int dirs[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
    const int mod = 1e9 + 7;
    int findPaths(int m, int n, int N, int x, int y) {
        if (!N) return 0;
        vector<vector<vector<int>>> dp(m, vector<vector<int>>(n, vector<int>(2)));
        for (int i = 0; i < m; ++i) dp[i][0][1]++, dp[i][n - 1][1]++;
        for (int i = 0; i < n; ++i) dp[0][i][1]++, dp[m - 1][i][1]++;
        int ans = dp[x][y][1];
        for (int k = 2; k <= N; ++k) {
            for (int i = 0; i < m; ++i) {
                for (int j = 0; j < n; ++j) {
                    int val = 0;
                    for (auto &dir : dirs) {
                        int a = i + dir[0], b = j + dir[1];
                        if (a < 0 || a >= m || b < 0 || b >= n) continue;
                        val = (val + dp[a][b][(k - 1) % 2]) % mod;
                    }
                    dp[i][j][k % 2] = val;
                    if (x == i && y == j) ans = (ans + val) % mod;
                }
            }
        }
        return ans;
    }
};

Solution 3. DP Bottom-up

Let dp[i][j][k] be the number of ways to reach point (i, j) from starting point (x, y) with exactly k - 1 steps.

So dp[x][y][1] = 1.

dp[i][j][k] = Sum( dp[a][b][k - 1] | (a, b) is neighbor of (i, j))

dp[i][j][k] should be count into answer if point (i, j) is at the boundary.

// OJ: https://leetcode.com/problems/out-of-boundary-paths/
// Author: github.com/lzl124631x
// Time: O(mnN)
// Space: O(mn)
// Ref: https://leetcode.com/problems/out-of-boundary-paths/solution/
class Solution {
    const int dirs[4][2] = {{0, 1}, {0, -1}, {-1, 0}, {1, 0}};
    const int mod = 1e9 + 7;
public:
    int findPaths(int m, int n, int N, int x, int y) {
        if (!N) return 0;
        vector<vector<vector<int>>> dp(m, vector<vector<int>>(n, vector<int>(2)));
        dp[x][y][1] = 1;
        int ans = 0;
        for (int k = 1; k <= N; ++k) {
            for (int i = 0; i < m; ++i) {
                for (int j = 0; j < n; ++j) {
                    int val = dp[i][j][k % 2];
                    if (!i) ans = (ans + val) % mod;
                    if (i == m - 1) ans = (ans + val) % mod;
                    if (!j) ans = (ans + val) % mod;
                    if (j == n - 1) ans = (ans + val) % mod;
                    val = 0;
                    for (auto &dir : dirs) {
                        int a = i + dir[0], b = j + dir[1];
                        if (a < 0 || a >= m || b < 0 || b >= n) continue;
                        val = (val + dp[a][b][k % 2]) % mod;
                    }
                    dp[i][j][(k + 1) % 2] = val;
                }
            }
        }
        return ans; 
    }
};