A binary tree is named Even-Odd if it meets the following conditions:
- The root of the binary tree is at level index
0, its children are at level index1, their children are at level index2, etc. - For every even-indexed level, all nodes at the level have odd integer values in strictly increasing order (from left to right).
- For every odd-indexed level, all nodes at the level have even integer values in strictly decreasing order (from left to right).
Given the root of a binary tree, return true if the binary tree is Even-Odd, otherwise return false.
Example 1:
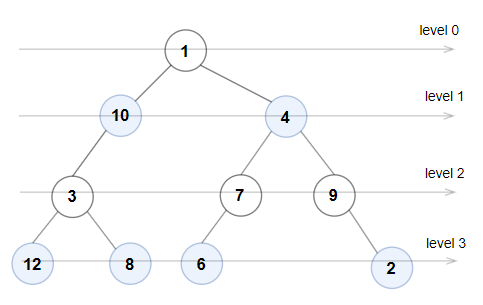
Input: root = [1,10,4,3,null,7,9,12,8,6,null,null,2] Output: true Explanation: The node values on each level are: Level 0: [1] Level 1: [10,4] Level 2: [3,7,9] Level 3: [12,8,6,2] Since levels 0 and 2 are all odd and increasing, and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.
Example 2:
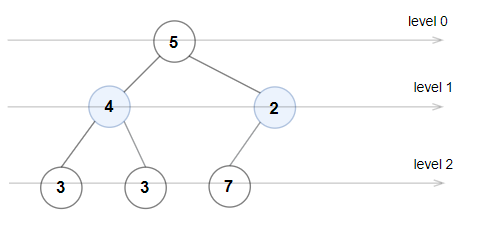
Input: root = [5,4,2,3,3,7] Output: false Explanation: The node values on each level are: Level 0: [5] Level 1: [4,2] Level 2: [3,3,7] Node values in the level 2 must be in strictly increasing order, so the tree is not Even-Odd.
Example 3:
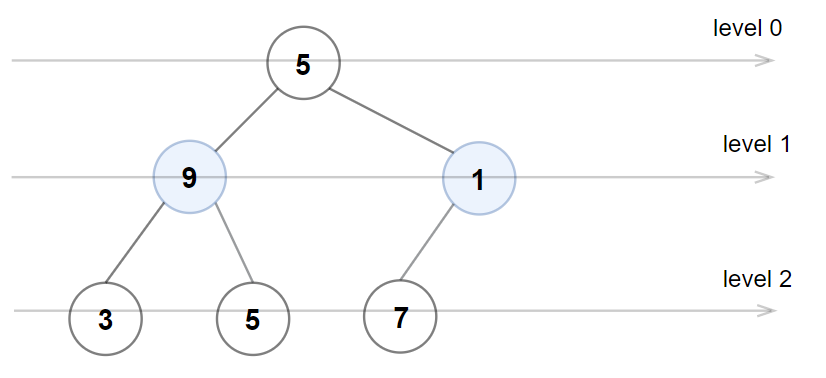
Input: root = [5,9,1,3,5,7] Output: false Explanation: Node values in the level 1 should be even integers.
Example 4:
Input: root = [1] Output: true
Example 5:
Input: root = [11,8,6,1,3,9,11,30,20,18,16,12,10,4,2,17] Output: true
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 106
Related Topics:
Tree
// OJ: https://leetcode.com/problems/even-odd-tree/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
class Solution {
public:
bool isEvenOddTree(TreeNode* root) {
queue<TreeNode*> q;
q.push(root);
int lv = 0;
while (q.size()) {
int cnt = q.size(), prev = lv % 2 == 0 ? 0 : INT_MAX;
while (cnt--) {
auto node = q.front();
q.pop();
if (lv % 2 == 0) {
if (node->val % 2 == 0 || node->val <= prev) return false;
} else {
if (node->val % 2 || node->val >= prev) return false;
}
prev = node->val;
if (node->left) q.push(node->left);
if (node->right) q.push(node->right);
}
++lv;
}
return true;
}
};