Given the integer n representing the number of courses at some university labeled from 1 to n, and the array dependencies where dependencies[i] = [xi, yi] represents a prerequisite relationship, that is, the course xi must be taken before the course yi. Also, you are given the integer k.
In one semester you can take at most k courses as long as you have taken all the prerequisites for the courses you are taking.
Return the minimum number of semesters to take all courses. It is guaranteed that you can take all courses in some way.
Example 1:
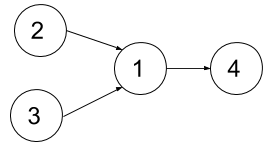
Input: n = 4, dependencies = [[2,1],[3,1],[1,4]], k = 2 Output: 3 Explanation: The figure above represents the given graph. In this case we can take courses 2 and 3 in the first semester, then take course 1 in the second semester and finally take course 4 in the third semester.
Example 2:
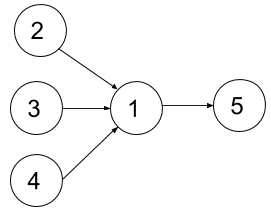
Input: n = 5, dependencies = [[2,1],[3,1],[4,1],[1,5]], k = 2 Output: 4 Explanation: The figure above represents the given graph. In this case one optimal way to take all courses is: take courses 2 and 3 in the first semester and take course 4 in the second semester, then take course 1 in the third semester and finally take course 5 in the fourth semester.
Example 3:
Input: n = 11, dependencies = [], k = 2 Output: 6
Constraints:
1 <= n <= 151 <= k <= n0 <= dependencies.length <= n * (n-1) / 2dependencies[i].length == 21 <= xi, yi <= nxi != yi- All prerequisite relationships are distinct, that is,
dependencies[i] != dependencies[j]. - The given graph is a directed acyclic graph.
Related Topics:
Graph
Many people mentioned the solution which uses topological sort and greedily picking the classes with the most outdegrees. It is wrong considering the following example.
1 2 level 2
\ |
3 4 level 1
\ |
\ |
5 level 0
All classes have the same outdegree but we should take classes 1 and 2 first. The answer should be 3.
Then the 2nd idea is that we take the classes with the maximum level first.
But there is also counter example of this solution...
6
[[1,4],[2,4],[3,4],[3,5],[3,6]]
2
1 2 3
\ | / | \
4 5 6
The classes 1, 2, 3 are all at level 1, but we should take 3 first.
Then shall we sort on both level and outdegrees?
It's still wrong. Counter example below:
9
[[1,4],[1,5],[2,5],[2,6],[3,6],[3,7],[8,4],[8,5],[9,6],[9,7]]
3
Classes 1, 2, 3, 8, 9 have the same outdegree and level but we should pick 1, 2, 8 or 2, 3,9 first.
Anyway, these greedy ideas are incorrect.
Just for reference, I put the greedy solution using depth below.
// OJ: https://leetcode.com/problems/parallel-courses-ii/
// Author: github.com/lzl124631x
// Time: O((V + E) * logV)
// Space: O(V + E)
// NOTE: this is a wrong answer.
class Solution {
int dfs(vector<vector<int>> &G, vector<int> &level, int u) {
if (level[u] != -1) return level[u];
int d = 0;
for (int v : G[u]) d = max(d, dfs(G, level, v) + 1);
return level[u] = d;
}
public:
int minNumberOfSemesters(int N, vector<vector<int>>& E, int K) {
vector<vector<int>> G(N);
vector<int> indegree(N), level(N, -1);
for (auto &e : E) {
G[e[0] - 1].push_back(e[1] - 1);
indegree[e[1] - 1]++;
}
for (int i = 0; i < N; ++i) dfs(G, level, i);
auto cmp = [](vector<int> &a, vector<int> &b) { return a[1] < b[1]; };
priority_queue<vector<int>, vector<vector<int>>, decltype(cmp)> pq(cmp);
for (int i = 0; i < N; ++i) {
if (indegree[i] == 0) pq.push({ i, level[i] });
}
int ans = 0;
while (pq.size()) {
vector<vector<int>> next;
int cnt = 0;
while (pq.size() && cnt < K) {
int u = pq.top()[0];
pq.pop();
++cnt;
for (int v : G[u]) {
if (--indegree[v] == 0) next.push_back({ v, level[v] });
}
}
++ans;
for (auto &n : next) pq.push(n);
}
return ans;
}
};If the j-th bit of pre[i] is 1, then there is an edge from j to i.
Let dp[i] be the minimum number of semesters needed to take all the courses specified in i. If the j-th bit of i is 1, then j-th class is considered.
Trivial case: dp[0] = 0. It takes no semester to finish 0 courses.
Initialization: dp[i] = N because it won't take more than N semesters to finish all courses.
dp[i | s] = min( dp[i] + 1 | `s` is a non-empty subset of `next` and there are no more than K bits in `s`)
where `next` is the set of next available courses if courses in `i` are taken.
// OJ: https://leetcode.com/problems/parallel-courses-ii/
// Author: github.com/lzl124631x
// Time: O(3^N)
// Space: O(2^N)
class Solution {
public:
int minNumberOfSemesters(int N, vector<vector<int>>& E, int K) {
vector<int> pre(N), dp(1 << N, N);
for (auto &e : E) pre[e[1] - 1] |= 1 << (e[0] - 1);
dp[0] = 0;
for (int i = 0; i < (1 << N); ++i) {
int next = 0;
for (int j = 0; j < N; ++j) {
if ((i & pre[j]) == pre[j]) next |= 1 << j; // If the current course set `i` covers all the prerequisite classes of `j`-th class, we can take `j`-th class.
}
next &= ~i; // remove the classes that are already covered by `i`.
for (int s = next; s; s = (s - 1) & next) { // enumerate all the non-empty subset of `next`.
if (__builtin_popcount(s) <= K) dp[i | s] = min(dp[i | s], dp[i] + 1);
}
}
return dp.back();
}
};