1376. Time Needed to Inform All Employees

1376. Time Needed to Inform All Employees (Medium)

A company has n employees with a unique ID for each employee from 0 to n - 1. The head of the company has is the one with headID.

Each employee has one direct manager given in the manager array where manager[i] is the direct manager of the i-th employee, manager[headID] = -1. Also it's guaranteed that the subordination relationships have a tree structure.

The head of the company wants to inform all the employees of the company of an urgent piece of news. He will inform his direct subordinates and they will inform their subordinates and so on until all employees know about the urgent news.

The i-th employee needs informTime[i] minutes to inform all of his direct subordinates (i.e After informTime[i] minutes, all his direct subordinates can start spreading the news).

Return the number of minutes needed to inform all the employees about the urgent news.

 

Example 1:

Input: n = 1, headID = 0, manager = [-1], informTime = [0]
Output: 0
Explanation: The head of the company is the only employee in the company.

Example 2:

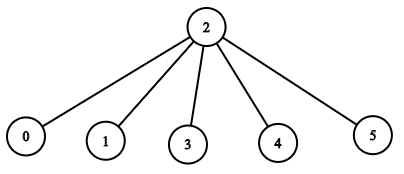
Input: n = 6, headID = 2, manager = [2,2,-1,2,2,2], informTime = [0,0,1,0,0,0]
Output: 1
Explanation: The head of the company with id = 2 is the direct manager of all the employees in the company and needs 1 minute to inform them all.
The tree structure of the employees in the company is shown.

Example 3:

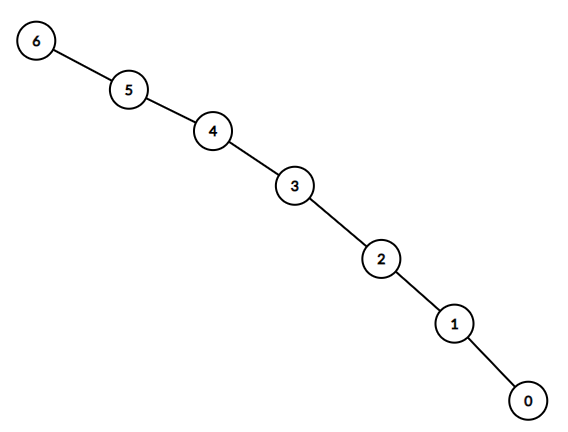
Input: n = 7, headID = 6, manager = [1,2,3,4,5,6,-1], informTime = [0,6,5,4,3,2,1]
Output: 21
Explanation: The head has id = 6. He will inform employee with id = 5 in 1 minute.
The employee with id = 5 will inform the employee with id = 4 in 2 minutes.
The employee with id = 4 will inform the employee with id = 3 in 3 minutes.
The employee with id = 3 will inform the employee with id = 2 in 4 minutes.
The employee with id = 2 will inform the employee with id = 1 in 5 minutes.
The employee with id = 1 will inform the employee with id = 0 in 6 minutes.
Needed time = 1 + 2 + 3 + 4 + 5 + 6 = 21.

Example 4:

Input: n = 15, headID = 0, manager = [-1,0,0,1,1,2,2,3,3,4,4,5,5,6,6], informTime = [1,1,1,1,1,1,1,0,0,0,0,0,0,0,0]
Output: 3
Explanation: The first minute the head will inform employees 1 and 2.
The second minute they will inform employees 3, 4, 5 and 6.
The third minute they will inform the rest of employees.

Example 5:

Input: n = 4, headID = 2, manager = [3,3,-1,2], informTime = [0,0,162,914]
Output: 1076

 

Constraints:

• 1 <= n <= 10^5
• 0 <= headID < n
• manager.length == n
• 0 <= manager[i] < n
• manager[headID] == -1
• informTime.length == n
• 0 <= informTime[i] <= 1000
• informTime[i] == 0 if employee i has no subordinates.
• It is guaranteed that all the employees can be informed.

Related Topics:
Depth-first Search

Similar Questions:

• Maximum Depth of Binary Tree (Easy)
• Binary Tree Maximum Path Sum (Hard)

Solution 1. BFS

Build the tree then get the maximum aggregated informTime (i.e. the sum of informTime starting from headID to the current node) of each (leaf) node.

// OJ: https://leetcode.com/problems/time-needed-to-inform-all-employees/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
class Solution {
public:
    int numOfMinutes(int n, int headID, vector<int>& manager, vector<int>& informTime) {
        unordered_map<int, vector<int>> m; // manager => subordinates
        for (int i = 0; i < n; ++i) m[manager[i]].push_back(i);
        queue<pair<int, int>> q;
        int ans = 0;
        q.emplace(headID, informTime[headID]);
        while (q.size()) {
            int cnt = q.size();
            while (cnt--) {
                auto p = q.front();
                q.pop();
                ans = max(ans, p.second);
                for (int sub : m[p.first]) q.push({ sub, p.second + informTime[sub] });
            }
        }
        return ans;
    }
};

Solution 2. DFS

Same idea as Solution 1 but using DFS.

BTW, using vector<vector<int>> can boost the speed a lot comparing with unordered_map<int, vector<int>>.

// OJ: https://leetcode.com/problems/time-needed-to-inform-all-employees/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
class Solution {
    vector<vector<int>> m; // manager => subordinates
    int dfs(int id, vector<int>& time) {
        int ans = 0;
        for (int n : m[id]) ans = max(ans, dfs(n, time));
        return time[id] + ans;
    } 
public:
    int numOfMinutes(int n, int headID, vector<int>& manager, vector<int>& informTime) {
        m.resize(n);
        for (int i = 0; i < n; ++i) {
            if (manager[i] == -1) continue;
            m[manager[i]].push_back(i);
        }
        return dfs(headID, informTime);
    }
};