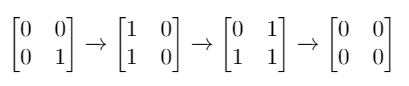1284. Minimum Number of Flips to Convert Binary Matrix to Zero Matrix

1284. Minimum Number of Flips to Convert Binary Matrix to Zero Matrix (Hard)

Given a m x n binary matrix mat. In one step, you can choose one cell and flip it and all the four neighbours of it if they exist (Flip is changing 1 to 0 and 0 to 1). A pair of cells are called neighboors if they share one edge.

Return the minimum number of steps required to convert mat to a zero matrix or -1 if you cannot.

Binary matrix is a matrix with all cells equal to 0 or 1 only.

Zero matrix is a matrix with all cells equal to 0.

 

Example 1:

Input: mat = [[0,0],[0,1]]
Output: 3
Explanation: One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.

Example 2:

Input: mat = [[0]]
Output: 0
Explanation: Given matrix is a zero matrix. We don't need to change it.

Example 3:

Input: mat = [[1,1,1],[1,0,1],[0,0,0]]
Output: 6

Example 4:

Input: mat = [[1,0,0],[1,0,0]]
Output: -1
Explanation: Given matrix can't be a zero matrix

 

Constraints:

• m == mat.length
• n == mat[0].length
• 1 <= m <= 3
• 1 <= n <= 3
• mat[i][j] is 0 or 1.

Related Topics:
Breadth-first Search

Solution 1. Bit vector + BFS

// OJ: https://leetcode.com/problems/minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix/
// Author: github.com/lzl124631x
// Time: O(MN * 2^(MN))
// Space: O(2^(MN))
class Solution {
public:
    int minFlips(vector<vector<int>>& A) {
        int start = 0, M = A.size(), N = A[0].size(), step = 0, dirs[5] = {1,0,-1,0,1};
        for (int i = 0; i < M; ++i) {
            for (int j = 0; j < N; ++j) {
                start |= (A[i][j] << (i * 3 + j));
            }
        }
        queue<int> q;
        unordered_set<int> s;
        q.push(start);
        s.insert(start);
        while (q.size()) {
            int cnt = q.size();
            while (cnt--) {
                int state = q.front();
                q.pop();
                if (state == 0) return step;
                for (int i = 0; i < 9; ++i) {
                    int next = state, r = i / 3, c = i % 3;
                    next ^= (1 << (r * 3 + c));
                    for (int j = 0; j < 4; ++j) {
                        int x = r + dirs[j], y = c + dirs[j + 1];
                        if (x < 0 || x >= M || y < 0 || y >= N) continue;
                        next ^= (1 << (x * 3 + y));
                    }
                    if (s.count(next) == 0) {
                        q.push(next);
                        s.insert(next);
                    }
                }
            }
            ++step;
        }
        return -1;
    }
};