diff --git a/CRAN-SUBMISSION b/CRAN-SUBMISSION
index 4576968..52b35db 100644
--- a/CRAN-SUBMISSION
+++ b/CRAN-SUBMISSION
@@ -1,3 +1,3 @@
-Version: 1.1.3
-Date: 2022-12-24 06:05:19 UTC
-SHA: 4bb05b0a4dd334ff96db8db1a4fbf5b8f61a3db7
+Version: 2.0.0
+Date: 2023-10-20 04:03:09 UTC
+SHA: 0db73d96940765d14af0154b85d419edc5b71b55
diff --git a/DESCRIPTION b/DESCRIPTION
index d6a6eec..1f94a92 100644
--- a/DESCRIPTION
+++ b/DESCRIPTION
@@ -1,12 +1,13 @@
Package: diffeqr
Type: Package
Title: Solving Differential Equations (ODEs, SDEs, DDEs, DAEs)
-Version: 1.1.3
+Version: 2.0.0
Authors@R: person("Christopher", "Rackauckas", email = "me@chrisrackauckas.com", role = c("aut", "cre", "cph"))
Description: An interface to 'DifferentialEquations.jl' from the R programming language.
It has unique high performance methods for solving ordinary differential equations (ODE), stochastic differential equations (SDE),
delay differential equations (DDE), differential-algebraic equations (DAE), and more. Much of the functionality,
including features like adaptive time stepping in SDEs, are unique and allow for multiple orders of magnitude speedup over more common methods.
+ Supports GPUs, with support for CUDA (NVIDIA), AMD GPUs, Intel oneAPI GPUs, and Apple's Metal (M-series chip GPUs).
'diffeqr' attaches an R interface onto the package, allowing seamless use of this tooling by R users. For more information,
see Rackauckas and Nie (2017) .
Depends: R (>= 3.4.0)
diff --git a/NEWS.md b/NEWS.md
index f951301..65cf01f 100644
--- a/NEWS.md
+++ b/NEWS.md
@@ -1,3 +1,8 @@
+## Release v2.0.0
+
+Support new DiffEqGPU syntax. This requires passing a backend. Supports NVIDIA CUDA, Intel OneAPI,
+AMD GPUs, and Apple Metal GPUs. Also much faster GPU compilation and runtime performance.
+
## Release v1.1.2
Bugfixes for newer Julia versions.
diff --git a/R/diffeqr.R b/R/diffeqr.R
index 7e4962f..7f613fd 100644
--- a/R/diffeqr.R
+++ b/R/diffeqr.R
@@ -117,20 +117,47 @@ jitoptimize_sde <- function (de,prob){
#' This function initializes the DiffEqGPU package for GPU-parallelized ensembles.
#' The first time will be long since it includes precompilation.
#'
+#' @param backend the backend for the GPU computation. Choices are "CUDA", "AMDGPU", "Metal", or "oneAPI"
+#'
#' @examples
#'
#' \dontrun{ ## diffeq_setup() is time-consuming and requires Julia+DifferentialEquations.jl
#'
-#' degpu <- diffeqr::diffeqgpu_setup()
+#' degpu <- diffeqr::diffeqgpu_setup(backend="CUDA")
#'
#' }
#'
#' @export
-diffeqgpu_setup <- function (){
+diffeqgpu_setup <- function (backend){
JuliaCall::julia_install_package_if_needed("DiffEqGPU")
JuliaCall::julia_library("DiffEqGPU")
functions <- JuliaCall::julia_eval("filter(isascii, replace.(string.(propertynames(DiffEqGPU)),\"!\"=>\"_bang\"))")
degpu <- julia_pkg_import("DiffEqGPU",functions)
+
+ if (backend == "CUDA") {
+ JuliaCall::julia_install_package_if_needed("CUDA")
+ JuliaCall::julia_library("CUDA")
+ backend <- julia_pkg_import("CUDA",c("CUDABackend"))
+ degpu$CUDABackend <- backend$CUDABackend
+ } else if (backend == "AMDGPU") {
+ JuliaCall::julia_install_package_if_needed("AMDGPU")
+ JuliaCall::julia_library("AMDGPU")
+ backend <- julia_pkg_import("AMDGPU",c("AMDGPUBackend"))
+ degpu$AMDGPUBackend <- backend$AMDGPUBackend
+ } else if (backend == "Metal") {
+ JuliaCall::julia_install_package_if_needed("Metal")
+ JuliaCall::julia_library("Metal")
+ backend <- julia_pkg_import("Metal",c("MetalBackend"))
+ degpu$MetalBackend <- backend$MetalBackend
+ } else if (backend == "oneAPI") {
+ JuliaCall::julia_install_package_if_needed("oneAPI")
+ JuliaCall::julia_library("oneAPI")
+ backend <- julia_pkg_import("oneAPI",c("oneAPIBackend"))
+ degpu$oneAPIBackend <- backend$oneAPIBackend
+ } else {
+ stop(paste("Illegal backend choice found. Allowed choices: CUDA, AMDGPU, Metal, and oneAPI. Chosen backend: ", backend))
+ }
+ degpu
}
julia_function <- function(func_name, pkg_name = "Main",
diff --git a/README.md b/README.md
index d6f1e4b..d784557 100644
--- a/README.md
+++ b/README.md
@@ -1,674 +1,700 @@
-# diffeqr
-
-[](https://gitter.im/JuliaDiffEq/Lobby?utm_source=badge&utm_medium=badge&utm_campaign=pr-badge&utm_content=badge)
-[](https://cran.r-project.org/package=diffeqr)
-[](https://github.com/SciML/diffeqr/actions)
-
-diffeqr is a package for solving differential equations in R. It utilizes
-[DifferentialEquations.jl](https://diffeq.sciml.ai/dev/) for its core routines
-to give high performance solving of ordinary differential equations (ODEs),
-stochastic differential equations (SDEs), delay differential equations (DDEs), and
-differential-algebraic equations (DAEs) directly in R.
-
-If you have any questions, or just want to chat about solvers/using the package,
-please feel free to chat in the [Gitter channel](https://gitter.im/JuliaDiffEq/Lobby?utm_source=badge&utm_medium=badge&utm_campaign=pr-badge&utm_content=badge). For bug reports, feature requests, etc., please submit an issue.
-
-## Installation
-
-[diffeqr is registered into CRAN](https://CRAN.R-project.org/package=diffeqr). Thus to add the package, use:
-
-```R
-install.packages("diffeqr")
-```
-
-To install the master branch of the package (for developers), use:
-
-```R
-devtools::install_github('SciML/diffeqr', build_vignettes=T)
-```
-
-Note that the first invocation of
-`diffeqr::diffeq_setup()` will install both Julia
-and the required packages if they are missing.
-If you wish to have it use an existing Julia binary,
-make sure that `julia` is found in the path. For more
-information see the `julia_setup()` function from
-[JuliaCall](https://github.com/Non-Contradiction/JuliaCall).
-
-## Usage
-
-diffeqr provides a direct wrapper over [DifferentialEquations.jl](https://diffeq.sciml.ai).
-The namespace is setup so that the standard syntax of Julia translates directly
-over to the R environment. There are two things to keep in mind:
-
-1. All DifferentialEquations.jl commands are prefaced by `de$`
-2. All commands with a `!` are replaced with `_bang`, for example `solve!` becomes `solve_bang`.
-
-## Ordinary Differential Equation (ODE) Examples
-
-### 1D Linear ODEs
-
-Let's solve the linear ODE `u'=1.01u`. First setup the package:
-
-```R
-de <- diffeqr::diffeq_setup()
-```
-
-Define the derivative function `f(u,p,t)`.
-
-```R
-f <- function(u,p,t) {
- return(1.01*u)
-}
-```
-
-Then we give it an initial condition and a time span to solve over:
-
-```R
-u0 <- 1/2
-tspan <- c(0., 1.)
-```
-
-With those pieces we define the `ODEProblem` and `solve` the ODE:
-
-```R
-prob = de$ODEProblem(f, u0, tspan)
-sol = de$solve(prob)
-```
-
-This gives back a solution object for which `sol$t` are the time points
-and `sol$u` are the values. We can treat the solution as a continuous object
-in time via
-
-```R
-sol$.(0.2)
-```
-
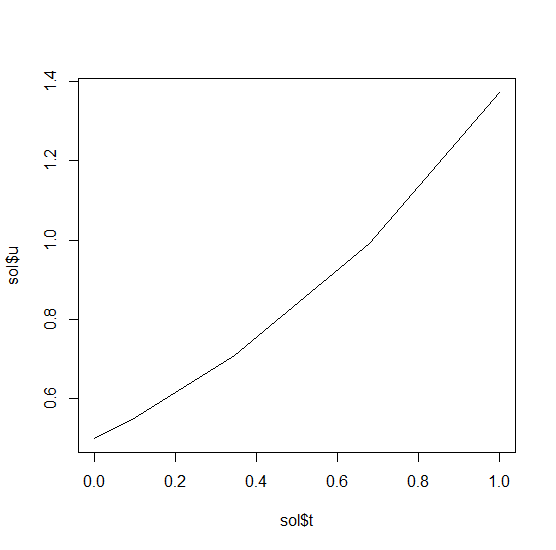
-and a high order interpolation will compute the value at `t=0.2`. We can check
-the solution by plotting it:
-
-```R
-plot(sol$t,sol$u,"l")
-```
-
-
-
-### Systems of ODEs
-
-Now let's solve the Lorenz equations. In this case, our initial condition is a vector and our derivative functions
-takes in the vector to return a vector (note: arbitrary dimensional arrays are allowed). We would define this as:
-
-```R
-f <- function(u,p,t) {
- du1 = p[1]*(u[2]-u[1])
- du2 = u[1]*(p[2]-u[3]) - u[2]
- du3 = u[1]*u[2] - p[3]*u[3]
- return(c(du1,du2,du3))
-}
-```
-
-Here we utilized the parameter array `p`. Thus we use `diffeqr::ode.solve` like before, but also pass in parameters this time:
-
-```R
-u0 <- c(1.0,0.0,0.0)
-tspan <- c(0.0,100.0)
-p <- c(10.0,28.0,8/3)
-prob <- de$ODEProblem(f, u0, tspan, p)
-sol <- de$solve(prob)
-```
-
-The returned solution is like before except now `sol$u` is an array of arrays,
-where `sol$u[i]` is the full system at time `sol$t[i]`. It can be convenient to
-turn this into an R matrix through `sapply`:
-
-```R
-mat <- sapply(sol$u,identity)
-```
-
-This has each row as a time series. `t(mat)` makes each column a time series.
-It is sometimes convenient to turn the output into a `data.frame` which is done
-via:
-
-```R
-udf <- as.data.frame(t(mat))
-```
-
-Now we can use `matplot` to plot the timeseries together:
-
-```R
-matplot(sol$t,udf,"l",col=1:3)
-```
-
-
-
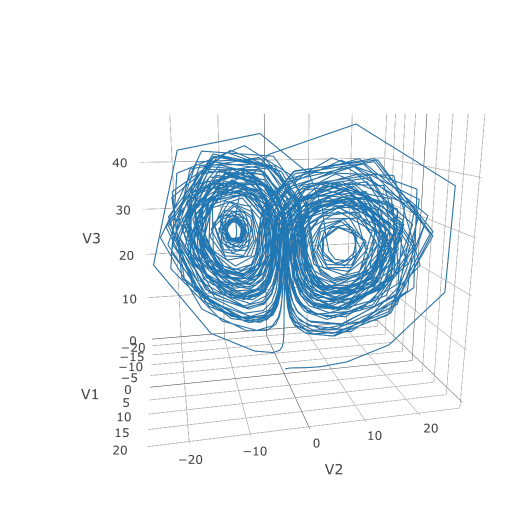
-Now we can use the Plotly package to draw a phase plot:
-
-```R
-plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')
-```
-
-
-
-Plotly is much prettier!
-
-### Option Handling
-
-If we want to have a more accurate solution, we can send `abstol` and `reltol`. Defaults are `1e-6` and `1e-3` respectively.
-Generally you can think of the digits of accuracy as related to 1 plus the exponent of the relative tolerance, so the default is
-two digits of accuracy. Absolute tolernace is the accuracy near 0.
-
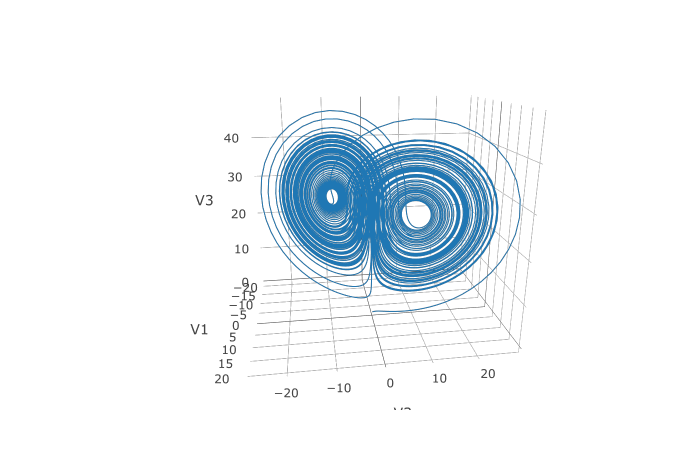
-In addition, we may want to choose to save at more time points. We do this by giving an array of values to save at as `saveat`.
-Together, this looks like:
-
-```R
-abstol <- 1e-8
-reltol <- 1e-8
-saveat <- 0:10000/100
-sol <- de$solve(prob,abstol=abstol,reltol=reltol,saveat=saveat)
-udf <- as.data.frame(t(sapply(sol$u,identity)))
-plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')
-```
-
-
-
-We can also choose to use a different algorithm. The choice is done using a string that matches the Julia syntax. See
-[the ODE tutorial for details](https://diffeq.sciml.ai/dev/tutorials/ode_example/#Choosing-a-Solver-Algorithm-1).
-The list of choices for ODEs can be found at the [ODE Solvers page](https://diffeq.sciml.ai/dev/solvers/ode_solve/).
-For example, let's use a 9th order method due to Verner:
-
-```R
-sol <- de$solve(prob,de$Vern9(),abstol=abstol,reltol=reltol,saveat=saveat)
-```
-
-Note that each algorithm choice will cause a JIT compilation.
-
-## Performance Enhancements
-
-One way to enhance the performance of your code is to define the function in Julia
-so that way it is JIT compiled. diffeqr is built using
-[the JuliaCall package](https://github.com/Non-Contradiction/JuliaCall), and so
-you can utilize the Julia JIT compiler. We expose this automatically over ODE
-functions via `jitoptimize_ode`, like in the following example:
-
-```R
-f <- function(u,p,t) {
- du1 = p[1]*(u[2]-u[1])
- du2 = u[1]*(p[2]-u[3]) - u[2]
- du3 = u[1]*u[2] - p[3]*u[3]
- return(c(du1,du2,du3))
-}
-u0 <- c(1.0,0.0,0.0)
-tspan <- c(0.0,100.0)
-p <- c(10.0,28.0,8/3)
-prob <- de$ODEProblem(f, u0, tspan, p)
-fastprob <- diffeqr::jitoptimize_ode(de,prob)
-sol <- de$solve(fastprob,de$Tsit5())
-```
-
-Note that the first evaluation of the function will have an ~2 second lag since
-the compiler will run, and all subsequent runs will be orders of magnitude faster
-than the pure R function. This means it's great for expensive functions (ex. large
-PDEs) or functions called repeatedly, like during optimization of parameters.
-
-We can also use the JuliaCall functions to directly define the function in Julia
-to eliminate the R interpreter overhead and get full JIT compilation:
-
-```R
-julf <- JuliaCall::julia_eval("
-function julf(du,u,p,t)
- du[1] = 10.0*(u[2]-u[1])
- du[2] = u[1]*(28.0-u[3]) - u[2]
- du[3] = u[1]*u[2] - (8/3)*u[3]
-end")
-JuliaCall::julia_assign("u0", u0)
-JuliaCall::julia_assign("p", p)
-JuliaCall::julia_assign("tspan", tspan)
-prob3 = JuliaCall::julia_eval("ODEProblem(julf, u0, tspan, p)")
-sol = de$solve(prob3,de$Tsit5())
-```
-
-To demonstrate the performance advantage, let's time them all:
-
-```R
-> system.time({ for (i in 1:100){ de$solve(prob ,de$Tsit5()) }})
- user system elapsed
- 6.69 0.06 6.78
-> system.time({ for (i in 1:100){ de$solve(fastprob,de$Tsit5()) }})
- user system elapsed
- 0.11 0.03 0.14
-> system.time({ for (i in 1:100){ de$solve(prob3 ,de$Tsit5()) }})
- user system elapsed
- 0.14 0.02 0.15
-```
-
-This is about a 50x improvement!
-
-#### Limitations of the JIT Compilation
-
-Using Julia's [ModelingToolkit](https://github.com/SciML/ModelingToolkit.jl)
-for tracing to JIT compile via Julia has a few known limitations:
-
-- It requires that all of the function calls are tracable. Scalar functions
- like `cos` and `sin` all fall into this category. Notably, matrix multiplication
- is not supported.
-- It will have a compilation lag on the first call.
-
-## Stochastic Differential Equation (SDE) Examples
-
-### 1D SDEs
-
-Solving stochastic differential equations (SDEs) is the similar to ODEs. To solve an SDE, you use `diffeqr::sde.solve` and give
-two functions: `f` and `g`, where `du = f(u,t)dt + g(u,t)dW_t`
-
-```r
-de <- diffeqr::diffeq_setup()
-f <- function(u,p,t) {
- return(1.01*u)
-}
-g <- function(u,p,t) {
- return(0.87*u)
-}
-u0 <- 1/2
-tspan <- c(0.0,1.0)
-prob <- de$SDEProblem(f,g,u0,tspan)
-sol <- de$solve(prob)
-udf <- as.data.frame(t(sapply(sol$u,identity)))
-plotly::plot_ly(udf, x = sol$t, y = sol$u, type = 'scatter', mode = 'lines')
-```
-
-
-
-### Systems of Diagonal Noise SDEs
-
-Let's add diagonal multiplicative noise to the Lorenz attractor. diffeqr defaults to diagonal noise when a system of
-equations is given. This is a unique noise term per system variable. Thus we generalize our previous functions as
-follows:
-
-```R
-f <- function(u,p,t) {
- du1 = p[1]*(u[2]-u[1])
- du2 = u[1]*(p[2]-u[3]) - u[2]
- du3 = u[1]*u[2] - p[3]*u[3]
- return(c(du1,du2,du3))
-}
-g <- function(u,p,t) {
- return(c(0.3*u[1],0.3*u[2],0.3*u[3]))
-}
-u0 <- c(1.0,0.0,0.0)
-tspan <- c(0.0,1.0)
-p <- c(10.0,28.0,8/3)
-prob <- de$SDEProblem(f,g,u0,tspan,p)
-sol <- de$solve(prob,saveat=0.005)
-udf <- as.data.frame(t(sapply(sol$u,identity)))
-plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')
-```
-
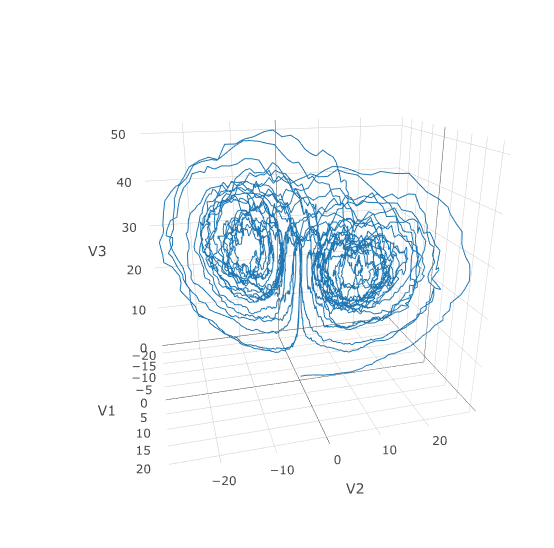
-Using a JIT compiled function for the drift and diffusion functions can greatly enhance the speed here.
-With the speed increase we can comfortably solve over long time spans:
-
-```R
-tspan <- c(0.0,100.0)
-prob <- de$SDEProblem(f,g,u0,tspan,p)
-fastprob <- diffeqr::jitoptimize_sde(de,prob)
-sol <- de$solve(fastprob,saveat=0.005)
-udf <- as.data.frame(t(sapply(sol$u,identity)))
-plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')
-```
-
-
-
-Let's see how much faster the JIT-compiled version was:
-
-```R
-> system.time({ for (i in 1:5){ de$solve(prob ) }})
- user system elapsed
- 146.40 0.75 147.22
-> system.time({ for (i in 1:5){ de$solve(fastprob) }})
- user system elapsed
- 1.07 0.10 1.17
-```
-
-Holy Monster's Inc. that's about 145x faster.
-
-### Systems of SDEs with Non-Diagonal Noise
-
-In many cases you may want to share noise terms across the system. This is known as non-diagonal noise. The
-[DifferentialEquations.jl SDE Tutorial](https://diffeq.sciml.ai/dev/tutorials/sde_example/#Example-4:-Systems-of-SDEs-with-Non-Diagonal-Noise-1)
-explains how the matrix form of the diffusion term corresponds to the summation style of multiple Wiener processes. Essentially,
-the row corresponds to which system the term is applied to, and the column is which noise term. So `du[i,j]` is the amount of
-noise due to the `j`th Wiener process that's applied to `u[i]`. We solve the Lorenz system with correlated noise as follows:
-
-```R
-f <- JuliaCall::julia_eval("
-function f(du,u,p,t)
- du[1] = 10.0*(u[2]-u[1])
- du[2] = u[1]*(28.0-u[3]) - u[2]
- du[3] = u[1]*u[2] - (8/3)*u[3]
-end")
-g <- JuliaCall::julia_eval("
-function g(du,u,p,t)
- du[1,1] = 0.3u[1]
- du[2,1] = 0.6u[1]
- du[3,1] = 0.2u[1]
- du[1,2] = 1.2u[2]
- du[2,2] = 0.2u[2]
- du[3,2] = 0.3u[2]
-end")
-u0 <- c(1.0,0.0,0.0)
-tspan <- c(0.0,100.0)
-noise_rate_prototype <- matrix(c(0.0,0.0,0.0,0.0,0.0,0.0), nrow = 3, ncol = 2)
-
-JuliaCall::julia_assign("u0", u0)
-JuliaCall::julia_assign("tspan", tspan)
-JuliaCall::julia_assign("noise_rate_prototype", noise_rate_prototype)
-prob <- JuliaCall::julia_eval("SDEProblem(f, g, u0, tspan, p, noise_rate_prototype=noise_rate_prototype)")
-sol <- de$solve(prob)
-udf <- as.data.frame(t(sapply(sol$u,identity)))
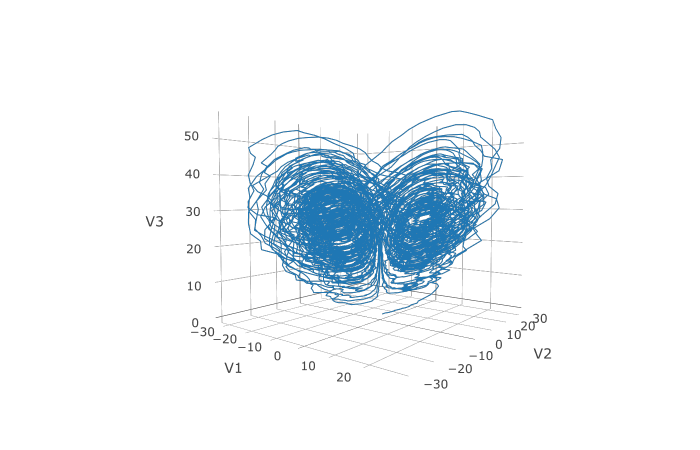
-plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')
-```
-
-
-
-Here you can see that the warping effect of the noise correlations is quite visible!
-Note that we applied JIT compilation since it's quite necessary for any difficult
-stochastic example.
-
-## Differential-Algebraic Equation (DAE) Examples
-
-A differential-algebraic equation is defined by an implicit function `f(du,u,p,t)=0`. All of the controls are the
-same as the other examples, except here you define a function which returns the residuals for each part of the equation
-to define the DAE. The initial value `u0` and the initial derivative `du0` are required, though they do not necessarily
-have to satisfy `f` (known as inconsistent initial conditions). The methods will automatically find consistent initial
-conditions. In order for this to occur, `differential_vars` must be set. This vector states which of the variables are
-differential (have a derivative term), with `false` meaning that the variable is purely algebraic.
-
-This example shows how to solve the Robertson equation:
-
-```R
-f <- function (du,u,p,t) {
- resid1 = - 0.04*u[1] + 1e4*u[2]*u[3] - du[1]
- resid2 = + 0.04*u[1] - 3e7*u[2]^2 - 1e4*u[2]*u[3] - du[2]
- resid3 = u[1] + u[2] + u[3] - 1.0
- c(resid1,resid2,resid3)
-}
-u0 <- c(1.0, 0, 0)
-du0 <- c(-0.04, 0.04, 0.0)
-tspan <- c(0.0,100000.0)
-differential_vars <- c(TRUE,TRUE,FALSE)
-prob <- de$DAEProblem(f,du0,u0,tspan,differential_vars=differential_vars)
-sol <- de$solve(prob)
-udf <- as.data.frame(t(sapply(sol$u,identity)))
-plotly::plot_ly(udf, x = sol$t, y = ~V1, type = 'scatter', mode = 'lines') |>
- plotly::add_trace(y = ~V2) |>
- plotly::add_trace(y = ~V3)
-```
-
-Additionally, an in-place JIT compiled form for `f` can be used to enhance the speed:
-
-```R
-f = JuliaCall::julia_eval("function f(out,du,u,p,t)
- out[1] = - 0.04u[1] + 1e4*u[2]*u[3] - du[1]
- out[2] = + 0.04u[1] - 3e7*u[2]^2 - 1e4*u[2]*u[3] - du[2]
- out[3] = u[1] + u[2] + u[3] - 1.0
-end")
-u0 <- c(1.0, 0, 0)
-du0 <- c(-0.04, 0.04, 0.0)
-tspan <- c(0.0,100000.0)
-differential_vars <- c(TRUE,TRUE,FALSE)
-JuliaCall::julia_assign("du0", du0)
-JuliaCall::julia_assign("u0", u0)
-JuliaCall::julia_assign("p", p)
-JuliaCall::julia_assign("tspan", tspan)
-JuliaCall::julia_assign("differential_vars", differential_vars)
-prob = JuliaCall::julia_eval("DAEProblem(f, du0, u0, tspan, p, differential_vars=differential_vars)")
-sol = de$solve(prob)
-```
-
-
-
-## Delay Differential Equation (DDE) Examples
-
-A delay differential equation is an ODE which allows the use of previous values. In this case, the function
-needs to be a JIT compiled Julia function. It looks just like the ODE, except in this case there is a function
-`h(p,t)` which allows you to interpolate and grab previous values.
-
-We must provide a history function `h(p,t)` that gives values for `u` before
-`t0`. Here we assume that the solution was constant before the initial time point. Additionally, we pass
-`constant_lags = c(20.0)` to tell the solver that only constant-time lags were used and what the lag length
-was. This helps improve the solver accuracy by accurately stepping at the points of discontinuity. Together
-this is:
-
-```R
-f <- JuliaCall::julia_eval("function f(du, u, h, p, t)
- du[1] = 1.1/(1 + sqrt(10)*(h(p, t-20)[1])^(5/4)) - 10*u[1]/(1 + 40*u[2])
- du[2] = 100*u[1]/(1 + 40*u[2]) - 2.43*u[2]
-end")
-h <- JuliaCall::julia_eval("function h(p, t)
- [1.05767027/3, 1.030713491/3]
-end")
-u0 <- c(1.05767027/3, 1.030713491/3)
-tspan <- c(0.0, 100.0)
-constant_lags <- c(20.0)
-JuliaCall::julia_assign("u0", u0)
-JuliaCall::julia_assign("tspan", tspan)
-JuliaCall::julia_assign("constant_lags", tspan)
-prob <- JuliaCall::julia_eval("DDEProblem(f, u0, h, tspan, constant_lags = constant_lags)")
-sol <- de$solve(prob,de$MethodOfSteps(de$Tsit5()))
-udf <- as.data.frame(t(sapply(sol$u,identity)))
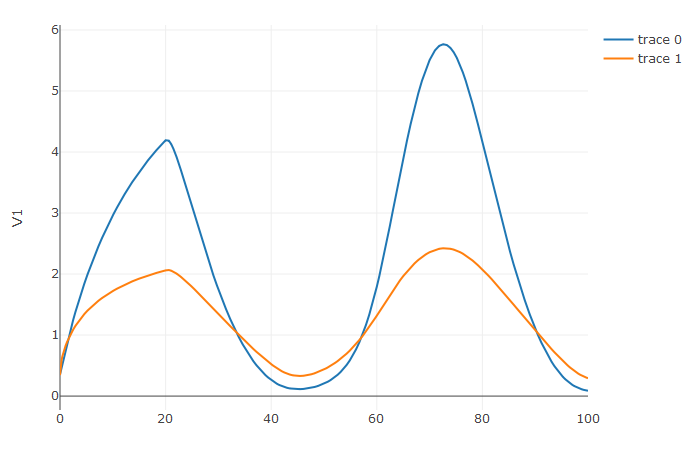
-plotly::plot_ly(udf, x = sol$t, y = ~V1, type = 'scatter', mode = 'lines') |> plotly::add_trace(y = ~V2)
-```
-
-
-
-Notice that the solver accurately is able to simulate the kink (discontinuity) at `t=20` due to the discontinuity
-of the derivative at the initial time point! This is why declaring discontinuities can enhance the solver accuracy.
-
-## GPU-Accelerated ODE Solving of Ensembles
-
-In many cases one is interested in solving the same ODE many times over many
-different initial conditions and parameters. In diffeqr parlance this is called
-an ensemble solve. diffeqr inherits the parallelism tools of the
-[SciML ecosystem](https://sciml.ai/) that are used for things like
-[automated equation discovery and acceleration](https://arxiv.org/abs/2001.04385).
-Here we will demonstrate using these parallel tools to accelerate the solving
-of an ensemble.
-
-First, let's define the JIT-accelerated Lorenz equation like before:
-
-```R
-de <- diffeqr::diffeq_setup()
-lorenz <- function (u,p,t){
- du1 = p[1]*(u[2]-u[1])
- du2 = u[1]*(p[2]-u[3]) - u[2]
- du3 = u[1]*u[2] - p[3]*u[3]
- c(du1,du2,du3)
-}
-u0 <- c(1.0,1.0,1.0)
-tspan <- c(0.0,100.0)
-p <- c(10.0,28.0,8/3)
-prob <- de$ODEProblem(lorenz,u0,tspan,p)
-fastprob <- diffeqr::jitoptimize_ode(de,prob)
-```
-
-Now we use the `EnsembleProblem` as defined on the
-[ensemble parallelism page of the documentation](https://diffeq.sciml.ai/stable/features/ensemble/):
-Let's build an ensemble by utilizing uniform random numbers to randomize the
-initial conditions and parameters:
-
-```R
-prob_func <- function (prob,i,rep){
- de$remake(prob,u0=runif(3)*u0,p=runif(3)*p)
-}
-ensembleprob = de$EnsembleProblem(fastprob, prob_func = prob_func, safetycopy=FALSE)
-```
-
-Now we solve the ensemble in serial:
-
-```R
-sol = de$solve(ensembleprob,de$Tsit5(),de$EnsembleSerial(),trajectories=10000,saveat=0.01)
-```
-
-To add GPUs to the mix, we need to bring in [DiffEqGPU](https://github.com/SciML/DiffEqGPU.jl).
-The `diffeqr::diffeqgpu_setup()` helper function will install CUDA for you and
-bring all of the bindings into the returned object:
-
-```R
-degpu <- diffeqr::diffeqgpu_setup()
-```
-
-Now we simply use `EnsembleGPUArray()` to solve 10,000 ODEs on the GPU in parallel:
-
-```R
-sol <- de$solve(ensembleprob,de$Tsit5(),degpu$EnsembleGPUArray(),trajectories=10000,saveat=0.01)
-```
-
-### Benchmark
-
-To see how much of an effect the parallelism has, let's test this against R's
-deSolve package. This is exactly the same problem as the documentation example
-for deSolve, so let's copy that verbatim and then add a function to do the
-ensemble generation:
-
-```R
-library(deSolve)
-Lorenz <- function(t, state, parameters) {
- with(as.list(c(state, parameters)), {
- dX <- a * X + Y * Z
- dY <- b * (Y - Z)
- dZ <- -X * Y + c * Y - Z
- list(c(dX, dY, dZ))
- })
-}
-
-parameters <- c(a = -8/3, b = -10, c = 28)
-state <- c(X = 1, Y = 1, Z = 1)
-times <- seq(0, 100, by = 0.01)
-out <- ode(y = state, times = times, func = Lorenz, parms = parameters)
-
-lorenz_solve <- function (i){
- state <- c(X = runif(1), Y = runif(1), Z = runif(1))
- parameters <- c(a = -8/3 * runif(1), b = -10 * runif(1), c = 28 * runif(1))
- out <- ode(y = state, times = times, func = Lorenz, parms = parameters)
-}
-```
-
-Using `lapply` to generate the ensemble we get:
-
-```
-> system.time({ lapply(1:1000,lorenz_solve) })
- user system elapsed
- 225.81 0.46 226.63
-```
-
-Now let's see how the JIT-accelerated serial Julia version stacks up against that:
-
-```
-> system.time({ de$solve(ensembleprob,de$Tsit5(),de$EnsembleSerial(),trajectories=1000,saveat=0.01) })
- user system elapsed
- 2.75 0.30 3.08
-```
-
-Julia is already about 73x faster than the pure R solvers here! Now let's add
-GPU-acceleration to the mix:
-
-```
-> system.time({ de$solve(ensembleprob,de$Tsit5(),degpu$EnsembleGPUArray(),trajectories=1000,saveat=0.01) })
- user system elapsed
- 1.33 1.57 2.93
-```
-
-That's only around 2x faster. But the GPU acceleartion is made for massively
-parallel problems, so let's up the trajectories a bit. We will not use more
-trajectories from R because that would take too much computing power, so let's
-see what happens to the Julia serial and GPU at 10,000 trajectories:
-
-```
-> system.time({ de$solve(ensembleprob,de$Tsit5(),de$EnsembleSerial(),trajectories=10000,saveat=0.01) })
- user system elapsed
- 35.02 4.19 39.25
-```
-
-```
-> system.time({ de$solve(ensembleprob,de$Tsit5(),degpu$EnsembleGPUArray(),trajectories=10000,saveat=0.01) })
- user system elapsed
- 12.03 3.57 15.60
-```
-
-To compare this to the pure Julia code:
-
-```julia
-using OrdinaryDiffEq, DiffEqGPU
-function lorenz(du,u,p,t)
- @inbounds begin
- du[1] = p[1]*(u[2]-u[1])
- du[2] = u[1]*(p[2]-u[3]) - u[2]
- du[3] = u[1]*u[2] - p[3]*u[3]
- end
- nothing
-end
-
-u0 = Float32[1.0;1.0;1.0]
-tspan = (0.0f0,100.0f0)
-p = [10.0f0,28.0f0,8/3f0]
-prob = ODEProblem(lorenz,u0,tspan,p)
-prob_func = (prob,i,repeat) -> remake(prob,u0=rand(Float32,3).*u0,p=rand(Float32,3).*p)
-monteprob = EnsembleProblem(prob, prob_func = prob_func, safetycopy=false)
-@time sol = solve(monteprob,Tsit5(),EnsembleGPUArray(),trajectories=10_000,saveat=0.01f0)
-
-# 9.444439 seconds (22.96 M allocations: 6.464 GiB, 44.53% gc time)
-```
-
-which is more than an order of magnitude faster for computing 10,000 trajectories,
-note that the major factors are that we cannot define 32-bit floating point values
-from R and the `prob_func` for generating the initial conditions and parameters
-is a major bottleneck since this function is written in R.
-
-To see how this scales in Julia, let's take it to insane heights. First, let's
-reduce the amount we're saving:
-
-```julia
-@time sol = solve(monteprob,Tsit5(),EnsembleGPUArray(),trajectories=10_000,saveat=1.0f0)
-# 0.801215 seconds (1.66 M allocations: 133.846 MiB)
-```
-
-This highlights that controlling memory pressure is key with GPU usage: you will
-get much better performance when requiring less saved points on the GPU.
-
-```julia
-@time sol = solve(monteprob,Tsit5(),EnsembleGPUArray(),trajectories=100_000,saveat=1.0f0)
-# 1.871536 seconds (6.66 M allocations: 919.521 MiB, 2.48% gc time)
-```
-
-compared to serial:
-
-```julia
-@time sol = solve(monteprob,Tsit5(),EnsembleSerial(),trajectories=100_000,saveat=1.0f0)
-# 22.136743 seconds (16.40 M allocations: 1.628 GiB, 42.98% gc time)
-```
-
-And now we start to see that scaling power! Let's solve 1 million trajectories:
-
-```julia
-@time sol = solve(monteprob,Tsit5(),EnsembleGPUArray(),trajectories=1_000_000,saveat=1.0f0)
-# 25.234710 seconds (56.53 M allocations: 8.579 GiB, 51.61% gc time)
-```
-
-For reference, let's look at deSolve with the change to only save that much:
-
-```R
-times <- seq(0, 100, by = 1.0)
-lorenz_solve <- function (i){
- state <- c(X = runif(1), Y = runif(1), Z = runif(1))
- parameters <- c(a = -8/3 * runif(1), b = -10 * runif(1), c = 28 * runif(1))
- out <- ode(y = state, times = times, func = Lorenz, parms = parameters)
-}
-
-system.time({ lapply(1:1000,lorenz_solve) })
-```
-
-The GPU version is solving 1000x as many trajectories, 2x as fast! So conclusion,
-if you need the most speed, you may want to move to the Julia version to get the
-most out of your GPU due to Float32's, and when using GPUs make sure it's a problem
-with a relatively average or low memory pressure, and these methods will give
-orders of magnitude acceleration compared to what you might be used to.
+# diffeqr
+
+[](https://gitter.im/JuliaDiffEq/Lobby?utm_source=badge&utm_medium=badge&utm_campaign=pr-badge&utm_content=badge)
+[](https://cran.r-project.org/package=diffeqr)
+[](https://github.com/SciML/diffeqr/actions)
+
+diffeqr is a package for solving differential equations in R. It utilizes
+[DifferentialEquations.jl](https://diffeq.sciml.ai/dev/) for its core routines
+to give high performance solving of ordinary differential equations (ODEs),
+stochastic differential equations (SDEs), delay differential equations (DDEs), and
+differential-algebraic equations (DAEs) directly in R.
+
+If you have any questions, or just want to chat about solvers/using the package,
+please feel free to chat in the [Gitter channel](https://gitter.im/JuliaDiffEq/Lobby?utm_source=badge&utm_medium=badge&utm_campaign=pr-badge&utm_content=badge). For bug reports, feature requests, etc., please submit an issue.
+
+## Installation
+
+[diffeqr is registered into CRAN](https://CRAN.R-project.org/package=diffeqr). Thus to add the package, use:
+
+```R
+install.packages("diffeqr")
+```
+
+To install the master branch of the package (for developers), use:
+
+```R
+devtools::install_github('SciML/diffeqr', build_vignettes=T)
+```
+
+Note that the first invocation of
+`diffeqr::diffeq_setup()` will install both Julia
+and the required packages if they are missing.
+If you wish to have it use an existing Julia binary,
+make sure that `julia` is found in the path. For more
+information see the `julia_setup()` function from
+[JuliaCall](https://github.com/Non-Contradiction/JuliaCall).
+
+## Usage
+
+diffeqr provides a direct wrapper over [DifferentialEquations.jl](https://diffeq.sciml.ai).
+The namespace is setup so that the standard syntax of Julia translates directly
+over to the R environment. There are two things to keep in mind:
+
+1. All DifferentialEquations.jl commands are prefaced by `de$`
+2. All commands with a `!` are replaced with `_bang`, for example `solve!` becomes `solve_bang`.
+
+## Ordinary Differential Equation (ODE) Examples
+
+### 1D Linear ODEs
+
+Let's solve the linear ODE `u'=1.01u`. First setup the package:
+
+```R
+de <- diffeqr::diffeq_setup()
+```
+
+Define the derivative function `f(u,p,t)`.
+
+```R
+f <- function(u,p,t) {
+ return(1.01*u)
+}
+```
+
+Then we give it an initial condition and a time span to solve over:
+
+```R
+u0 <- 1/2
+tspan <- c(0., 1.)
+```
+
+With those pieces we define the `ODEProblem` and `solve` the ODE:
+
+```R
+prob = de$ODEProblem(f, u0, tspan)
+sol = de$solve(prob)
+```
+
+This gives back a solution object for which `sol$t` are the time points
+and `sol$u` are the values. We can treat the solution as a continuous object
+in time via
+
+```R
+sol$.(0.2)
+```
+
+and a high order interpolation will compute the value at `t=0.2`. We can check
+the solution by plotting it:
+
+```R
+plot(sol$t,sol$u,"l")
+```
+
+
+
+### Systems of ODEs
+
+Now let's solve the Lorenz equations. In this case, our initial condition is a vector and our derivative functions
+takes in the vector to return a vector (note: arbitrary dimensional arrays are allowed). We would define this as:
+
+```R
+f <- function(u,p,t) {
+ du1 = p[1]*(u[2]-u[1])
+ du2 = u[1]*(p[2]-u[3]) - u[2]
+ du3 = u[1]*u[2] - p[3]*u[3]
+ return(c(du1,du2,du3))
+}
+```
+
+Here we utilized the parameter array `p`. Thus we use `diffeqr::ode.solve` like before, but also pass in parameters this time:
+
+```R
+u0 <- c(1.0,0.0,0.0)
+tspan <- c(0.0,100.0)
+p <- c(10.0,28.0,8/3)
+prob <- de$ODEProblem(f, u0, tspan, p)
+sol <- de$solve(prob)
+```
+
+The returned solution is like before except now `sol$u` is an array of arrays,
+where `sol$u[i]` is the full system at time `sol$t[i]`. It can be convenient to
+turn this into an R matrix through `sapply`:
+
+```R
+mat <- sapply(sol$u,identity)
+```
+
+This has each row as a time series. `t(mat)` makes each column a time series.
+It is sometimes convenient to turn the output into a `data.frame` which is done
+via:
+
+```R
+udf <- as.data.frame(t(mat))
+```
+
+Now we can use `matplot` to plot the timeseries together:
+
+```R
+matplot(sol$t,udf,"l",col=1:3)
+```
+
+
+
+Now we can use the Plotly package to draw a phase plot:
+
+```R
+plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')
+```
+
+
+
+Plotly is much prettier!
+
+### Option Handling
+
+If we want to have a more accurate solution, we can send `abstol` and `reltol`. Defaults are `1e-6` and `1e-3` respectively.
+Generally you can think of the digits of accuracy as related to 1 plus the exponent of the relative tolerance, so the default is
+two digits of accuracy. Absolute tolernace is the accuracy near 0.
+
+In addition, we may want to choose to save at more time points. We do this by giving an array of values to save at as `saveat`.
+Together, this looks like:
+
+```R
+abstol <- 1e-8
+reltol <- 1e-8
+saveat <- 0:10000/100
+sol <- de$solve(prob,abstol=abstol,reltol=reltol,saveat=saveat)
+udf <- as.data.frame(t(sapply(sol$u,identity)))
+plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')
+```
+
+
+
+We can also choose to use a different algorithm. The choice is done using a string that matches the Julia syntax. See
+[the ODE tutorial for details](https://diffeq.sciml.ai/dev/tutorials/ode_example/#Choosing-a-Solver-Algorithm-1).
+The list of choices for ODEs can be found at the [ODE Solvers page](https://diffeq.sciml.ai/dev/solvers/ode_solve/).
+For example, let's use a 9th order method due to Verner:
+
+```R
+sol <- de$solve(prob,de$Vern9(),abstol=abstol,reltol=reltol,saveat=saveat)
+```
+
+Note that each algorithm choice will cause a JIT compilation.
+
+## Performance Enhancements
+
+One way to enhance the performance of your code is to define the function in Julia
+so that way it is JIT compiled. diffeqr is built using
+[the JuliaCall package](https://github.com/Non-Contradiction/JuliaCall), and so
+you can utilize the Julia JIT compiler. We expose this automatically over ODE
+functions via `jitoptimize_ode`, like in the following example:
+
+```R
+f <- function(u,p,t) {
+ du1 = p[1]*(u[2]-u[1])
+ du2 = u[1]*(p[2]-u[3]) - u[2]
+ du3 = u[1]*u[2] - p[3]*u[3]
+ return(c(du1,du2,du3))
+}
+u0 <- c(1.0,0.0,0.0)
+tspan <- c(0.0,100.0)
+p <- c(10.0,28.0,8/3)
+prob <- de$ODEProblem(f, u0, tspan, p)
+fastprob <- diffeqr::jitoptimize_ode(de,prob)
+sol <- de$solve(fastprob,de$Tsit5())
+```
+
+Note that the first evaluation of the function will have an ~2 second lag since
+the compiler will run, and all subsequent runs will be orders of magnitude faster
+than the pure R function. This means it's great for expensive functions (ex. large
+PDEs) or functions called repeatedly, like during optimization of parameters.
+
+We can also use the JuliaCall functions to directly define the function in Julia
+to eliminate the R interpreter overhead and get full JIT compilation:
+
+```R
+julf <- JuliaCall::julia_eval("
+function julf(du,u,p,t)
+ du[1] = 10.0*(u[2]-u[1])
+ du[2] = u[1]*(28.0-u[3]) - u[2]
+ du[3] = u[1]*u[2] - (8/3)*u[3]
+end")
+JuliaCall::julia_assign("u0", u0)
+JuliaCall::julia_assign("p", p)
+JuliaCall::julia_assign("tspan", tspan)
+prob3 = JuliaCall::julia_eval("ODEProblem(julf, u0, tspan, p)")
+sol = de$solve(prob3,de$Tsit5())
+```
+
+To demonstrate the performance advantage, let's time them all:
+
+```R
+> system.time({ for (i in 1:100){ de$solve(prob ,de$Tsit5()) }})
+ user system elapsed
+ 6.69 0.06 6.78
+> system.time({ for (i in 1:100){ de$solve(fastprob,de$Tsit5()) }})
+ user system elapsed
+ 0.11 0.03 0.14
+> system.time({ for (i in 1:100){ de$solve(prob3 ,de$Tsit5()) }})
+ user system elapsed
+ 0.14 0.02 0.15
+```
+
+This is about a 50x improvement!
+
+#### Limitations of the JIT Compilation
+
+Using Julia's [ModelingToolkit](https://github.com/SciML/ModelingToolkit.jl)
+for tracing to JIT compile via Julia has a few known limitations:
+
+- It requires that all of the function calls are tracable. Scalar functions
+ like `cos` and `sin` all fall into this category. Notably, matrix multiplication
+ is not supported.
+- It will have a compilation lag on the first call.
+
+## Stochastic Differential Equation (SDE) Examples
+
+### 1D SDEs
+
+Solving stochastic differential equations (SDEs) is the similar to ODEs. To solve an SDE, you use `diffeqr::sde.solve` and give
+two functions: `f` and `g`, where `du = f(u,t)dt + g(u,t)dW_t`
+
+```r
+de <- diffeqr::diffeq_setup()
+f <- function(u,p,t) {
+ return(1.01*u)
+}
+g <- function(u,p,t) {
+ return(0.87*u)
+}
+u0 <- 1/2
+tspan <- c(0.0,1.0)
+prob <- de$SDEProblem(f,g,u0,tspan)
+sol <- de$solve(prob)
+udf <- as.data.frame(t(sapply(sol$u,identity)))
+plotly::plot_ly(udf, x = sol$t, y = sol$u, type = 'scatter', mode = 'lines')
+```
+
+
+
+### Systems of Diagonal Noise SDEs
+
+Let's add diagonal multiplicative noise to the Lorenz attractor. diffeqr defaults to diagonal noise when a system of
+equations is given. This is a unique noise term per system variable. Thus we generalize our previous functions as
+follows:
+
+```R
+f <- function(u,p,t) {
+ du1 = p[1]*(u[2]-u[1])
+ du2 = u[1]*(p[2]-u[3]) - u[2]
+ du3 = u[1]*u[2] - p[3]*u[3]
+ return(c(du1,du2,du3))
+}
+g <- function(u,p,t) {
+ return(c(0.3*u[1],0.3*u[2],0.3*u[3]))
+}
+u0 <- c(1.0,0.0,0.0)
+tspan <- c(0.0,1.0)
+p <- c(10.0,28.0,8/3)
+prob <- de$SDEProblem(f,g,u0,tspan,p)
+sol <- de$solve(prob,saveat=0.005)
+udf <- as.data.frame(t(sapply(sol$u,identity)))
+plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')
+```
+
+Using a JIT compiled function for the drift and diffusion functions can greatly enhance the speed here.
+With the speed increase we can comfortably solve over long time spans:
+
+```R
+tspan <- c(0.0,100.0)
+prob <- de$SDEProblem(f,g,u0,tspan,p)
+fastprob <- diffeqr::jitoptimize_sde(de,prob)
+sol <- de$solve(fastprob,saveat=0.005)
+udf <- as.data.frame(t(sapply(sol$u,identity)))
+plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')
+```
+
+
+
+Let's see how much faster the JIT-compiled version was:
+
+```R
+> system.time({ for (i in 1:5){ de$solve(prob ) }})
+ user system elapsed
+ 146.40 0.75 147.22
+> system.time({ for (i in 1:5){ de$solve(fastprob) }})
+ user system elapsed
+ 1.07 0.10 1.17
+```
+
+Holy Monster's Inc. that's about 145x faster.
+
+### Systems of SDEs with Non-Diagonal Noise
+
+In many cases you may want to share noise terms across the system. This is known as non-diagonal noise. The
+[DifferentialEquations.jl SDE Tutorial](https://diffeq.sciml.ai/dev/tutorials/sde_example/#Example-4:-Systems-of-SDEs-with-Non-Diagonal-Noise-1)
+explains how the matrix form of the diffusion term corresponds to the summation style of multiple Wiener processes. Essentially,
+the row corresponds to which system the term is applied to, and the column is which noise term. So `du[i,j]` is the amount of
+noise due to the `j`th Wiener process that's applied to `u[i]`. We solve the Lorenz system with correlated noise as follows:
+
+```R
+f <- JuliaCall::julia_eval("
+function f(du,u,p,t)
+ du[1] = 10.0*(u[2]-u[1])
+ du[2] = u[1]*(28.0-u[3]) - u[2]
+ du[3] = u[1]*u[2] - (8/3)*u[3]
+end")
+g <- JuliaCall::julia_eval("
+function g(du,u,p,t)
+ du[1,1] = 0.3u[1]
+ du[2,1] = 0.6u[1]
+ du[3,1] = 0.2u[1]
+ du[1,2] = 1.2u[2]
+ du[2,2] = 0.2u[2]
+ du[3,2] = 0.3u[2]
+end")
+u0 <- c(1.0,0.0,0.0)
+tspan <- c(0.0,100.0)
+noise_rate_prototype <- matrix(c(0.0,0.0,0.0,0.0,0.0,0.0), nrow = 3, ncol = 2)
+
+JuliaCall::julia_assign("u0", u0)
+JuliaCall::julia_assign("tspan", tspan)
+JuliaCall::julia_assign("noise_rate_prototype", noise_rate_prototype)
+prob <- JuliaCall::julia_eval("SDEProblem(f, g, u0, tspan, p, noise_rate_prototype=noise_rate_prototype)")
+sol <- de$solve(prob)
+udf <- as.data.frame(t(sapply(sol$u,identity)))
+plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')
+```
+
+
+
+Here you can see that the warping effect of the noise correlations is quite visible!
+Note that we applied JIT compilation since it's quite necessary for any difficult
+stochastic example.
+
+## Differential-Algebraic Equation (DAE) Examples
+
+A differential-algebraic equation is defined by an implicit function `f(du,u,p,t)=0`. All of the controls are the
+same as the other examples, except here you define a function which returns the residuals for each part of the equation
+to define the DAE. The initial value `u0` and the initial derivative `du0` are required, though they do not necessarily
+have to satisfy `f` (known as inconsistent initial conditions). The methods will automatically find consistent initial
+conditions. In order for this to occur, `differential_vars` must be set. This vector states which of the variables are
+differential (have a derivative term), with `false` meaning that the variable is purely algebraic.
+
+This example shows how to solve the Robertson equation:
+
+```R
+f <- function (du,u,p,t) {
+ resid1 = - 0.04*u[1] + 1e4*u[2]*u[3] - du[1]
+ resid2 = + 0.04*u[1] - 3e7*u[2]^2 - 1e4*u[2]*u[3] - du[2]
+ resid3 = u[1] + u[2] + u[3] - 1.0
+ c(resid1,resid2,resid3)
+}
+u0 <- c(1.0, 0, 0)
+du0 <- c(-0.04, 0.04, 0.0)
+tspan <- c(0.0,100000.0)
+differential_vars <- c(TRUE,TRUE,FALSE)
+prob <- de$DAEProblem(f,du0,u0,tspan,differential_vars=differential_vars)
+sol <- de$solve(prob)
+udf <- as.data.frame(t(sapply(sol$u,identity)))
+plotly::plot_ly(udf, x = sol$t, y = ~V1, type = 'scatter', mode = 'lines') |>
+ plotly::add_trace(y = ~V2) |>
+ plotly::add_trace(y = ~V3)
+```
+
+Additionally, an in-place JIT compiled form for `f` can be used to enhance the speed:
+
+```R
+f = JuliaCall::julia_eval("function f(out,du,u,p,t)
+ out[1] = - 0.04u[1] + 1e4*u[2]*u[3] - du[1]
+ out[2] = + 0.04u[1] - 3e7*u[2]^2 - 1e4*u[2]*u[3] - du[2]
+ out[3] = u[1] + u[2] + u[3] - 1.0
+end")
+u0 <- c(1.0, 0, 0)
+du0 <- c(-0.04, 0.04, 0.0)
+tspan <- c(0.0,100000.0)
+differential_vars <- c(TRUE,TRUE,FALSE)
+JuliaCall::julia_assign("du0", du0)
+JuliaCall::julia_assign("u0", u0)
+JuliaCall::julia_assign("p", p)
+JuliaCall::julia_assign("tspan", tspan)
+JuliaCall::julia_assign("differential_vars", differential_vars)
+prob = JuliaCall::julia_eval("DAEProblem(f, du0, u0, tspan, p, differential_vars=differential_vars)")
+sol = de$solve(prob)
+```
+
+
+
+## Delay Differential Equation (DDE) Examples
+
+A delay differential equation is an ODE which allows the use of previous values. In this case, the function
+needs to be a JIT compiled Julia function. It looks just like the ODE, except in this case there is a function
+`h(p,t)` which allows you to interpolate and grab previous values.
+
+We must provide a history function `h(p,t)` that gives values for `u` before
+`t0`. Here we assume that the solution was constant before the initial time point. Additionally, we pass
+`constant_lags = c(20.0)` to tell the solver that only constant-time lags were used and what the lag length
+was. This helps improve the solver accuracy by accurately stepping at the points of discontinuity. Together
+this is:
+
+```R
+f <- JuliaCall::julia_eval("function f(du, u, h, p, t)
+ du[1] = 1.1/(1 + sqrt(10)*(h(p, t-20)[1])^(5/4)) - 10*u[1]/(1 + 40*u[2])
+ du[2] = 100*u[1]/(1 + 40*u[2]) - 2.43*u[2]
+end")
+h <- JuliaCall::julia_eval("function h(p, t)
+ [1.05767027/3, 1.030713491/3]
+end")
+u0 <- c(1.05767027/3, 1.030713491/3)
+tspan <- c(0.0, 100.0)
+constant_lags <- c(20.0)
+JuliaCall::julia_assign("u0", u0)
+JuliaCall::julia_assign("tspan", tspan)
+JuliaCall::julia_assign("constant_lags", tspan)
+prob <- JuliaCall::julia_eval("DDEProblem(f, u0, h, tspan, constant_lags = constant_lags)")
+sol <- de$solve(prob,de$MethodOfSteps(de$Tsit5()))
+udf <- as.data.frame(t(sapply(sol$u,identity)))
+plotly::plot_ly(udf, x = sol$t, y = ~V1, type = 'scatter', mode = 'lines') |> plotly::add_trace(y = ~V2)
+```
+
+
+
+Notice that the solver accurately is able to simulate the kink (discontinuity) at `t=20` due to the discontinuity
+of the derivative at the initial time point! This is why declaring discontinuities can enhance the solver accuracy.
+
+## GPU-Accelerated ODE Solving of Ensembles
+
+In many cases one is interested in solving the same ODE many times over many
+different initial conditions and parameters. In diffeqr parlance this is called
+an ensemble solve. diffeqr inherits the parallelism tools of the
+[SciML ecosystem](https://sciml.ai/) that are used for things like
+[automated equation discovery and acceleration](https://arxiv.org/abs/2001.04385).
+Here we will demonstrate using these parallel tools to accelerate the solving
+of an ensemble.
+
+First, let's define the JIT-accelerated Lorenz equation like before:
+
+```R
+de <- diffeqr::diffeq_setup()
+lorenz <- function (u,p,t){
+ du1 = p[1]*(u[2]-u[1])
+ du2 = u[1]*(p[2]-u[3]) - u[2]
+ du3 = u[1]*u[2] - p[3]*u[3]
+ c(du1,du2,du3)
+}
+u0 <- c(1.0,1.0,1.0)
+tspan <- c(0.0,100.0)
+p <- c(10.0,28.0,8/3)
+prob <- de$ODEProblem(lorenz,u0,tspan,p)
+fastprob <- diffeqr::jitoptimize_ode(de,prob)
+```
+
+Now we use the `EnsembleProblem` as defined on the
+[ensemble parallelism page of the documentation](https://diffeq.sciml.ai/stable/features/ensemble/):
+Let's build an ensemble by utilizing uniform random numbers to randomize the
+initial conditions and parameters:
+
+```R
+prob_func <- function (prob,i,rep){
+ de$remake(prob,u0=runif(3)*u0,p=runif(3)*p)
+}
+ensembleprob = de$EnsembleProblem(fastprob, prob_func = prob_func, safetycopy=FALSE)
+```
+
+Now we solve the ensemble in serial:
+
+```R
+sol = de$solve(ensembleprob,de$Tsit5(),de$EnsembleSerial(),trajectories=10000,saveat=0.01)
+```
+
+To add GPUs to the mix, we need to bring in [DiffEqGPU](https://github.com/SciML/DiffEqGPU.jl).
+The `diffeqr::diffeqgpu_setup()` helper function will install CUDA for you and
+bring all of the bindings into the returned object:
+
+```R
+degpu <- diffeqr::diffeqgpu_setup("CUDA")
+```
+
+#### Note: `diffeqr::diffeqgpu_setup` can take awhile to run the first time as it installs the drivers!
+
+Now we simply use `EnsembleGPUKernel(degpu$CUDABackend())` with a
+GPU-specialized ODE solver `GPUTsit5()` to solve 10,000 ODEs on the GPU in
+parallel:
+
+```R
+sol <- de$solve(ensembleprob,degpu$GPUTsit5(),degpu$EnsembleGPUKernel(degpu$CUDABackend()),trajectories=10000,saveat=0.01)
+```
+
+For the full list of choices for specialized GPU solvers, see
+[the DiffEqGPU.jl documentation](https://docs.sciml.ai/DiffEqGPU/stable/manual/ensemblegpukernel/).
+
+Note that `EnsembleGPUArray` can be used as well, like:
+
+```R
+sol <- de$solve(ensembleprob,de$Tsit5(),degpu$EnsembleGPUArray(degpu$CUDABackend()),trajectories=10000,saveat=0.01)
+```
+
+though we highly recommend the `EnsembleGPUKernel` methods for more speed. Given
+the way the JIT compilation performed will also ensure that the faster kernel
+generation methods work, `EnsembleGPUKernel` is almost certainly the
+better choice in most applications.
+
+### Benchmark
+
+To see how much of an effect the parallelism has, let's test this against R's
+deSolve package. This is exactly the same problem as the documentation example
+for deSolve, so let's copy that verbatim and then add a function to do the
+ensemble generation:
+
+```R
+library(deSolve)
+Lorenz <- function(t, state, parameters) {
+ with(as.list(c(state, parameters)), {
+ dX <- a * X + Y * Z
+ dY <- b * (Y - Z)
+ dZ <- -X * Y + c * Y - Z
+ list(c(dX, dY, dZ))
+ })
+}
+
+parameters <- c(a = -8/3, b = -10, c = 28)
+state <- c(X = 1, Y = 1, Z = 1)
+times <- seq(0, 100, by = 0.01)
+out <- ode(y = state, times = times, func = Lorenz, parms = parameters)
+
+lorenz_solve <- function (i){
+ state <- c(X = runif(1), Y = runif(1), Z = runif(1))
+ parameters <- c(a = -8/3 * runif(1), b = -10 * runif(1), c = 28 * runif(1))
+ out <- ode(y = state, times = times, func = Lorenz, parms = parameters)
+}
+```
+
+Using `lapply` to generate the ensemble we get:
+
+```
+> system.time({ lapply(1:1000,lorenz_solve) })
+ user system elapsed
+ 225.81 0.46 226.63
+```
+
+Now let's see how the JIT-accelerated serial Julia version stacks up against that:
+
+```
+> system.time({ de$solve(ensembleprob,de$Tsit5(),de$EnsembleSerial(),trajectories=1000,saveat=0.01) })
+ user system elapsed
+ 2.75 0.30 3.08
+```
+
+Julia is already about 73x faster than the pure R solvers here! Now let's add
+GPU-acceleration to the mix:
+
+```
+> system.time({ de$solve(ensembleprob,degpu$GPUTsit5(),degpu$EnsembleGPUKernel(degpu$CUDABackend()),trajectories=1000,saveat=0.01) })
+ user system elapsed
+ 0.11 0.00 0.12
+```
+
+Already 26x times faster! But the GPU acceleration is made for massively
+parallel problems, so let's up the trajectories a bit. We will not use more
+trajectories from R because that would take too much computing power, so let's
+see what happens to the Julia serial and GPU at 10,000 trajectories:
+
+```
+> system.time({ de$solve(ensembleprob,de$Tsit5(),de$EnsembleSerial(),trajectories=10000,saveat=0.01) })
+ user system elapsed
+ 35.02 4.19 39.25
+```
+
+```
+> system.time({ de$solve(ensembleprob,degpu$GPUTsit5(),degpu$EnsembleGPUKernel(degpu$CUDABackend()),trajectories=10000,saveat=0.01) })
+ user system elapsed
+ 1.22 0.23 1.50
+```
+
+To compare this to the pure Julia code:
+
+```julia
+using OrdinaryDiffEq, DiffEqGPU, CUDA, StaticArrays
+function lorenz(u, p, t)
+ σ = p[1]
+ ρ = p[2]
+ β = p[3]
+ du1 = σ * (u[2] - u[1])
+ du2 = u[1] * (ρ - u[3]) - u[2]
+ du3 = u[1] * u[2] - β * u[3]
+ return SVector{3}(du1, du2, du3)
+end
+
+u0 = SA[1.0f0; 0.0f0; 0.0f0]
+tspan = (0.0f0, 10.0f0)
+p = SA[10.0f0, 28.0f0, 8 / 3.0f0]
+prob = ODEProblem{false}(lorenz, u0, tspan, p)
+prob_func = (prob, i, repeat) -> remake(prob, p = (@SVector rand(Float32, 3)) .* p)
+monteprob = EnsembleProblem(prob, prob_func = prob_func, safetycopy = false)
+@time sol = solve(monteprob, GPUTsit5(), EnsembleGPUKernel(CUDA.CUDABackend()),
+ trajectories = 10_000,
+ saveat = 1.0f0);
+
+# 0.015064 seconds (257.68 k allocations: 13.132 MiB)
+```
+
+which is about two orders of magnitude faster for computing 10,000 trajectories,
+note that the major factors are that we cannot define 32-bit floating point values
+from R and the `prob_func` for generating the initial conditions and parameters
+is a major bottleneck since this function is written in R.
+
+To see how this scales in Julia, let's take it to insane heights. First, let's
+reduce the amount we're saving:
+
+```julia
+@time sol = solve(monteprob,GPUTsit5(),EnsembleGPUKernel(CUDA.CUDABackend()),trajectories=10_000,saveat=1.0f0)
+0.015040 seconds (257.64 k allocations: 13.130 MiB)
+```
+
+This highlights that controlling memory pressure is key with GPU usage: you will
+get much better performance when requiring less saved points on the GPU.
+
+```julia
+@time sol = solve(monteprob,GPUTsit5(),EnsembleGPUKernel(CUDA.CUDABackend()),trajectories=100_000,saveat=1.0f0)
+# 0.150901 seconds (2.60 M allocations: 131.576 MiB)
+```
+
+compared to serial:
+
+```julia
+@time sol = solve(monteprob,Tsit5(),EnsembleSerial(),trajectories=100_000,saveat=1.0f0)
+# 22.136743 seconds (16.40 M allocations: 1.628 GiB, 42.98% gc time)
+```
+
+And now we start to see that scaling power! Let's solve 1 million trajectories:
+
+```julia
+@time sol = solve(monteprob,GPUTsit5(),EnsembleGPUKernel(CUDA.CUDABackend()),trajectories=1_000_000,saveat=1.0f0)
+# 1.031295 seconds (3.40 M allocations: 241.075 MiB)
+```
+
+For reference, let's look at deSolve with the change to only save that much:
+
+```R
+times <- seq(0, 100, by = 1.0)
+lorenz_solve <- function (i){
+ state <- c(X = runif(1), Y = runif(1), Z = runif(1))
+ parameters <- c(a = -8/3 * runif(1), b = -10 * runif(1), c = 28 * runif(1))
+ out <- ode(y = state, times = times, func = Lorenz, parms = parameters)
+}
+
+system.time({ lapply(1:1000,lorenz_solve) })
+```
+
+```
+ user system elapsed
+ 49.69 3.36 53.42
+```
+
+The GPU version is solving 1000x as many trajectories, 50x as fast! So conclusion,
+if you need the most speed, you may want to move to the Julia version to get the
+most out of your GPU due to Float32's, and when using GPUs make sure it's a problem
+with a relatively average or low memory pressure, and these methods will give
+orders of magnitude acceleration compared to what you might be used to.
diff --git a/diffeqr.Rproj b/diffeqr.Rproj
index 08d5ab1..cba1b6b 100644
--- a/diffeqr.Rproj
+++ b/diffeqr.Rproj
@@ -1,21 +1,21 @@
-Version: 1.0
-
-RestoreWorkspace: No
-SaveWorkspace: No
-AlwaysSaveHistory: Default
-
-EnableCodeIndexing: Yes
-UseSpacesForTab: Yes
-NumSpacesForTab: 2
-Encoding: UTF-8
-
-RnwWeave: Sweave
-LaTeX: pdfLaTeX
-
-AutoAppendNewline: Yes
-StripTrailingWhitespace: Yes
-
-BuildType: Package
-PackageUseDevtools: Yes
-PackageInstallArgs: --no-multiarch --with-keep.source
-PackageRoxygenize: rd,collate,namespace
+Version: 1.0
+
+RestoreWorkspace: No
+SaveWorkspace: No
+AlwaysSaveHistory: Default
+
+EnableCodeIndexing: Yes
+UseSpacesForTab: Yes
+NumSpacesForTab: 2
+Encoding: UTF-8
+
+RnwWeave: Sweave
+LaTeX: pdfLaTeX
+
+AutoAppendNewline: Yes
+StripTrailingWhitespace: Yes
+
+BuildType: Package
+PackageUseDevtools: Yes
+PackageInstallArgs: --no-multiarch --with-keep.source
+PackageRoxygenize: rd,collate,namespace
diff --git a/man/diffeqgpu_setup.Rd b/man/diffeqgpu_setup.Rd
index bd4ec04..2308926 100644
--- a/man/diffeqgpu_setup.Rd
+++ b/man/diffeqgpu_setup.Rd
@@ -4,7 +4,10 @@
\alias{diffeqgpu_setup}
\title{Setup DiffEqGPU}
\usage{
-diffeqgpu_setup()
+diffeqgpu_setup(backend)
+}
+\arguments{
+\item{backend}{the backend for the GPU computation. Choices are "CUDA", "AMDGPU", "Metal", or "oneAPI"}
}
\description{
This function initializes the DiffEqGPU package for GPU-parallelized ensembles.
@@ -12,14 +15,14 @@ The first time will be long since it includes precompilation.
}
\value{
Returns a degpu object which holds the module state of the Julia-side DiffEqGPU
- package. The core use is to use degpu$EnsembleGPUArray() for choosing the GPU
+ package. The core use is to use degpu$EnsembleGPUKernel() for choosing the GPU
dispatch in the solve.
}
\examples{
\dontrun{ ## diffeqgpu_setup() is time-consuming and requires Julia+DifferentialEquations.jl
-degpu <- diffeqr::diffeqgpu_setup()
+degpu <- diffeqr::diffeqgpu_setup(backend)
}
diff --git a/vignettes/gpu.Rmd b/vignettes/gpu.Rmd
index 2801fd5..7438469 100644
--- a/vignettes/gpu.Rmd
+++ b/vignettes/gpu.Rmd
@@ -16,11 +16,9 @@ knitr::opts_chunk$set(
)
```
-## GPU-Accelerated ODE Solving of Ensembles
-
In many cases one is interested in solving the same ODE many times over many
different initial conditions and parameters. In diffeqr parlance this is called
-an ensemble solve. diffeqr inherits the parallelism tools of the
+an ensemble solve. diffeqr inherits the parallelism tools of the
[SciML ecosystem](https://sciml.ai/) that are used for things like
[automated equation discovery and acceleration](https://arxiv.org/abs/2001.04385).
Here we will demonstrate using these parallel tools to accelerate the solving
@@ -43,7 +41,7 @@ prob <- de$ODEProblem(lorenz,u0,tspan,p)
fastprob <- diffeqr::jitoptimize_ode(de,prob)
```
-Now we use the `EnsembleProblem` as defined on the
+Now we use the `EnsembleProblem` as defined on the
[ensemble parallelism page of the documentation](https://diffeq.sciml.ai/stable/features/ensemble/):
Let's build an ensemble by utilizing uniform random numbers to randomize the
initial conditions and parameters:
@@ -66,15 +64,33 @@ The `diffeqr::diffeqgpu_setup()` helper function will install CUDA for you and
bring all of the bindings into the returned object:
```R
-degpu <- diffeqr::diffeqgpu_setup()
+degpu <- diffeqr::diffeqgpu_setup("CUDA")
+```
+
+#### Note: `diffeqr::diffeqgpu_setup` can take awhile to run the first time as it installs the drivers!
+
+Now we simply use `EnsembleGPUKernel(degpu$CUDABackend())` with a
+GPU-specialized ODE solver `GPUTsit5()` to solve 10,000 ODEs on the GPU in
+parallel:
+
+```R
+sol <- de$solve(ensembleprob,degpu$GPUTsit5(),degpu$EnsembleGPUKernel(degpu$CUDABackend()),trajectories=10000,saveat=0.01)
```
-Now we simply use `EnsembleGPUArray()` to solve 10,000 ODEs on the GPU in parallel:
+For the full list of choices for specialized GPU solvers, see
+[the DiffEqGPU.jl documentation](https://docs.sciml.ai/DiffEqGPU/stable/manual/ensemblegpukernel/).
+
+Note that `EnsembleGPUArray` can be used as well, like:
```R
-sol <- de$solve(ensembleprob,de$Tsit5(),degpu$EnsembleGPUArray(),trajectories=10000,saveat=0.01)
+sol <- de$solve(ensembleprob,de$Tsit5(),degpu$EnsembleGPUArray(degpu$CUDABackend()),trajectories=10000,saveat=0.01)
```
+though we highly recommend the `EnsembleGPUKernel` methods for more speed. Given
+the way the JIT compilation performed will also ensure that the faster kernel
+generation methods work, `EnsembleGPUKernel` is almost certainly the
+better choice in most applications.
+
### Benchmark
To see how much of an effect the parallelism has, let's test this against R's
@@ -109,7 +125,7 @@ Using `lapply` to generate the ensemble we get:
```
> system.time({ lapply(1:1000,lorenz_solve) })
- user system elapsed
+ user system elapsed
225.81 0.46 226.63
```
@@ -117,61 +133,64 @@ Now let's see how the JIT-accelerated serial Julia version stacks up against tha
```
> system.time({ de$solve(ensembleprob,de$Tsit5(),de$EnsembleSerial(),trajectories=1000,saveat=0.01) })
- user system elapsed
- 2.75 0.30 3.08
+ user system elapsed
+ 2.75 0.30 3.08
```
Julia is already about 73x faster than the pure R solvers here! Now let's add
GPU-acceleration to the mix:
```
-> system.time({ de$solve(ensembleprob,de$Tsit5(),degpu$EnsembleGPUArray(),trajectories=1000,saveat=0.01) })
+> system.time({ de$solve(ensembleprob,degpu$GPUTsit5(),degpu$EnsembleGPUKernel(degpu$CUDABackend()),trajectories=1000,saveat=0.01) })
user system elapsed
- 1.33 1.57 2.93
+ 0.11 0.00 0.12
```
-That's only around 2x faster. But the GPU acceleartion is made for massively
+Already 26x times faster! But the GPU acceleration is made for massively
parallel problems, so let's up the trajectories a bit. We will not use more
trajectories from R because that would take too much computing power, so let's
see what happens to the Julia serial and GPU at 10,000 trajectories:
```
> system.time({ de$solve(ensembleprob,de$Tsit5(),de$EnsembleSerial(),trajectories=10000,saveat=0.01) })
- user system elapsed
- 35.02 4.19 39.25
+ user system elapsed
+ 35.02 4.19 39.25
```
```
-> system.time({ de$solve(ensembleprob,de$Tsit5(),degpu$EnsembleGPUArray(),trajectories=10000,saveat=0.01) })
+> system.time({ de$solve(ensembleprob,degpu$GPUTsit5(),degpu$EnsembleGPUKernel(degpu$CUDABackend()),trajectories=10000,saveat=0.01) })
user system elapsed
- 12.03 3.57 15.60
+ 1.22 0.23 1.50
```
To compare this to the pure Julia code:
```julia
-using OrdinaryDiffEq, DiffEqGPU
-function lorenz(du,u,p,t)
- @inbounds begin
- du[1] = p[1]*(u[2]-u[1])
- du[2] = u[1]*(p[2]-u[3]) - u[2]
- du[3] = u[1]*u[2] - p[3]*u[3]
- end
- nothing
+using OrdinaryDiffEq, DiffEqGPU, CUDA, StaticArrays
+function lorenz(u, p, t)
+ σ = p[1]
+ ρ = p[2]
+ β = p[3]
+ du1 = σ * (u[2] - u[1])
+ du2 = u[1] * (ρ - u[3]) - u[2]
+ du3 = u[1] * u[2] - β * u[3]
+ return SVector{3}(du1, du2, du3)
end
-u0 = Float32[1.0;1.0;1.0]
-tspan = (0.0f0,100.0f0)
-p = [10.0f0,28.0f0,8/3f0]
-prob = ODEProblem(lorenz,u0,tspan,p)
-prob_func = (prob,i,repeat) -> remake(prob,u0=rand(Float32,3).*u0,p=rand(Float32,3).*p)
-monteprob = EnsembleProblem(prob, prob_func = prob_func, safetycopy=false)
-@time sol = solve(monteprob,Tsit5(),EnsembleGPUArray(),trajectories=10_000,saveat=0.01f0)
+u0 = SA[1.0f0; 0.0f0; 0.0f0]
+tspan = (0.0f0, 10.0f0)
+p = SA[10.0f0, 28.0f0, 8 / 3.0f0]
+prob = ODEProblem{false}(lorenz, u0, tspan, p)
+prob_func = (prob, i, repeat) -> remake(prob, p = (@SVector rand(Float32, 3)) .* p)
+monteprob = EnsembleProblem(prob, prob_func = prob_func, safetycopy = false)
+@time sol = solve(monteprob, GPUTsit5(), EnsembleGPUKernel(CUDA.CUDABackend()),
+ trajectories = 10_000,
+ saveat = 1.0f0);
-# 9.444439 seconds (22.96 M allocations: 6.464 GiB, 44.53% gc time)
+# 0.015064 seconds (257.68 k allocations: 13.132 MiB)
```
-which is more than an order of magnitude faster for computing 10,000 trajectories,
+which is about two orders of magnitude faster for computing 10,000 trajectories,
note that the major factors are that we cannot define 32-bit floating point values
from R and the `prob_func` for generating the initial conditions and parameters
is a major bottleneck since this function is written in R.
@@ -180,16 +199,16 @@ To see how this scales in Julia, let's take it to insane heights. First, let's
reduce the amount we're saving:
```julia
-@time sol = solve(monteprob,Tsit5(),EnsembleGPUArray(),trajectories=10_000,saveat=1.0f0)
-# 0.801215 seconds (1.66 M allocations: 133.846 MiB)
+@time sol = solve(monteprob,GPUTsit5(),EnsembleGPUKernel(CUDA.CUDABackend()),trajectories=10_000,saveat=1.0f0)
+0.015040 seconds (257.64 k allocations: 13.130 MiB)
```
This highlights that controlling memory pressure is key with GPU usage: you will
get much better performance when requiring less saved points on the GPU.
```julia
-@time sol = solve(monteprob,Tsit5(),EnsembleGPUArray(),trajectories=100_000,saveat=1.0f0)
-# 1.871536 seconds (6.66 M allocations: 919.521 MiB, 2.48% gc time)
+@time sol = solve(monteprob,GPUTsit5(),EnsembleGPUKernel(CUDA.CUDABackend()),trajectories=100_000,saveat=1.0f0)
+# 0.150901 seconds (2.60 M allocations: 131.576 MiB)
```
compared to serial:
@@ -202,8 +221,8 @@ compared to serial:
And now we start to see that scaling power! Let's solve 1 million trajectories:
```julia
-@time sol = solve(monteprob,Tsit5(),EnsembleGPUArray(),trajectories=1_000_000,saveat=1.0f0)
-# 25.234710 seconds (56.53 M allocations: 8.579 GiB, 51.61% gc time)
+@time sol = solve(monteprob,GPUTsit5(),EnsembleGPUKernel(CUDA.CUDABackend()),trajectories=1_000_000,saveat=1.0f0)
+# 1.031295 seconds (3.40 M allocations: 241.075 MiB)
```
For reference, let's look at deSolve with the change to only save that much:
@@ -219,7 +238,12 @@ lorenz_solve <- function (i){
system.time({ lapply(1:1000,lorenz_solve) })
```
-The GPU version is solving 1000x as many trajectories, 2x as fast! So conclusion,
+```
+ user system elapsed
+ 49.69 3.36 53.42
+```
+
+The GPU version is solving 1000x as many trajectories, 50x as fast! So conclusion,
if you need the most speed, you may want to move to the Julia version to get the
most out of your GPU due to Float32's, and when using GPUs make sure it's a problem
with a relatively average or low memory pressure, and these methods will give