密码学系列之:blowfish对称密钥分组算法
Blowfish是由Bruce Schneier在1993年发明的对称密钥分组加密算法,类似的DES和AES都是分组加密算法,Blowfish是用来替代DES算法出现的,并且Blowfish是没有商用限制的,任何人都可以自由使用。
对比而言,虽然AES也是一种密码强度很高的对称密码算法,但是如果需要商用的话要向NIST支付授权费用。
blowfish和DES一样,使用的是feistel密码来进行分组加密。blowfish的分组块大小是64bits,可变密钥长度可以从32bits到448bits不等。
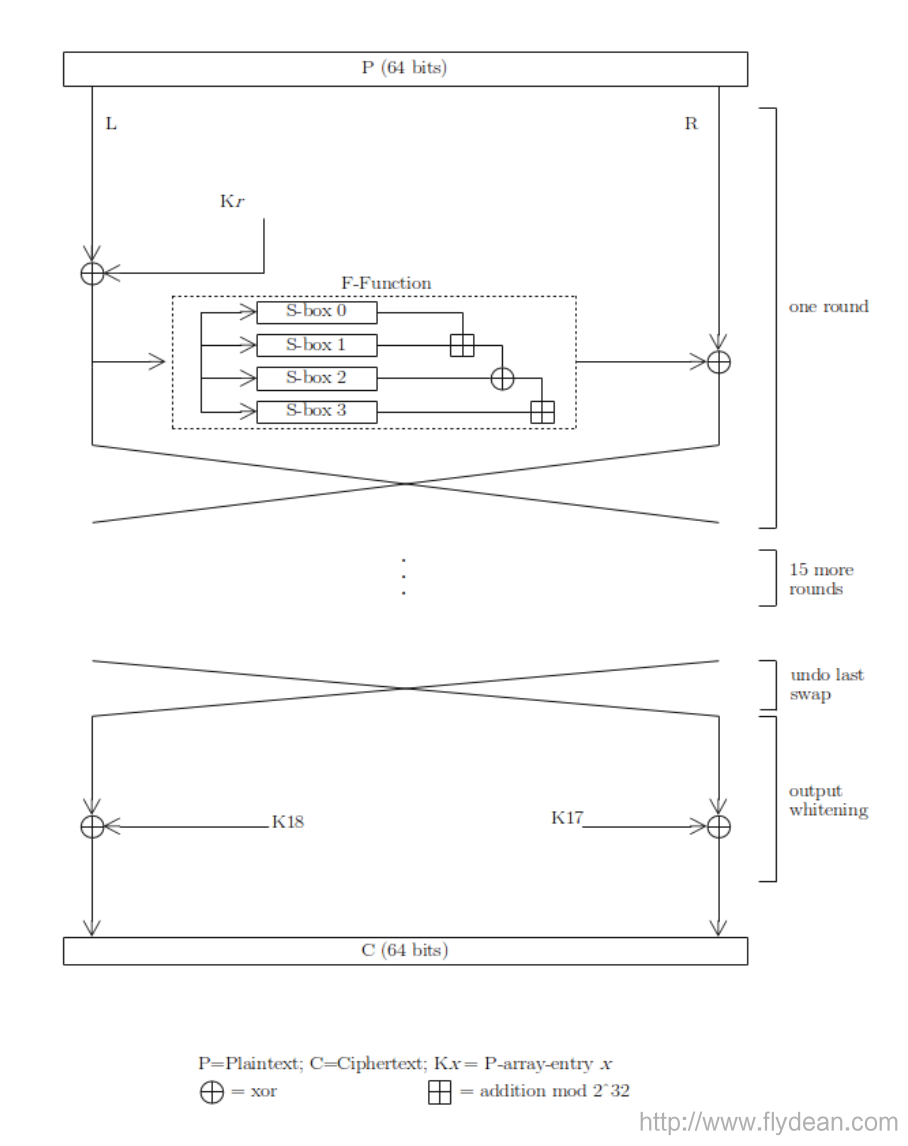
blowfish需要进行16轮的feistel加密操作,我们先从下图大致感受一下blowfish算法的加密流程:
大概的流程就是将P(原始数据)分成左右两部分,先拿左边的部分和Kr 做异或操作,得出的结果调用F函数,最后将F函数的输出结果和右半部分进行异或操作。
调换左右部分的位置,继续进行这样的操作,总共进行16轮就得到了最终的加密结果。
大家可以看到整个加密过程中最重要的两个变量就是Kr 和 F函数。
接下来我们会详细进行讲解。
从图上我们可以看到,Kr 的范围是从K1 到 K18 。总共有18个密钥组成的数组。 每个密钥的长度是32位。
我们来看一下密钥数组是怎么生成的。
首先我们使用随机数来对密钥数组进行初始化。怎么才能生成一个足够随机的32位数字呢?
一个很常用的方法就是使用常量π的小数部分,将其转换成为16净值,如下所示:
K1 = 0x76a301d3
K2 = 0xbc452aef
...
K18 = 0xd7acc4a5
还记得blowfish的可变密钥的长度吗?是从32bits到448bits,也就是从1到14个32位的数字。我们用Pi来表示,那么就是从P1到P14总共14个可变密钥。
接下来我们需要使用K和P进行操作,从而生成最终的K数组。
我们使用K1和P1进行异或操作,K2和P2进行异或操作,一直到K14和P14。
因为P只有14个值,而K有18个值,所以接下来我们需要重复使用P的值,也就是K15和P1进行异或,K16和P2进行异或,直到K18和P4。
将异或之后的值作为新的K数组的值。
现在我们获得了一个新的K数组。
注意,这个K数组并不是最终的数组,我们接下来看。
在生成最终的P数组之前,我们还要介绍一个概念叫做S-box。
在密码学中,s-box的全称是substitution-box,也就是一个替换盒子,可以将输入替换成不同的输出。
S-box 接收 n个bits的输入,然后将其转换成m个bits的输出。
这里n和m可以是不等的。
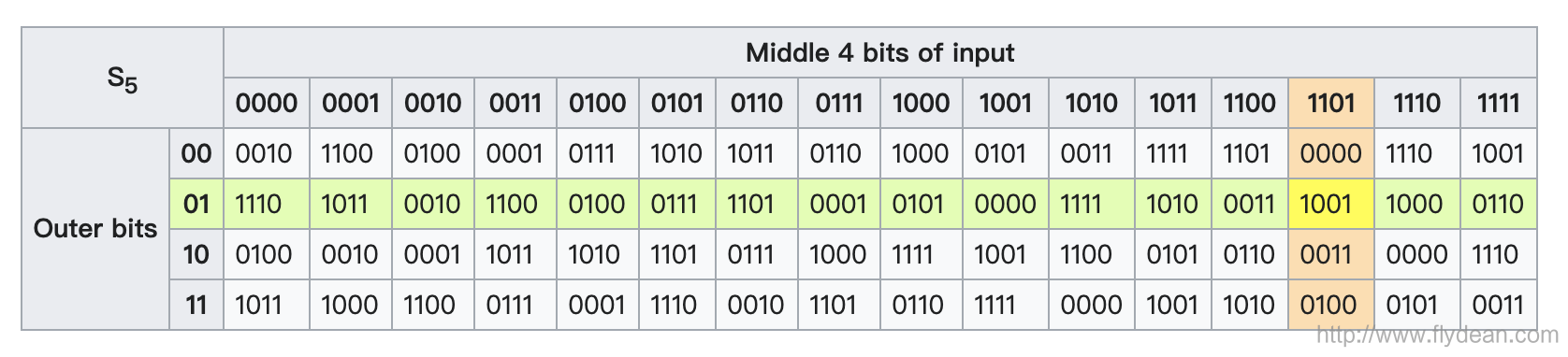
我们看一下DES中S-box的例子:
上面的S-box将6-bits的输入转换成为4-bits的输出。
S-box可以是固定的,也可以是动态的。比如,在DES中S-box就是静态的,而在Blowfish和Twofish中S-box就是动态生成的。
Blowfish算法中的F函数需要用到4个S-box,F函数的输入是32bits,首先将32bits分成4份,也就是4个8bits。
S-box的作用就是将8bits转换成为32bits。
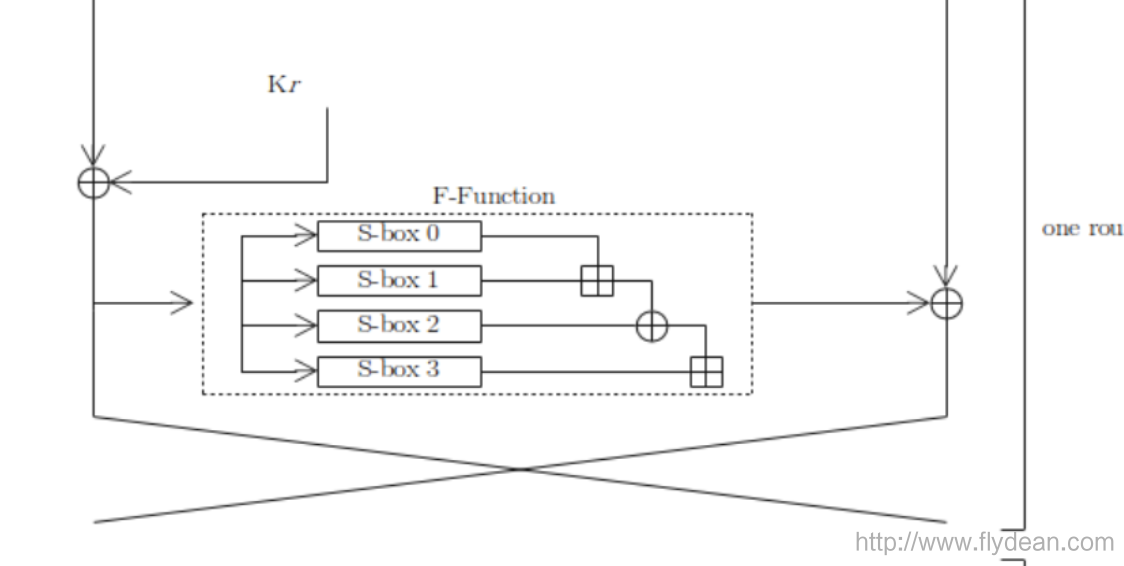
我们再详细看一下F函数的工作流程:
S-box生成的值会进行相加,然后进行异或操作。最终得到最终的32bits。
S-box的初始值也可以跟K数组一样,使用常量π的小数部分来初始化。
在上面两节,我们生成了初始化的K数组和S-box。
blowfish认为这样还不够安全,不够随机。
我们还需要进行一些操作来生成最终的K数组。
首先我们取一个全为0的64bits,然后K数组和S-box,应用blowfish算法,生成一个64bits。
将这个64bits分成两部分,分别作为新的K1 和 K2。
然后将这个64bits作为输入,再次调用blowfish算法,作为新的K3 和 K4。
依次类推,最终生成所有K数组中的元素。
4个S-box的数组也按照上面的流程来进行生成。从而得到最终的S-box。
有了最终的K数组和S-box,我们就可以真正的对要加密的文件进行加密操作了。
用个伪代码来表示整个流程:
uint32_t P[18];
uint32_t S[4][256];
uint32_t f (uint32_t x) {
uint32_t h = S[0][x >> 24] + S[1][x >> 16 & 0xff];
return ( h ^ S[2][x >> 8 & 0xff] ) + S[3][x & 0xff];
}
void encrypt (uint32_t & L, uint32_t & R) {
for (int i=0 ; i<16 ; i += 2) {
L ^= P[i];
R ^= f(L);
R ^= P[i+1];
L ^= f(R);
}
L ^= P[16];
R ^= P[17];
swap (L, R);
}
void decrypt (uint32_t & L, uint32_t & R) {
for (int i=16 ; i > 0 ; i -= 2) {
L ^= P[i+1];
R ^= f(L);
R ^= P[i];
L ^= f(R);
}
L ^= P[1];
R ^= P[0];
swap (L, R);
}
// ...
// initializing the P-array and S-boxes with values derived from pi; omitted in the example
// ...
{
for (int i=0 ; i<18 ; ++i)
P[i] ^= key[i % keylen];
uint32_t L = 0, R = 0;
for (int i=0 ; i<18 ; i+=2) {
encrypt (L, R);
P[i] = L; P[i+1] = R;
}
for (int i=0 ; i<4 ; ++i)
for (int j=0 ; j<256; j+=2) {
encrypt (L, R);
S[i][j] = L; S[i][j+1] = R;
}
}从上面的流程可以看出,blowfish在生成最终的K数组和S-box需要耗费一定的时间,但是一旦生成完毕,或者说密钥不变的情况下,blowfish还是很快速的一种分组加密方法。
每个新的密钥都需要进行大概4 KB文本的预处理,和其他分组密码算法相比,这个会很慢。
那么慢有没有好处呢?
当然有,因为对于一个正常应用来说,是不会经常更换密钥的。所以预处理只会生成一次。在后面使用的时候就会很快了。
而对于恶意攻击者来说,每次尝试新的密钥都需要进行漫长的预处理,所以对攻击者来说要破解blowfish算法是非常不划算的。所以blowfish是可以抵御字典攻击的。
因为blowfish没有任何专利限制,任何人都可以免费使用。这种好处促进了它在密码软件中的普及。
比如使用blowfish的bcrypt算法,我们会在后面的文章中进行讲解。
Blowfish使用64位块大小(与AES的128位块大小相比)使它容易受到生日攻击,特别是在HTTPS这样的环境中。 2016年,SWEET32攻击演示了如何利用生日攻击对64位块大小的密码执行纯文本恢复(即解密密文)。
因为blowfish的块只有64bits,比较小,所以GnuPG项目建议不要使用Blowfish来加密大于4 GB的文件。
除此之外,Blowfish如果只进行一轮加密的话,容易受到反射性弱键的已知明文攻击。 但是我们的实现中使用的是16轮加密,所以不容易受到这种攻击。但是Blowfish的发明人布鲁斯·施耐尔(Bruce Schneier)还是建议大家迁移到Blowfish的继承者Twofish去。
本文已收录于 www.flydean.com
最通俗的解读,最深刻的干货,最简洁的教程,众多你不知道的小技巧等你来发现!
欢迎关注我的公众号:「程序那些事」,懂技术,更懂你!