看动画学算法之:递归和递归树
在之前我们介绍的很多数据结构和算法都用到了递归,递归非常容易理解,用途也很广泛,但是有一个缺点就是需要保存栈的状态,如果递归次数太多会造成栈溢出的问题。
本文将会讲解常见的栈的应用,并使用递归树形象的展示其递归的过程。
递归树是迭代过程的一种图像表述。递归树往往被用于求解递归方程, 它的求解表示比一般的迭代会更加的简洁与清晰。
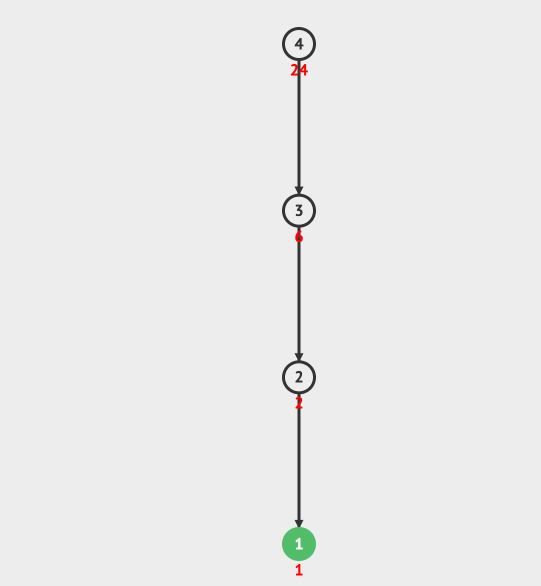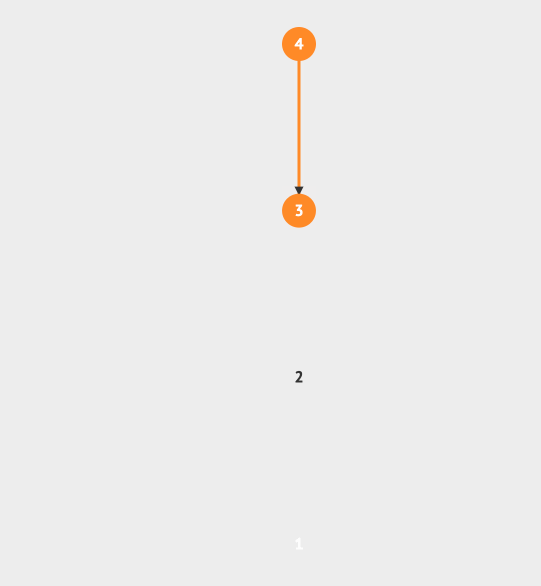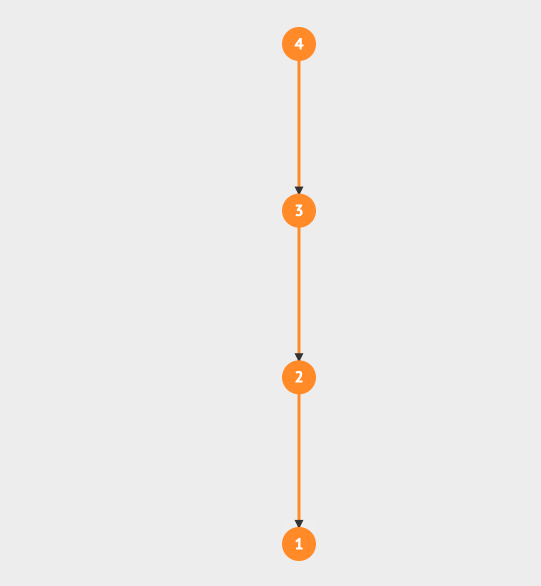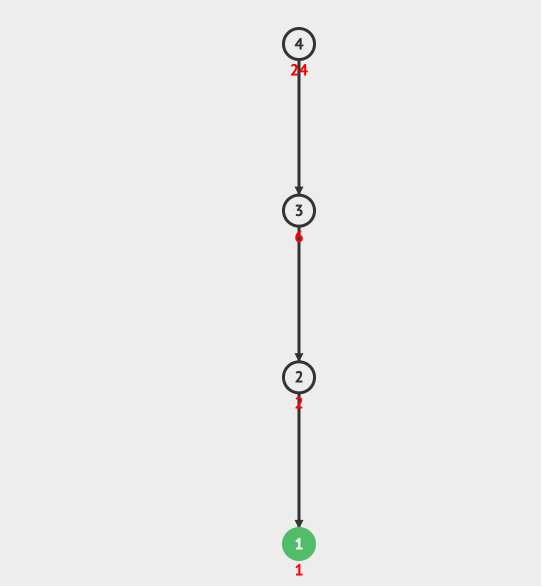
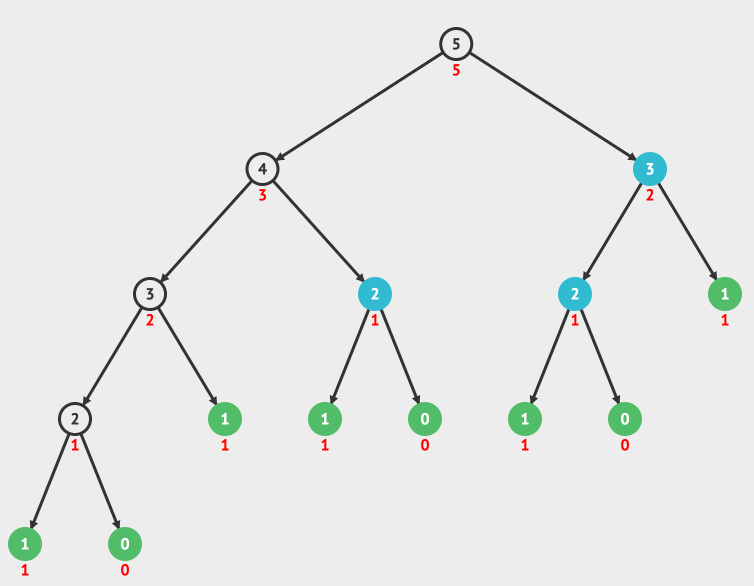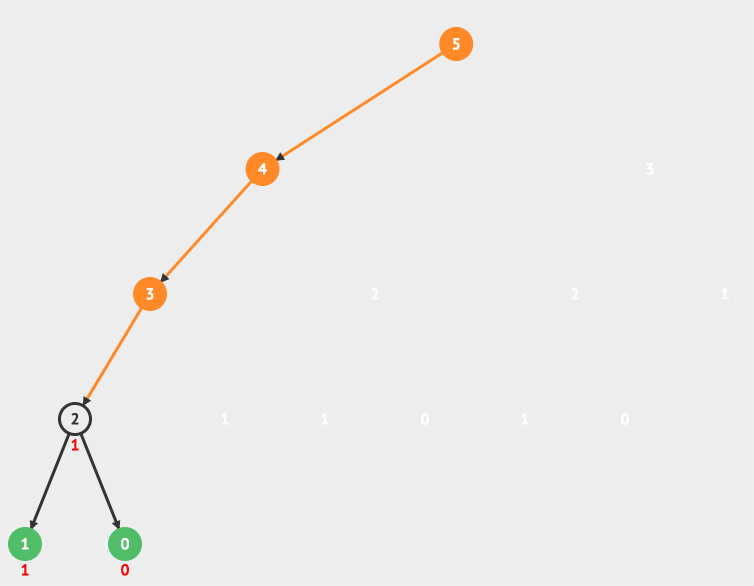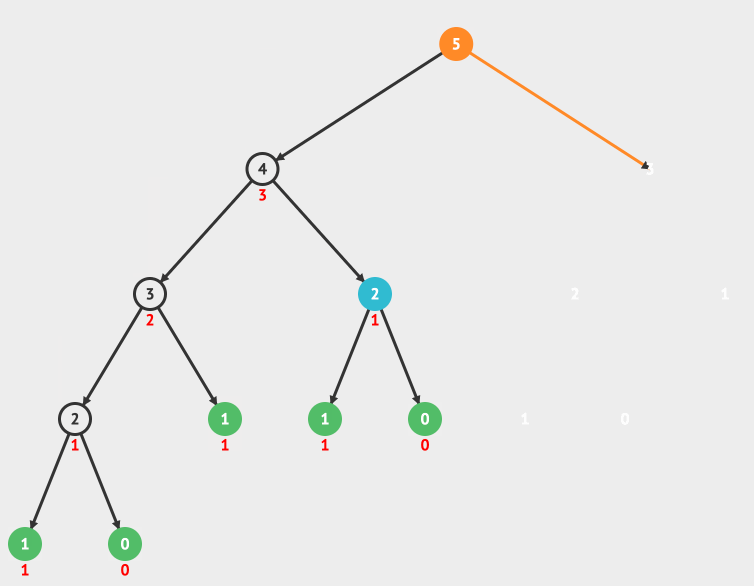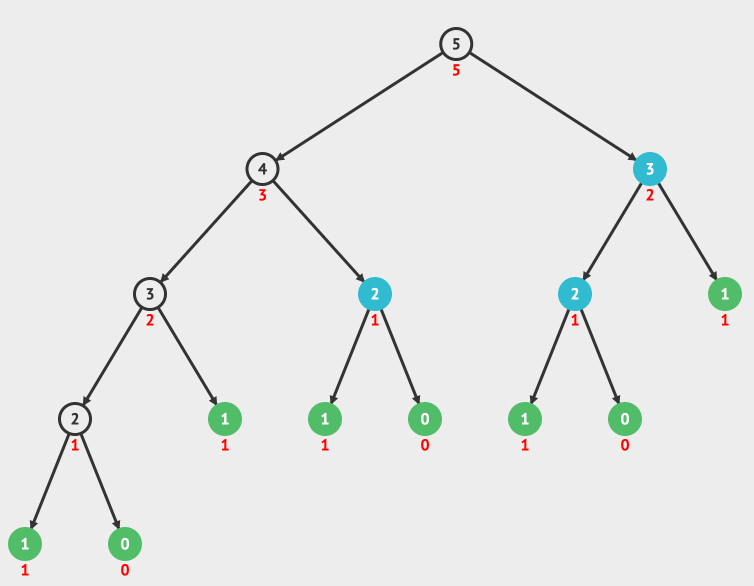
看一个最简单的使用递归的例子,就是阶乘。
比如 4!=4* 3!= 4 * 3 * 2! = 4 * 3 * 2 * 1! =24。
我们用一个动画来详细看一下阶乘的递归调用和它的递归树。
递归树的运行过程是先构建递归树,然后从最底层得到运行结果,一层一层的进行回归,最后得到最终的结果。
我们看下阶乘的java实现是怎么样的:
public int f(int n){
if (n <= 1) /* base case */
return 1;
else /* recursive case */
return n*f(n-1);
}斐波那契数列(Fibonacci sequence)也是一个使用递归的非常常见的例子。
斐波那契数列的数学表达式是:F(1)=1,F(2)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 3,n ∈ N*)
这个例子用递归来怎么写呢?
public int f(int n){
if (n <= 1) /* base case */
return n;
else /* recursive caseS */
return f(n-1) + f(n-2);
}看下递归树的动画:
两个正整数a和b(a>b),它们的最大公约数等于a除以b的余数c和b之间的最大公约数。
代码举例:
public int f(int a, int b){
if (b == 0) /* base case */
return a;
else /* recursive case */
return f(b, a%b);
}N个数中选K个有几种选法呢?
考虑特殊的情况,当K=0的时候,有一种选法。当K=N的时候,也只有一种选法。
而从N中选K,可以分成两部分,假设N个数中有一个X,那么N中选K就可以分为两部分,第一部分是包含X的选法,第二部分是不包含X的选法。
如果包含X,那么就是从剩下的N-1中选择K-1,如果不包含X,那么就是从剩下的N-1中选择K。
这样我们的递归算法就出来了:
public int f(int n, int k){
if (k == 0 || k == n) /* base caseS */
return 1;
else /* recursive caseS */
return f(n-1, k-1) + /* take */
f(n-1, k); /* not take */
}0-1背包问题说的是,我们的背包能够承受一定的重量packageWeight,然后可以向背包里面放入k个物品,每个物品都有独自的重量和价值,我们希望找到价值最大的那种放法。
怎么解决这个问题呢?
我们可以假设一下,我们用函数f来表示到第i个元素的时候,背包最大承重w的最优解为f(i,w),那么在选择是否放入第i个物品的时候,前面的i-1个物品,肯定已经达到了最优解。
如果选择放入第i个元素,i个元素的最优解就是f(i-1,w-weights[i])+values[i],如果选择不放入第i个元素,那么前i-1个元素的最优解就是f(i-1,w)。
我们只需要判断这两个最优解谁大就行了。
再考虑一下边界条件,我们可以得到下面的公式:
我们的代码可以这样写:
/**
*
* @param count 背包中的元素个数
* @param packageWeight 背包能够容纳的总重量
* @return
*/
public int f (int count, int packageWeight){
int[] values= new int[]{100, 70, 50, 10};
int[] weights=new int[]{10, 4, 6, 12};
/* base caseS */
if (packageWeight == 0 || count < 0) return 0;
else if (weights[count] > packageWeight) return f(count-1, packageWeight);
return Math.max(
values[count] + f(count-1, packageWeight-weights[count]), /* take */
f(count-1, packageWeight)); /* not take */
}硬币找零问题就是当硬币种类为 [0 …,… index] 种,兑换金额为 v 时,最少的硬币数量。
怎么解决这个问题呢?
假如硬币的面值分别是coin[1,3,4,5],假如我们的兑换金额是v,用函数来表示coin的最小个数就是f(v)。
同样的,假设我们在新放入硬币之前,系统已经达到了最优解,现在有两种情况:
1种是需要放入新的硬币,那么最小个数就是1 + f(v-coin[i]),1种是不需要放入新的硬币,那么最小的个数就是之前的值不变。
我们只需要取这两种情况的值的最小值即可。
为了方便起见,我们可以设置f(v)的初始返回值是99。
public int f(int v){
int[] coins = new int[]{1,3,4,5};
if (v == 0) return 0; /* base case */
/* recursive caseS */
var ans = 99; //设置一个最大值
for (var i = 0; i < 4; i++)
if (v-coins[i] >= 0)
ans = Math.min(ans, 1 + f(v-coins[i]));
return ans;
}数组的最长递增子序列指的是,给定一个数组,找出数组中最长的递增子数组长度。注意,这里并不要求子数组是连续排列的,只需要递增即可。
比如:给定数组[-7,10,9,2,3,8,8,1], 我们需要找index = 5的数组中递增子数组,那么就是[-7,2,3,8],其长度为4.
怎么解决这个问题呢?
我们可以假设递增子数组的初始长度为1,假如现在我们已经得到了index=4的递增子数组长度为f(4)。
那么当index增加1,也就是index=5的时候,如果number[index]比number[0-(index-1)]间的所有的数都小,则不满足递增子序列的条件,返回值不做处理,保持原值。
如果number[index]比number[0-(index-1)]间的某些数要大,则比较原值和f(j)+1中的最大值。
相应的代码如下:
public int f(int i){
int[] numbers = new int[]{-7,10,9,2,3,8,8,1};
if (i == 0) return 1; /* base case */
/* recursive caseS */
var ans = 1;
for (var j = 0; j < i; j++)
if (numbers[j] < numbers[i])
ans = Math.max(ans, f(j)+1);
return ans;
}旅行商问题要解决的是,一个售货员必须访问n个城市,恰好访问每个城市一次,并最终回到出发城市,求最短的路径和。
假如我们有4个城市,我们用一个二维数组来表示到每个城市的路径:
[[0, 20, 42, 35], [20, 0, 30, 34], [42, 30, 0, 12], [35, 34, 12, 0]]
上面我们有4个城市,分别用0,1,2,3来表示。
我们用m表示要经过的城市顶点集合,那么从城市0到其他城市的最短路径长度,就可以表示为f(0,m)。
假如我们用C01表示城市0和1之间的路径,C02表示城市0和2之间的路径,那么:
那么f(0,{1,2,3}) = min {C01+ f(1,{2,3}), C02+ f(2,{1,3}), C03+ f(3,{1,2})}
一直递归下去就行了,直到最后只剩一个节点。
那么我们怎么来表示要经过的城市顶点集合m呢?
考虑下,我们现在有4个城市,如果每个城市用二进制来表示的话,我们可以用0000来表示0,1,2,3这四个城市,用0001来表示1,2,3这三个城市。
也就是说0表示城市存在,1表示城市不存在。
那么我们的代码可以这样写:
public int f(int u, int m){
int[][] arrays = new int[][]{{0, 20, 42, 35}, {20, 0, 30, 34}, {42, 30, 0, 12}, {35, 34, 12, 0}};
if (m == (1<<4)-1) return arrays[u][0];
var ans = 99; /* recursive caseS */
for (var v = 0; v < 4; v++)
if (v != u && ((m & (1<<v)) == 0))
ans = Math.min(ans, arrays[u][v] + f(v, m | (1<<v)));
return ans;
}当m == (1<<4)-1 也就是1111的时候,表示所有城市都遍历了,直接返回index=0的值即可。
在遍历的时候,我们需要判断一下v和u是否相等,因为相等表示的是同一个城市,不需要进行计算。
同时我们需要判断城市v是否在m中存在,存在我们才继续下一步操作。
最后我们在比较最小值的时候,需要从m中剔除v这个城市。
运行f(0,1)=97。
本文的代码地址:
本文收录于 www.flydean.com
最通俗的解读,最深刻的干货,最简洁的教程,众多你不知道的小技巧等你来发现!
欢迎关注我的公众号:「程序那些事」,懂技术,更懂你!