看动画学算法之:排序-count排序
今天我们介绍一种不需要作比较就能排序的算法:count排序。
count排序是一种空间换时间的算法,我们借助一个外部的count数组来统计各个元素出现的次数,从而最终完成排序。
count排序有一定的限制,因为外部的count数组长度是和原数组的元素范围是一致的,所以count排序一般只适合数组中元素范围比较小的情况。
我们举一个0-9的元素的排序的例子:3,4,2,5,6,2,4,9,1,3,5。
先看一个动画,看看是怎么排序的:
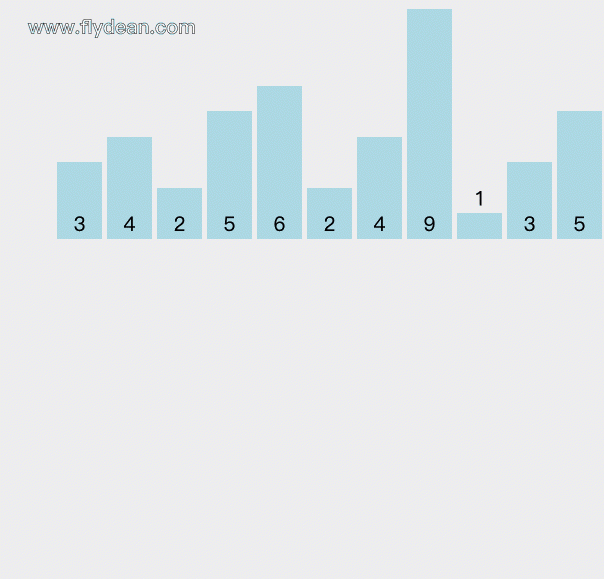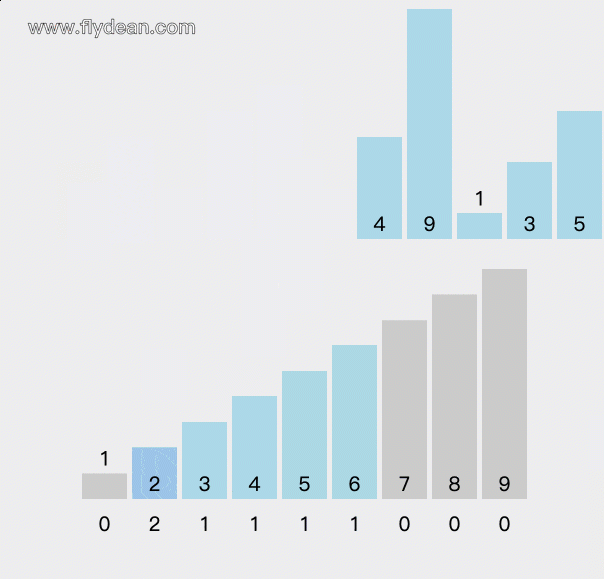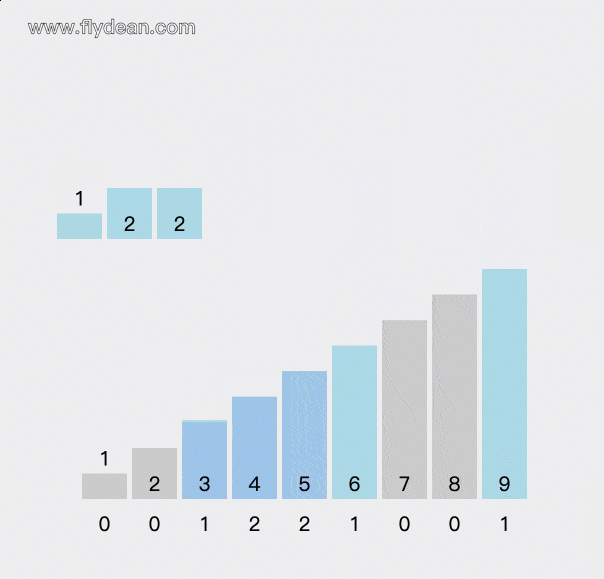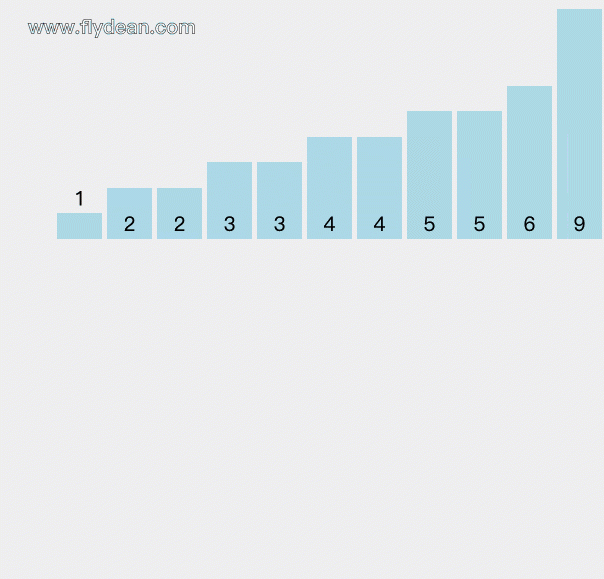
count数组里面存放的是从0到9这些元素出现的次数。
我们遍历原始数组,遇到相应的数字就给相应的count+1。
等所有的元素都count之后,再根据count数组中的值还原排序过后的数组。
count排序很简单,我们主要掌握下面两个大的步骤:
- 遍历原始数组,构建count数组。
- 根据count数组中的count值,重新构建排序数组。
public class CountingSort {
public void doCountingSort(int[] array){
int n = array.length;
// 存储排序过后的数组
int output[] = new int[n];
// count数组,用来存储统计各个元素出现的次数
int count[] = new int[10];
for (int i=0; i<10; ++i) {
count[i] = 0;
}
log.info("初始化count值:{}",count);
// 将原始数组中数据出现次数存入count数组
for (int i=0; i<n; ++i) {
++count[array[i]];
}
log.info("count之后count值:{}",count);
//遍历count,将相应的数据插入output
int j=0;
for(int i=0; i<10; i++){
while(count[i]-- > 0){
output[j++]=i;
}
}
log.info("构建output之后的output值:{}",output);
//将排序后的数组写回原数组
for (int i = 0; i<n; ++i)
array[i] = output[i];
}
public static void main(String[] args) {
int[] array= {3,4,2,5,6,2,4,9,1,3,5};
CountingSort countingSort=new CountingSort();
log.info("countingSort之前的数组为:{}",array);
countingSort.doCountingSort(array);
}
}上面的注释应该很清楚了。
运行的结果如下:
在我们获得count数组中每个元素的个数之后,其实我们还有另外一个生成结果数组的办法:
// 这里是一个小技巧,我们根据count中元素出现的次数计算对应元素第一次应该出现在output中的下标。
//这里的下标是从右往左数的
for (int i=1; i<10; i++) {
count[i] += count[i - 1];
}
log.info("整理count对应的output下标:{}",count);
// 根据count中的下标,构建排序后的数组
//插入一个之后,相应的count下标要减一
for (int i = n-1; i>=0; i--)
{
output[count[array[i]]-1] = array[i];
--count[array[i]];
}
log.info("构建output之后的output值:{}",output);主要分为两步:
第一步我们根据count中元素出现的次数计算对应元素第一次应该出现在output中的下标。这里的下标是从右往左数的。
第二步根据count中的下标,构建排序后的数组,插入一个之后,相应的count下标要减一。
可能不是很好理解,大家可以结合输出结果反复琢磨一下。
从上面的代码我们可以看到,count排序实际上只做了少量次数的遍历。所以它的时间复杂度是O(n)。
本文的代码地址:
本文已收录于 www.flydean.com
最通俗的解读,最深刻的干货,最简洁的教程,众多你不知道的小技巧等你来发现!
欢迎关注我的公众号:「程序那些事」,懂技术,更懂你!