PQ 树是一种基于树的数据结构,代表一组元素上的一系列排列,由 Kellogg S. Booth 和 George S. Lueker 于 1976 年发现命名,用来解决以下问题
给出
$m$ 个集合$S_i$ ,你要找到一个$1\sim n$ 的排列,使得每个集合内的元素都相邻。
PQ 树可以在
PQ 树有三种结点:叶子结点、P 结点 和 Q 结点。其中叶子结点代表排列中的一个元素,P 结点表示它的子结点可以任意排列,Q 结点表示它的儿子顺序可以反转。所有非叶子结点都是 P 结点或 Q 结点中的一种。P 结点至少有 2 个儿子,Q 结点至少有 3 个儿子。
由于结点的定义,PQ 树本身代表了 所有的 合法方案,其先序遍历就是其中之一。
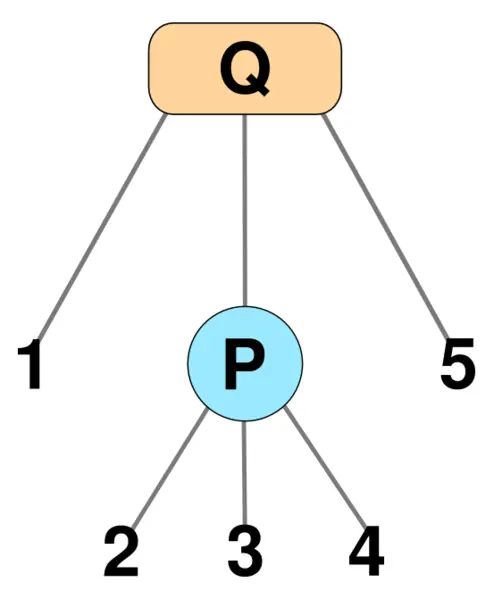
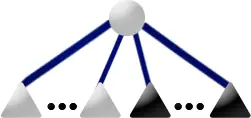
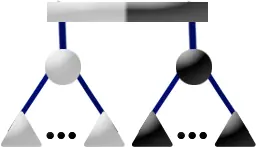
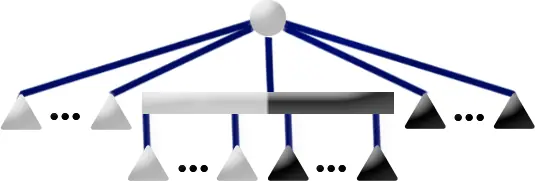
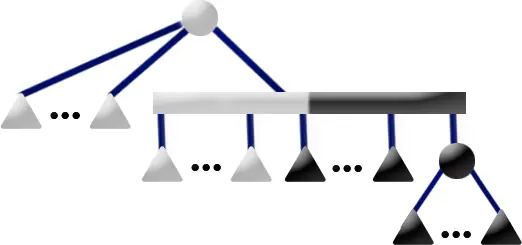
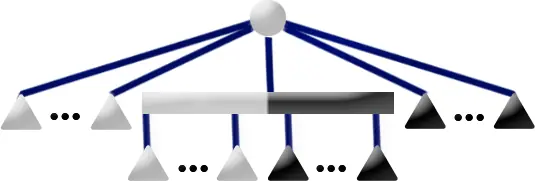
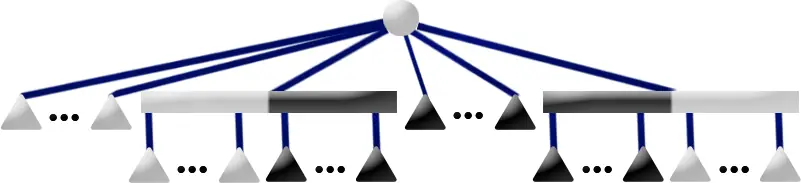
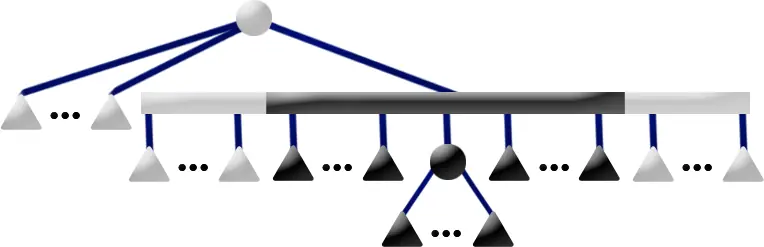
下图是一棵 PQ 树。
其先序遍历 1,2,3,4,5 代表了一个合法方案。如果 P 结点的儿子重排列为 4,2,3,我们得到了另一个合法方案 1,4,2,3,5。保持 P 结点儿子顺序不变,Q 结点的儿子顺序反转,得到了另一个合法方案 5,3,2,4,1。
PQ 树使用儿子 - 兄弟表示法。
我们增量构建一棵 PQ 树。
首先建立一棵树,其根为 P,总共
当加入一个新的限制集合
我们要求 PQ 树中的结点按照颜色排序。
包含所有黑色结点的最小子树被称为 相关子树,相关子树的根(不一定是整棵树的根)被称为 相关根。
添加一个限制的过程被称为 reduction。一次 reduction 分为两个阶段:冒泡阶段和减少阶段。
冒泡阶段只处理相关子树。我们将相关子树中的所有结点标记为黑色或灰色,并为每个结点计算其拥有的相关子结点数量。为了高效地完成这个过程,我们从叶子往根处理相关子树。这需要记录每个点的父亲结点,但在减少阶段一个点的父亲结点经常要被修改。为了在线性时间内构造,只有 P 结点的儿子和 Q 结点的最后一个儿子 始终记录正确的父亲结点。对于 Q 结点的其他儿子,在冒泡阶段用最后一个儿子的父亲更新他们的父亲。
当遇到一个中间的结点时,我们看一下它的兄弟是否已经有合法的父亲结点。如果没有,将其标记为 阻塞 的。如果后面它的兄弟有了合法的父亲,那么修改这个结点的父亲并且取消标记。如果在冒泡阶段结束时,仍然有一段连续的阻塞结点(如下面的情况 Q3),一个没有父结点的“伪结点”成为该块的父结点,并在减少阶段时被去除。
减少阶段用一个队列来处理结点。首先将所有限制内的叶子结点加入队列。每次取出队首的结点
对于每一个结点
将
如果
如果
- 新建一个 P 结点
$f$ 成为所有黑色儿子的根。 - 新建一个 P 结点
$e$ 成为所有白色儿子的根。 - 如果
$e$ (和/或$f$ )只有一个儿子,那么不要新建结点,而是将$e$ (和/或$f$ )直接赋值成那个儿子。 - 将
$u$ 改成 Q 结点并把其儿子设为$e$ 和$f$ ,将其标记为灰色。
注意到根据之前的定义,Q 结点至少有 3 个儿子,因此这里的
如果
如果
- 新建一个 P 结点
$f$ 成为所有黑色儿子的根。 - 新建一个 P 结点
$e$ 成为所有白色儿子的根。 - 如果
$e$ (和/或$f$ )只有一个儿子,那么不要新建结点,而是将$e$ (和/或$f$ )直接赋值成那个儿子。 - 将
$e$ 的兄弟设为$p$ 最后一个白色儿子,然后把$e$ 设为$p$ 的最后一个儿子。 - 将
$f$ 的兄弟设为$p$ 最后一个黑色儿子,然后把$f$ 设为$p$ 的最后一个儿子。
如果
- 新建一个 P 结点
$f$ 成为所有黑色儿子的根。 - 如果
$f$ 只有一个儿子,那么不要新建结点,而是将$f$ 直接赋值成那个儿子。 - 把
$p_1$ 的最后一个黑色儿子的兄弟设为$f$ 。 - 把
$f$ 的兄弟设为$p_2$ 的最后一个黑色儿子。 - 把
$p_2$ 的最后一个儿子设为$p_2$ 的最后一个白色儿子。
如果
如果
- 设
$p_f$ 为$p$ 最后一个黑色儿子,$p_e$ 为$p$ 最后一个白色儿子,$f$ 为$p$ 的黑色兄弟,$e$ 为$p$ 的白色兄弟。 - 将
$f$ 的兄弟设为$p_f$ ,$e$ 的兄弟设为$p_e$ 。 - 如果
$p$ 没有一个白色兄弟或黑色兄弟,将$u$ 的最后一个儿子设成$p$ 的最后一个儿子。 - 删除
$p$ 。
如果
该构建方法是原论文中的,但是实现较为不便。
目前 OI 中的实现大多采用该方法。其实方法类似,下面出现的情况基本都能在上面找到。
注意到根据之前的染色过程,所有黑色和白色的点都已经满足条件,因此我们 只需要处理灰色结点。
- 如果
$u$ 有多于两个灰色儿子,无解。 - 如果
$u$ 只有一个灰色儿子,且没有黑色儿子,递归处理灰色儿子。 - 否则先清空
$u$ 的儿子,然后加入所有的白色儿子。新建一个 Q 结点$q_1$ 并成为$u$ 的儿子。在$q_1$ 中加入所有的灰色儿子。新建一个 P 结点$p$ 作为所有黑色儿子的根,将$p$ 插入$q_1$ 的中间。(对应了自底向上法 P 结点的所有情况。)
注意到我们会要求两个灰色节点白色全在左侧,黑色全在右侧(或相反),因此我们需要实现一个分裂函数 split,可以把这个子树的点分裂成黑白部分,并同时保留分裂成的子树的节点的 所有可能。
- 找到最左边和最右边的非白色节点位置
$l,r$ 。如果$[l+1,r-1]$ 内有非黑色节点,无解。 - 如果没有黑色节点,只有一个灰色节点,递归处理这个灰色节点,否则只需要将
$l$ 和$r$ 位置的节点分裂。
令要分裂的点为
- 如果
$u$ 有至少两个灰色儿子,则无解。 - 否则左边是所有白色儿子,中间递归处理灰色儿子,右边是所有黑色儿子。注意到要保留所有的可能,因此要新建两个 P 结点分别作为白色儿子和黑色儿子的根。(对应自底向上法的 P4 情况。)
- 删除
$u$ 。
如果
- 如果正序和反序都不满足白 - 灰 - 黑,则无解。
- 如果有至少两个灰色儿子,也无解。
- 否则递归分裂灰色儿子即可。
- 删除
$u$ 。
最后把所有多余的结点(只有一个儿子的结点)删除。
class PQTree {
public:
PQTree() {}
void Init(int n) {
n_ = n, rt_ = tot_ = n + 1;
for (int i = 1; i <= n; i++) g_[rt_].emplace_back(i);
}
void Insert(const std::string &s) {
s_ = s;
Dfs0(rt_);
Work(rt_);
while (g_[rt_].size() == 1) rt_ = g_[rt_][0];
Remove(rt_);
}
std::vector<int> ans() {
DfsAns(rt_);
return ans_;
}
~PQTree() {}
private:
int n_, rt_, tot_, pool_[100001], top_, typ_[100001] /* 0-P 1-Q */,
col_[100001] /* 0-black 1-white 2-grey */;
std::vector<int> g_[100001], ans_;
std::string s_;
void Fail() {
std::cout << "NO\n";
std::exit(0);
}
int NewNode(int ty) {
int x = top_ ? pool_[top_--] : ++tot_;
typ_[x] = ty;
return x;
}
void Delete(int u) { g_[u].clear(), pool_[++top_] = u; }
void Dfs0(int u) { // get color of each node
if (u >= 1 && u <= n_) {
col_[u] = s_[u] == '1';
return;
}
bool c0 = false, c1 = false;
for (auto &&v : g_[u]) {
Dfs0(v);
if (col_[v]) c1 = true;
if (col_[v] != 1) c0 = true;
}
if (c0 && !c1)
col_[u] = 0;
else if (!c0 && c1)
col_[u] = 1;
else
col_[u] = 2;
}
bool Check(const std::vector<int> &v) {
int p2 = -1;
for (int i = 0; i < static_cast<int>(v.size()); i++)
if (col_[v[i]] == 2) {
if (p2 != -1) return false;
p2 = i;
}
if (p2 == -1)
for (int i = 0; i < static_cast<int>(v.size()); i++)
if (col_[v[i]]) {
p2 = i;
break;
}
for (int i = 0; i < p2; i++)
if (col_[v[i]]) return false;
for (int i = p2 + 1; i < static_cast<int>(v.size()); i++)
if (col_[v[i]] != 1) return false;
return true;
}
std::vector<int> Split(int u) {
if (col_[u] != 2) return {u};
std::vector<int> ng;
if (typ_[u]) { // Q
if (!Check(g_[u])) {
std::reverse(g_[u].begin(), g_[u].end());
if (!Check(g_[u])) Fail();
}
for (auto &&v : g_[u])
if (col_[v] != 2) {
ng.emplace_back(v);
} else {
auto s = Split(v);
ng.insert(ng.end(), s.begin(), s.end());
}
} else { // P
std::vector<int> son[3];
for (auto &&x : g_[u]) son[col_[x]].emplace_back(x);
if (son[2].size() > 1) Fail();
if (!son[0].empty()) {
int n0 = NewNode(0);
g_[n0] = son[0];
ng.emplace_back(n0);
}
if (!son[2].empty()) {
auto s = Split(son[2][0]);
ng.insert(ng.end(), s.begin(), s.end());
}
if (!son[1].empty()) {
int n1 = NewNode(0);
g_[n1] = son[1];
ng.emplace_back(n1);
}
}
Delete(u);
return ng;
}
void Work(int u) {
if (col_[u] != 2) return;
if (typ_[u]) { // Q
int l = 1e9, r = -1e9;
for (int i = 0; i < static_cast<int>(g_[u].size()); i++)
if (col_[g_[u][i]]) checkmin(l, i), checkmax(r, i);
for (int i = l + 1; i < r; i++)
if (col_[g_[u][i]] != 1) Fail();
if (l == r && col_[g_[u][l]] == 2) {
Work(g_[u][l]);
return;
}
std::vector<int> ng;
for (int i = 0; i < l; i++) ng.emplace_back(g_[u][i]);
auto s = Split(g_[u][l]);
ng.insert(ng.end(), s.begin(), s.end());
for (int i = l + 1; i < r; i++) ng.emplace_back(g_[u][i]);
if (l != r) {
s = Split(g_[u][r]);
std::reverse(s.begin(), s.end());
ng.insert(ng.end(), s.begin(), s.end());
}
for (int i = r + 1; i < static_cast<int>(g_[u].size()); i++)
ng.emplace_back(g_[u][i]);
g_[u] = ng;
} else { // P
std::vector<int> son[3];
for (auto &&x : g_[u]) son[col_[x]].emplace_back(x);
if (son[1].empty() && son[2].size() == 1) {
Work(son[2][0]);
return;
}
g_[u].clear();
if (son[2].size() > 2) Fail();
g_[u] = son[0];
int n1 = NewNode(1);
g_[u].emplace_back(n1);
if (son[2].size() >= 1) {
auto s = Split(son[2][0]);
g_[n1].insert(g_[n1].end(), s.begin(), s.end());
}
if (son[1].size()) {
int n2 = NewNode(0);
g_[n1].emplace_back(n2);
g_[n2] = son[1];
}
if (son[2].size() >= 2) {
auto s = Split(son[2][1]);
std::reverse(s.begin(), s.end());
g_[n1].insert(g_[n1].end(), s.begin(), s.end());
}
}
}
void Remove(int u) { // remove the nodes with only one child
for (auto &&v : g_[u]) {
int tv = v;
while (g_[tv].size() == 1) {
int t = tv;
tv = g_[tv][0];
Delete(t);
}
v = tv, Remove(v);
}
}
void DfsAns(int u) {
if (u >= 1 && u <= n_) {
ans_.emplace_back(u);
return;
}
for (auto &&v : g_[u]) DfsAns(v);
}
} T;- Booth, Kellogg S. & Lueker, George S. (1976)."Testing for the consecutive ones property, interval graphs, and graph planarity using PQ-tree algorithms".Journal of Computer and System Sciences.13(3): 335–379.doi:10.1016/S0022-0000(76)80045-1.
- PQ Tree Algorithm and Consecutive Ones Problem
- CF243E Matrix PQTree - RainAir's Blog