There are many kinds of algorithms. Most of them fall into one of the eight time complexities that will explore in this chapter.
Eight running time complexities you should know
- Constant time: O(1)
- Logarithmic time: O(Log N)
- Linear time: O(N)
- Linearithmic time: O(N LogN)
- Quadratic time: O(N^2)
- Cubic time: O(N^3)
- Exponential time: O(2^N)
- Factorial time: O(N!)
And here is a plot with all of them

Figure 1. CPU operations vs. Algorithm runtime as the input size grows
As you can see, O(1) and O(log n) is very scalable. However, O(n^2) and worst can convert your CPU into a furnace 🔥 for massive inputs.
Let us know more about these eight time complexities
Represented as O(1), it means that regardless of input size , the number of executions is always the same.
Let's see an example
Example: Finding if an array is empty or not.
Let's implement a function that checks whether the given array is empty or not
Another example is adding an element to the begining of a linked list
As you can see in both examples (array and linked list), if the input is a collection of 10 elements or 10M, it would take the same amount of time to execute. You can’t get any more performant than this!
Represented in Big O notation as O(log n). When an algorithm has this running time, it means that as the input size grows, the number of operations grows very slowly. Logarithmic algorithms are very scalable and one such example is binary search.
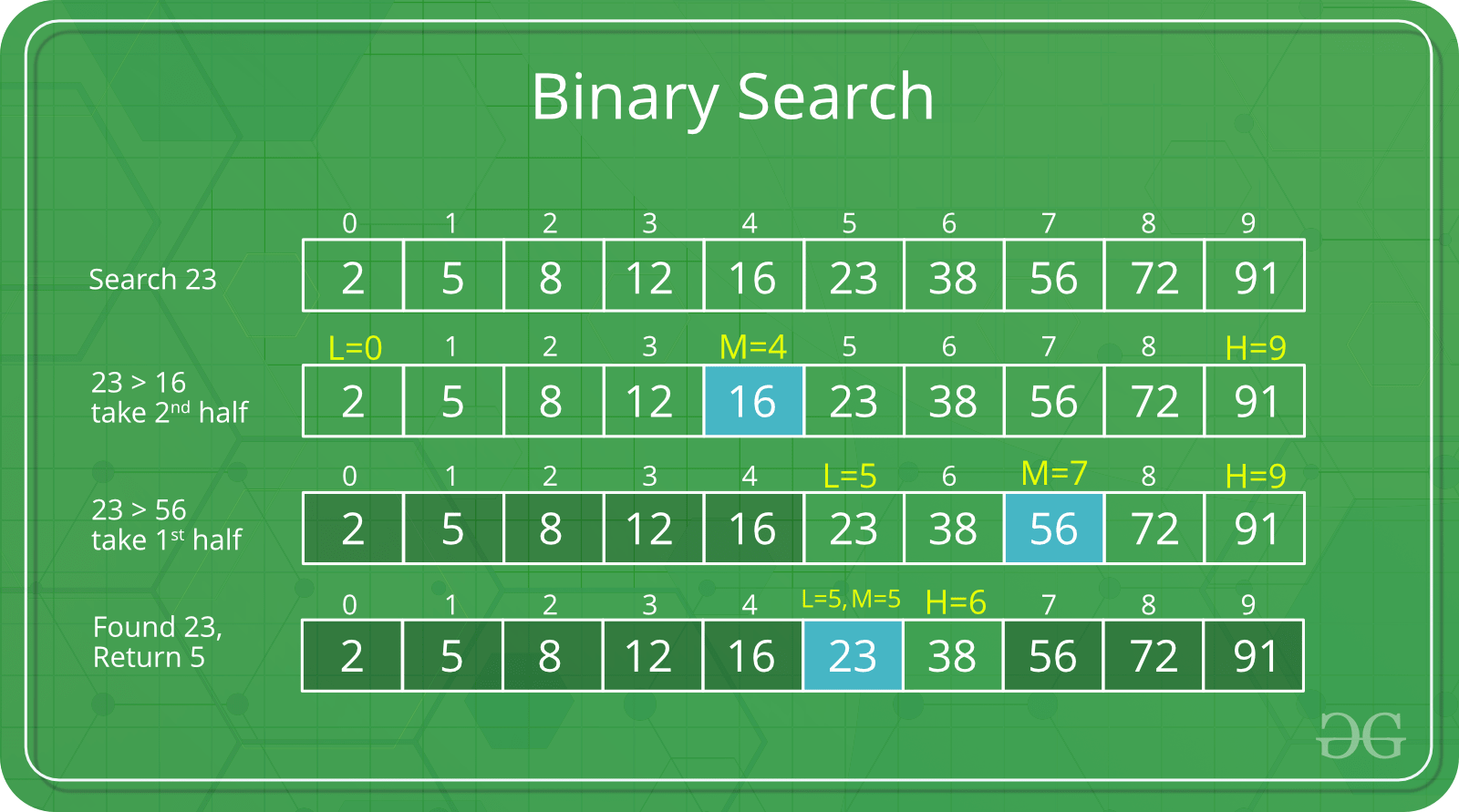
Searching on a sorted array
The binary search only works for sorted arrays. It starts searching for the element in the middle of the array, and then it moves to the right or left depending on if the value you are looking for is larger or smalller.
Binary search
This binary search implementation is a recursive algorithm, which means that the function binarySearchRecursive calls itself multiple times until the program finds a solution. The binary search splits the array in half every time.
Since the binarySearch divides the input in half each time. As a rule of thumb, when you have an algorithm that divides the data in half on each call, you are most likely in front of a logarithmic runtime: O(log n).
Linear algorithms are one of the most common runtimes. Their Big O representation is O(n). Usually, an algorithm has a linear running time when it visits every input element a fixed number of times.
Let’s say that we want to find duplicate elements in an array. What’s the first implementation that comes to mind?
-
Best-case scenario: the first two elements are duplicates. It only has to visit two elements and return.
-
Worst-case scenario: no duplicates or duplicates are the last two. In either case, it has to visit every item in the array.
-
Average-case scenario: duplicates are somewhere in the middle of the collection. As we learned before, the big O cares about the worst-case scenario, where we would have to visit every element on the array. So, we have an O(n) runtime.
You can represent linearithmic algorithms as O(n log n). This one is important because it is the best runtime for sorting! Let’s see the merge-sort.
Sorting elements in an Array
- If the array only has two elements, we can sort them manually.
- We divide the array into two halves.
- Merge the two parts recursively with the merge function explained below
MergeSort.c
The merge function combines two sorted arrays in ascending order. Let’s say that we want to sort the array [9, 2, 5, 1, 7, 6]. In the following illustration, you can see what each function does.

How do we obtain the running time of the merge sort algorithm? The merge-sort divides the array in half each time in the split phase, log n, and the merge function join each splits, n. The total work is O(n log n). There are more formal ways to reach this runtime, like using the Master Method and recursion trees.
Quadratic running times, O(n^2), are the ones to watch out for. They usually don’t scale well when they have a large amount of data to process.
Usually, they have double-nested loops, where each one visits all or most elements in the input. One example of this is a naïve implementation to find duplicate words on an array.
Finding duplicates in an array (naïve approach)
If you remember, we have solved this problem more efficiently in the Linear section. We solved this problem before using an O(n), let’s solve it this time with an O(n^2):
class Solution {
public:
bool containsDuplicate(vector<int>& nums) {
for (int i = 1; i < nums.size(); ++ i) {
for (int j = 0; j < i; ++ j) {
if (nums[i] == nums[j]) {
return true;
}
}
}
return false;
}
};As you can see, we have two nested loops causing the running time to be quadratic. How much difference is there between a linear vs. quadratic algorithm?
Let’s say you want to find a duplicated middle name in a phone directory book of a city of ~1 million people. If you use this quadratic solution, you would have to wait for ~12 days to get an answer 🐢; while if you use the linear solution, you will get the answer in seconds! 🚀
Cubic O(n^3) and higher polynomial functions usually involve many nested loops. An example of a cubic algorithm is a multi-variable equation solver (using brute force) or finding three elements on an array that add up to a given number.
3 SUM
Let’s say you want to find 3 items in an array that add up to a target number. One brute force solution would be to visit every possible combination of 3 elements and add them to see if they are equal to the target.
bool find3Numbers(int A[], int arr_size, int sum)
{
int l, r;
// Fix the first element as A[i]
for (int i = 0; i < arr_size - 2; i++) {
// Fix the second element as A[j]
for (int j = i + 1; j < arr_size - 1; j++) {
// Now look for the third number
for (int k = j + 1; k < arr_size; k++) {
if (A[i] + A[j] + A[k] == sum) {
printf("Triplet is %d, %d, %d",
A[i], A[j], A[k]);
return true;
}
}
}
}
// If we reach here, then no triplet was found
return false;
}As you can see, three nested loops usually translate to O(n^3).
Exponential runtimes, O(2^n), means that every time the input grows by one, the number of operations doubles. Exponential programs are only usable for a tiny number of elements (<100); otherwise, it might not finish in your lifetime. 💀
Let’s do an example.
Finding subsets of a set
Finding all distinct subsets of a given set can be implemented as follows:
#Subsets in a set
// CPP program to find all subsets by backtracking.
#include <bits/stdc++.h>
using namespace std;
// In the array A at every step we have two
// choices for each element either we can
// ignore the element or we can include the
// element in our subset
void subsetsUtil(vector<int>& A, vector<vector<int> >& res,
vector<int>& subset, int index)
{
res.push_back(subset);
for (int i = index; i < A.size(); i++) {
// include the A[i] in subset.
subset.push_back(A[i]);
// move onto the next element.
subsetsUtil(A, res, subset, i + 1);
// exclude the A[i] from subset and triggers
// backtracking.
subset.pop_back();
}
return;
}
// below function returns the subsets of vector A.
vector<vector<int> > subsets(vector<int>& A)
{
vector<int> subset;
vector<vector<int> > res;
// keeps track of current element in vector A;
int index = 0;
subsetsUtil(A, res, subset, index);
return res;
}
// Driver Code.
int main()
{
// find the subsets of below vector.
vector<int> array = { 1, 2, 3 };
// res will store all subsets.
// O(2 ^ (number of elements inside array))
// because at every step we have two choices
// either include or ignore.
vector<vector<int> > res = subsets(array);
// Print result
for (int i = 0; i < res.size(); i++) {
for (int j = 0; j < res[i].size(); j++)
cout << res[i][j] << " ";
cout << endl;
}
return 0;
}- Base case is empty element.
- For each element from the input, append it to the results array.
- The new results array will be what it was before + the duplicated with the appended element. Every time the input grows by one, the resulting array doubles. That’s why it has an O(2n).
The factorial runtime, O(n!), is not scalable at all. Even with input sizes of ~10 elements, it will take a couple of seconds to compute. It’s that slow! 🍯🐝
Factorial:
A factorial is the multiplication of all the numbers less than itself down to 1.
Getting all permutations of a word
One classic example of an O(n!) algorithm is finding all the different words formed with a given set of letters.
This is probably the most trivial example of a function that runs in O(n!) time (where n is the argument to the function):
void nFacRuntimeFunc(int n) {
for(int i=0; i<n; i++) {
nFacRuntimeFunc(n-1);
}
}As you can see in the getPermutations function, the resulting array is the factorial of the word length.
Factorial starts very slow and quickly becomes unmanageable. A word size of just 11 characters would take a couple of hours in most computers! 🤯
We went through 8 of the most common time complexities and provided examples for each of them. Hopefully, this will give you a toolbox to analyze algorithms.