+-
+
算术运算的结果是确定的——会变越来越简单。
+
+-
+
代数运算是没有办法去定义“好”运算的。
+
@@ -1840,14 +1880,16 @@ 为什么算术比代数简单?
算法是一种自动工作的流程,按照小步工作进行自动运算。
比如下面这道题目。
-题目:Problem - B - Codeforces这是 Codeforces 周赛 div2 的一道题目,比较简单,大家可以简单的思考一下
-
+题目:
+Problem - B - Codeforces
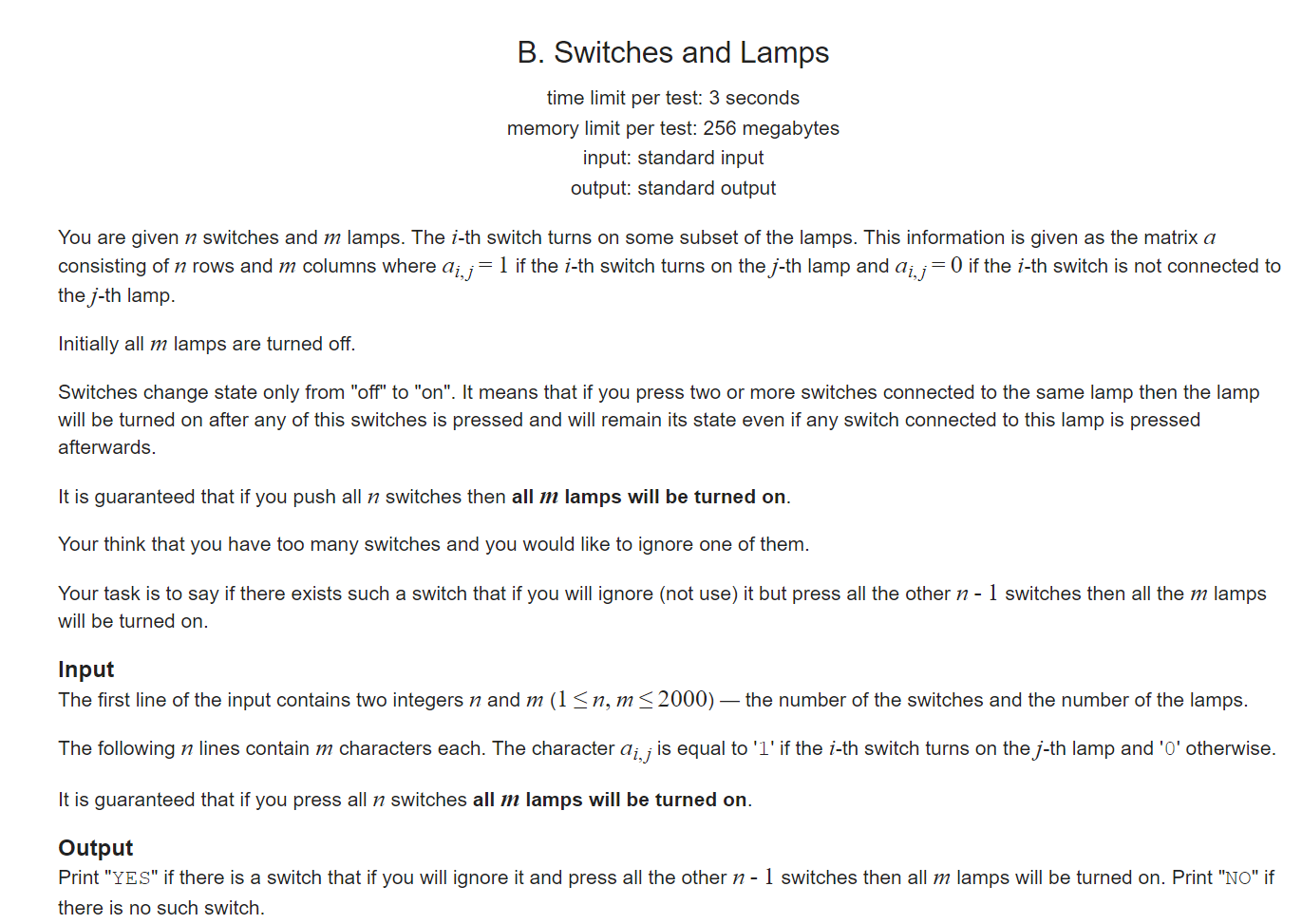
+这是 Codeforces 周赛 div2 的一道题目,比较简单,大家可以简单的思考一下
+
英文看着很长,实际题目很简单,有 n 个开关和 m 盏灯,只要存在一个控制这个灯是开着的这个等就会被点亮。
然后给你 01 矩阵,表示 n 个开关控制 m 盏灯,行列为 1 表示可以让灯亮着,问你能否删掉一个开关,使得所有灯被点亮。
思路想到的很简单,对于每一行求和,如果对于每一行,如果去掉某一行后这一列的和变成 0 ,说明有灯不能删掉,一个简单的枚举法,每一次检测开关的时间复杂度是 \(O(mn)\),所以总的时间复杂度是\(O(mn^2)\),刚好够 \(3s\) 的时间限制。当然,可以用前缀和或者位运算的奇技淫巧进行复杂度降低,这里不进行展开。
那么这个思路从线性代数的角度怎么看呢……
-就是求线性无关组,如果在线性无关组里面就是 NO,如果不在线性无关组里面就是 YES,当然线性无关组在这里是唯一的。
-线性无关组代表没有冗余的信息,这些信息都是线性无关的,也就是向量之间无法用彼此之间相互表达的含义,因此,在题目里,就是检测有没有开关是冗余的。
+就是求线性无关组,如果在线性无关组里面就是 NO,如果不在线性无关组里面就是 YES,当然线性无关组在这里是唯一的。
+线性无关组代表没有冗余的信息,这些信息都是线性无关的,也就是向量之间无法用彼此之间相互表达的含义,因此,在题目里,就是检测有没有开关是冗余的。
源码实现可以参考 Python numpy 里面的 matrix_rank 函数实现。在 \(linalg/\_linalg.py\) 目录下的 \(1973\) 行
@@ -1855,7 +1897,7 @@ 什么是算法
略过基础性的向量加减运算,我们先重新复习一下数乘。
$$
-2\times\begin{bmatrix}1\2\end{bmatrix} = \begin{bmatrix}2\4\end{bmatrix}
+2 \times\begin{bmatrix}1\\2\end{bmatrix} = \begin{bmatrix}2\\4\end{bmatrix}
$$
什么意思,这是一个几何上的伸缩运算,把原来的向量拉伸了 \(2\) 倍,由此引到我们线性变换的内容。
@@ -1871,25 +1913,24 @@ 叉乘的作用
-这里我们计算叉乘通常使用右手系,但是在 UE4 和 OpenGL 中使用的是左手系,问题不大,翻转一下就可以了。
+这有什么作用呢,比如在渲染的时候我可以画一个三角形,然后用向量的叉乘快速判断这个点是不是在三角形内部。(可以扩展到任意凸包,求凸包的相关算法可以用点乘,详情参询https://oi-wiki.org/geometry/convex-hull/)
+
这里我们计算叉乘通常使用右手系,但是在 UE4 和 OpenGL 中使用的是左手系,问题不大,翻转一下就可以了。
向量的叉乘和向量的点乘都可以写成矩阵乘法的形式,可以思考一下怎么个一回事。(提示:伴随矩阵)
真正的变换专场
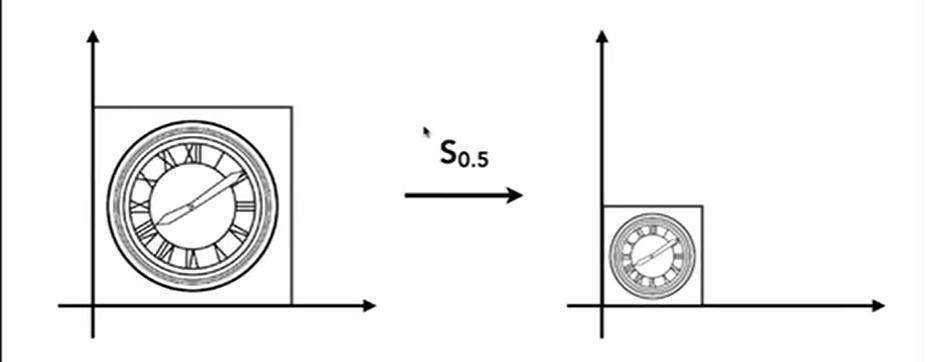
缩放变换
- -横轴和纵轴都变成了原来的 \(\frac{1}{2}\) 用数学的语言表达呢如下
+
-横轴和纵轴都变成了原来的 \(\frac{1}{2}\) 用数学的语言表达呢如下
+

+横轴和纵轴都变成了原来的 \(\frac{1}{2}\) 用数学的语言表达呢如下
$$
x^{'} = sx \quad y^{'} = sy
$$
作为一个学过线性代数的人呢,需要学会把这个转换成为矩阵形式,就比如这个样子
$$
-\begin{bmatrix}x^{'}\y^{'}\end{bmatrix}=\begin{bmatrix}s & 0\0&s\end{bmatrix}\begin{bmatrix}x\ y\end{bmatrix}
-$$
-
+\begin{bmatrix}x^{'}\\y^{'}\end{bmatrix}=\begin{bmatrix}s & 0\\0&s\end{bmatrix}\begin{bmatrix}x\ y\end{bmatrix}
+$$
+
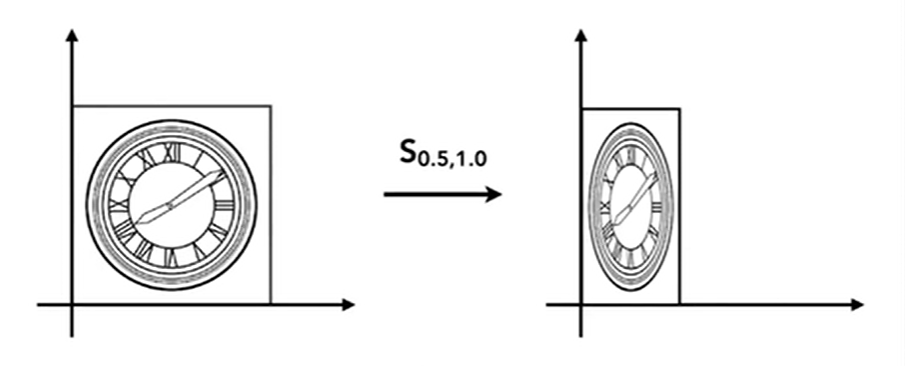
当然,也可以不均匀的缩放,比如 \(x\) 和 \(y\) 一个缩小到 \(\frac{1}{2}\),一个保持不变。
$$
-\begin{bmatrix}x^{'}\y^{'}\end{bmatrix}=\begin{bmatrix}s_x & 0\0&s_y\end{bmatrix}\begin{bmatrix}x\ y\end{bmatrix}
+\begin{bmatrix}x^{'}\\y^{'}\end{bmatrix}=\begin{bmatrix}s_x & 0\\0&s_y\end{bmatrix}\begin{bmatrix}x\ y\end{bmatrix}
$$
对称变换
学过近世代数的同学应该都知道,矩阵运算时非常符合群这个东西的定义的,但是如果从高中数学推导过来呢,群一开始诞生就是为了描述对称性这个东西的。所以矩阵应该是很轻松的就能把对称这个东西给描述出来的。
@@ -1897,26 +1938,26 @@ 对称变换